Анализ нелинейной системы
По заданной структурной схеме системы автоматического управления построить её фазовый портрет методом припасовывания. По фазовому портрету выполнить анализ системы автоматического управления и определить её устойчивость.
|
|
|
|
|
|
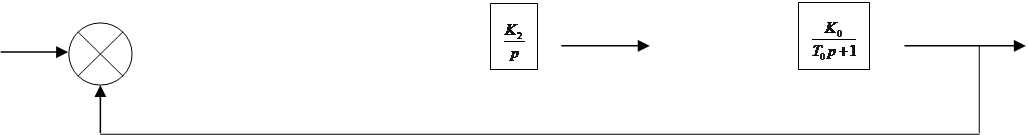 |
|||
 |
|||
![]()
![]()
![]() T0=16 awср=0.5
T0=16 awср=0.5
|
|
|
![]()
|
K2=3.9 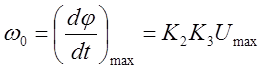
K3=0.008
РЕШЕНИЕ:
1.Преобразование структурной схемы:
Выделим в заданной стуктурной схеме линейную и нелинейную части данной системы:

где 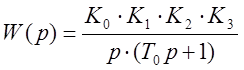 –
эквивалентная передаточная функция всех линейных звеньев системы.
–
эквивалентная передаточная функция всех линейных звеньев системы.
F(Q1-Q2) – эквивалентная статическая характеристика всех нелинейных элементов.
По определению W(p)= Q2/Q3 , следовательно
W(p)· Q3 = Q2;
Q3 = F(Q1-Q2);
Q2 = W(p)·F(Q1-Q2).
преобразуем уравнения учитывая линейную часть:
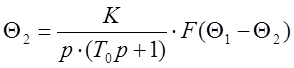 , где K=К0К1К2К3
, где K=К0К1К2К3
![]() .
(1)
.
(1)
Будем считать входное воздействие Q1 системы постоянным(Q1=const). Тогда в уравнении (1) перейдем от величины Q2 к её приращению относительно постоянного воздействия Q1:
Введём обозначение: Q2 - Q1 = x, тогда
px = pQ2 - pQ1;
px = pQ2.
В результате уравнение (1) примет вид:
![]() (2)
(2)
Нелинейная часть системы является трехпозиционным реле, статическая характеристика которого приведена выше. Решение данного уравнения будет строиться исходя из заданной нелинейности:
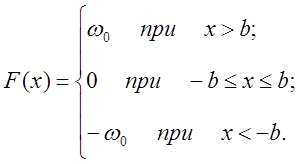 (3)
(3)
В соответствии с системой (3) и учетом того, что функция является нечетной, т.е. симметрична относительно начала координат, уравнение (2) разбивается на систему из трёх уравнений:
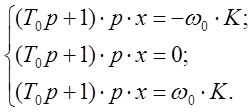 (4)
(4)
Заменим px=V, тогда система (4) приобретет вид:
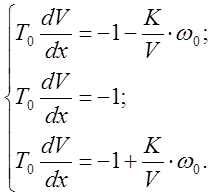 (5)
(5)
Найдем решение каждого из уравнений системы:
1) 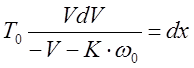 .
.
Т.к. изначально система выведена в точку фазовой плоскости М0 с координатами (x0,V0) , то интегрирование будет: от x0 до x ; от V0 до V.
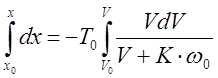
Решив интеграл получим:
![]()
![]()
2) ![]()
![]()
![]() - отрезок прямой для
интервала
- отрезок прямой для
интервала ![]()
3)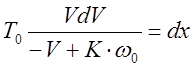
Решение аналогично первому уравнению:
![]()
3.Построение фазового портрета
Построим фазовый портрет по полученным решениям уравнений системы (5):
Пусть первая точка будет M0(1;0,5). Первое уравнение имеет вид:
![]() для x > 0.51
для x > 0.51
Вторая точка будет М1(0,51; -0,37655). Второе уравнение имеет вид:
![]() для x > 0.51
для x > 0.51
Третья точка будет М2(-0,51;-0,31181). Третье уравнение имеет вид:
![]() для –0.51 ≤ x ≤ 0.51
для –0.51 ≤ x ≤ 0.51
Четвертая точка будет М3(-0,51;0,24495), тогда четвертое уравнение имеет вид:
![]() для х < -0.51
для х < -0.51
Пятая точка будет M4(0,51;0,18135). Пятое уравнение имеет вид:
![]() для –0.51 ≤ x ≤ 0.51
для –0.51 ≤ x ≤ 0.51
Шестая точка будет М5(0,51;-0,14653). Шестое уравнение имеет вид:
![]() для x > 0.51
для x > 0.51
Седьмая точка будет M6(-0,51;-0,082306). Седьмое уравнение имеет вид:
![]() для –0.51 ≤ x ≤ 0.51
для –0.51 ≤ x ≤ 0.51
Восьмая точка будет М7(-0,51;0,0767), тогда восьмое уравнение имеет вид:
![]() для х < -0.51
для х < -0.51
Девятая точка будет М8(0,51;0,013), девятое уравнение имеет вид:
![]() для –0.51 ≤ x ≤ 0.51
для –0.51 ≤ x ≤ 0.51
Десятая точка будет М9(0,51;-0,0122), десятое уравнение имеет вид:
![]() для x > 0.51
для x > 0.51
Последнее уравнение пересекает ось абсцисс в интервале (-0,51;0,51) в точке М10(0,31592;0), следовательно, все уравнения для фазового портрета найдены. Это означает что, с этого момента система блуждает с нулевой скоростью и неопределенностью по координате от -0,51 до +0,51, это состояние характерно состоянию устойчивости.
По заданной структурной схеме составим принципиальную схему системы автоматического регулирования температуры:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.