Если: Q0(x)=0 то н.у. (2) называются нулевым
Q0(x)≠0 то н.у. (2) называются ненулевыми
Условие (2) необходимо,
но не достаточно для выделения единственного решения (1) что является
принципиальной особенностью СРП по сравнению с ССП. Полная система соотношений
должна содержать граничные условия для Q(x,t), которая характеризует
взаимодействия Q(x,t) с внешней средой должны выполнятся для t>0 на границе: 
области Д:
Г[Q(x,t)]=g(x,t) 
(3)
где: Г-линейный оператор
g(x,t)-внешнее воздействие которое можно рассматривать как второй вход объекта наряду с f(x,t).
Если: g(x,t)=0, то граничные условия однородные
g(x,t)≠0, то граничные условия неоднородные
Уравнения (1)-(3) с заданными линейными и диф. операторами L,N,Г составляющие краевую задачу является базовой моделью для мат. описания широкого класса ОРП. Для простейшего случая пространственная распределенность Q(x,t) изменяющиеся на отрезке [х0,х1] по одной координате х (однородная задача) уравнения запишется следующим образом:
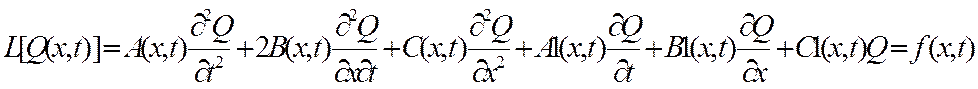
Где: А,В,С,А1,В1,С1-заданные функции как правило постоянные.
В зависимости от дискриминанта Δ=АС-В2 различают следующие классы уравнения:
- Δ<0 уравнения гиперболического типа
- Δ=0 уравнения параболического типа
- Δ>0 уравнения эллиптического типа
- смешанная задача Δ меняет знак в области допустимых значений x и t.
В общем случае описание функции состояния (Q(x,t)) СРП может, не сводится к перечисленным выше уравнениям так как:
- оператор L может быть нелинейным
- уравнения могут быть многомерными
- порядок уравнения может быть больше второго (порядок уравнения соответствует порядку наивысшей производной)
- поведения СРП может моделироваться не одним, а системой уравнений в частных производных, то есть описываться векторным уравнением.
2.2 Представление колокольного дифманометра в виде элементарных блоков
Структурная схема колокольного дифманометра имеет вид:
СРП ССП ССП ССП
Р’, Па Р’’, Па l, м L, Гн I, A
Р’, Па – измеряемое давление;
Р’’, Па – разность между Р’ и атмосферным давлением;
l, м- перемещение колокола;
L, Гн – индуктивность катушки индукционного преобразователя;
I, А – токовый выходной сигнал.
В качестве блока с распределенными параметрами принимаем емкость. Гидростатическое давление жидкости в каждой точке емкости является величиной непостоянной в зависимости от расстояния до поверхности жидкости.
2.3 Выбор и идентификация уравнения
Дифференциальное уравнение, описывающее данную СРП (емкость с жидкостью), относится к параболическому типу.
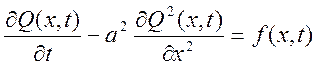
Выходным параметром Q(x, t) является перемещение колокола.
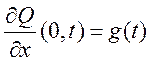Входным воздействием f(x, t) является давление жидкости,
распределенное в емкости, где х – одномерная переменная в декартовых
координатах; t – время.
Начальные условия: Q(x, 0) = Q0(x),
Q0(x), g(t) – значение функции и ее производной.
Граничные условия: 0 ≤ x ≤ , t ≥ 0.
Вводится стандартизирующая функция:
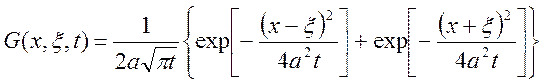Функция Грина:
где - координата точки;
- функция по времени.
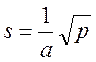
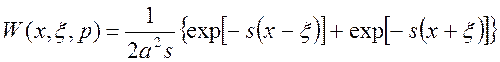Континуальная передаточная
функция:
, где
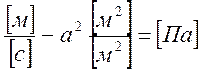Соответствие между размерностями входного и
выходного сигнала в дифференциальном уравнении достигается путем подбора
размерности коэффициента a.
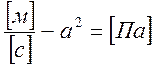
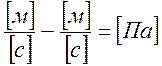
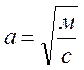
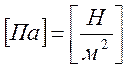Принимаем , тогда
, тогда
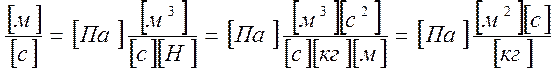
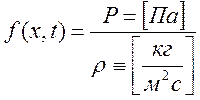, где ρ – поверхностная
плотность.
Зададим входное воздействие:
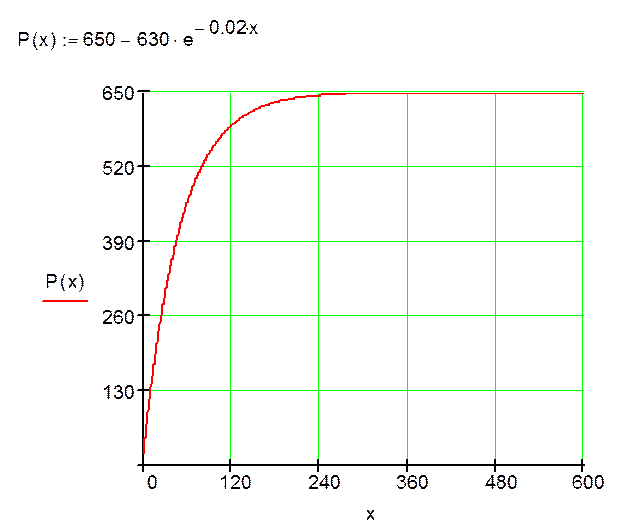
Примем начальные условия:
Q0(x) = 20, что соответствует давлению жидкости у поверхности.
Граничные условия:
g(t) = 650, что соответствует максимальному давлению жидкости в емкости.
3 РАСЧЕТ ВЫХОДНОЙ ВЕЛИЧИНЫ
Для определения вида статической характеристики воспользуемся функцией Грина:
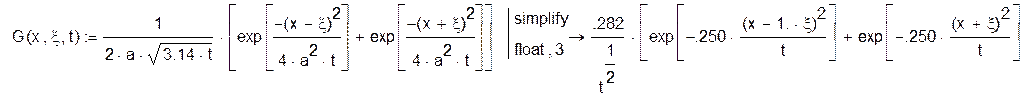
Стандартизирующая функция:
Вычислим двойной интеграл по времени и пространственной области от произведения функции Грина на стандартизирующую функцию. Интеграл двойной, так как задача является двумерной (давление жидкости распределяется расстоянию до поверхности и в каждой точке поперечного сечения одинаково).
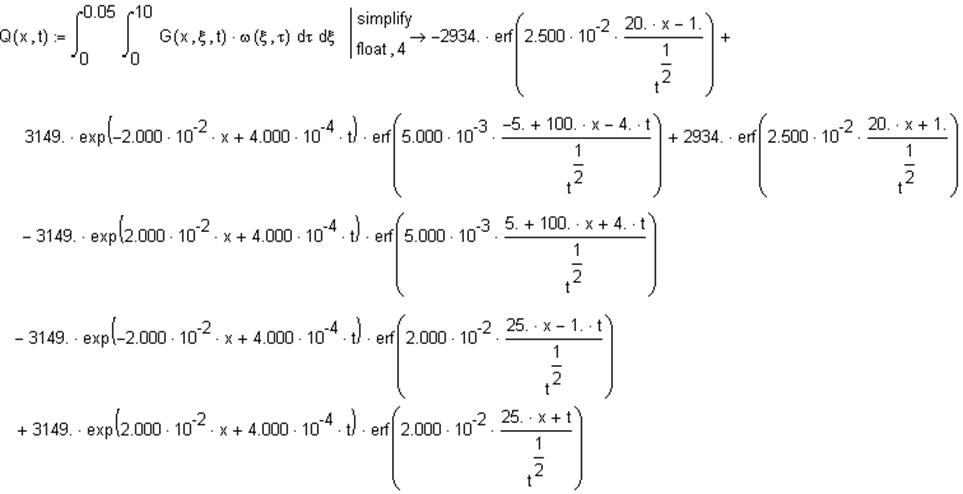
Построим графики зависимостей статической характеристики выходной величины при фиксированных значениях координат и времени:
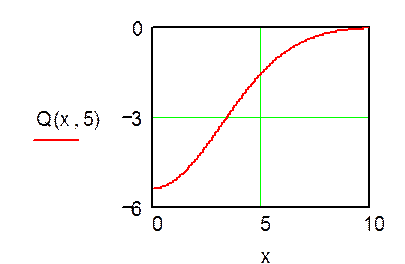
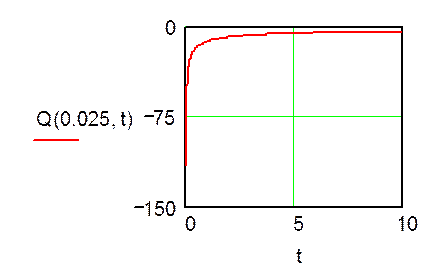
4 РАСЧЕТ ИНТЕГРАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
Найдем преобразование Лапласа от стандартизирующей функции:
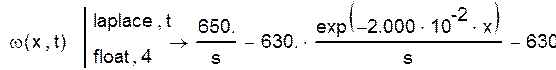
Выделяем входное воздействие:
|
|
|
|
Континуальная передаточная функция:
Найдем интегральную передаточную функцию как интеграл по пространственной области от произведения континуальной передаточной функции на остаток стандартизирующей функции, найденный ранее.
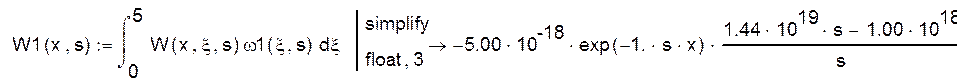
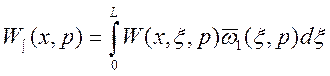
При конкретных значениях:
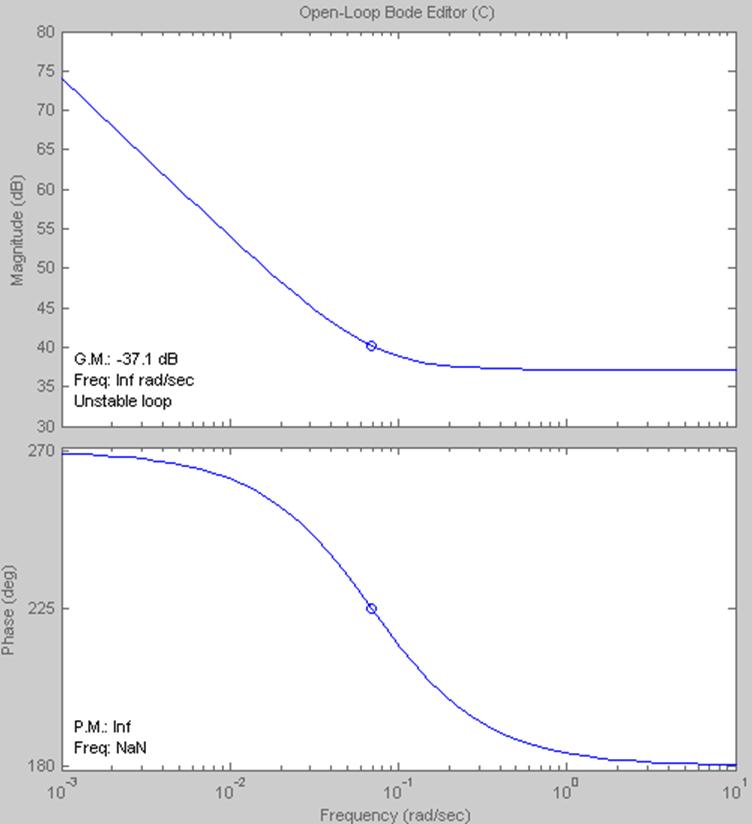
5 ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК. СИНТЕЗ АПРОКСИМИРОВАННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
Для построения логарифмических характеристик воспользуемся приложением sisotool программной среды Matlab, создав zpk – объект для интегральной передаточной функции.
20lgK
- 40
+ 40
wСР
Определим частоту среза, представив передаточную функцию в виде произведения стандартных звеньев.
20lgK = 74, K = 5012.
wср = 0,1 с-1, Т = 10 с.
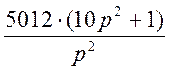
W(p) = .
ЗАКЛЮЧЕНИЕ
В данной курсовой работе была проанализирована конструкция колокольного дифманометра, построена его структурная схема и представлена в виде системы с распределенными параметрами. Для полученной СРП был произведен синтез интегральной передаточной функции. В ходе расчетов было выявлено, что система неустойчива.
В целом на практике была изучена методика исследования системы с распределенными параметрами.
СПИСОК ЛИТЕРАТУРЫ
1. Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. М., Наука, 1975. 767с.
2. Бутковский А.Г. Системы с распределенными параметрами. Спра вочник М.Наука-79г.
3. Кремлевский П.П. Дифманометры. Изд. 3-е, переработ. и доп. Л.: Машиностроение, 1975. – 776 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
