Кроме того, колокольные дифманометры находят широкое применение при измерении и регулировании давления в мартеновских, стеклоплавильных и других печах.
Рабочая жидкость в колокольных приборах не должна иметь склонность ни к испарению, ни к поглощению влаги из газа. Такими свойствами обладает ртуть и масла, особенно парафинистые.
1.2 Динамические характеристики
На рис. 2 дано схематическое изображение наиболее общего случая двухжидкостного колокольного дифманометра с криволенейным профилем как стенок колокола, так и его плунжера.
Ф
 |
FH
f0 F
fx FX
b1 b1
c
b a f1x c a b
a1 a1
dz
c1 c1
PЛ РТ
f2
S
Рис. 2 Схема двухжидкостного колокольного дифманометра с криволинейным плунжером и криволинейными стенками
Введем обозначения: FH - наружная площадь колокола; F – внутренняя площадь дна колокола (с плунжером); f0 – площадь поперечного сечения стенок колокола в верхней цилиндрической части; FX – внутренняя площадь колокола в сечении а-а; Ф – площадь большого сосуда; s – наружная площадь малого сосуда; f2 – внутренняя площадь малого сосуда; f1x – площадь поперечного сечения плунжера в сечении с-с, совпадающем с плоскостью зеркала жидкости в малом сосуде; ρЛ – плотность жидкости (легкой) в большом сосуде; ρТ - плотность жидкости (тяжелой) в малом сосуде; ρ – плотность среды, находящейся над жидкостями, залитыми в сосуд; h – разность уровней жидкости снаружи и внутри колокола.
Положение уровней жидкости при данной величине перепада давления p1-p2 изображается: внутри колокола – линией а-а, снаружи колокола – линией b-b и внутри малого сосуда – линией с-с.
Дадим некоторое приращение перепаду давления d(p1-p2). Допустим, что при этом колокол поднимается на величину dH, уровень внутри колокола опустится на величину dy и перейдет в сечение а1-а1, уровень внутри малого сосуда опуститься на величину dz и перейдет в сечение с1-с1, а уровень снаружи колокола поднимется на величину dx и перейдет из сечения b-b в сечение b1-b1.
Приравняем друг другу происшедшие при этом изменения подъемной силы от перепада давления и гидростатического давления жидкости на колокол:
d(p1-p2)FH = (dH + dy)fxg(ρЛ – ρ) + (dH + dz) f1g(ρT – ρ)
Решая это уравнение совместно с уравнениями равенства объемов
dy(FX – s) = dHfx + dx(Ф – FH);
dz(f2 – f1x) = dHf1x
и имея в виду, что
d(p1-p2) = dhg(ρЛ – ρ);
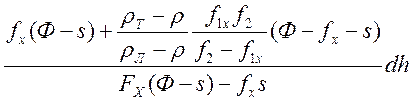dh = dx + dy,
получим
d(p1-p2) = g(ρЛ – ρ)
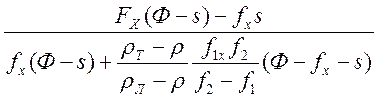Отсюда
dH = dh ,
и уравнение для перемещения уровня жидкости снаружи колокола:
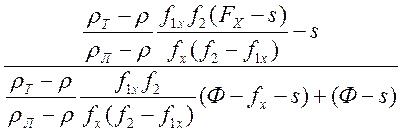
dx = dh .
В данном уравнении все величины, кроме х и h, постоянные (конструктивные и технологические параметры), поэтому передаточная функция колокольного дифманометра будет иметь вид:
W = k – усилительное звено.
где k будет:
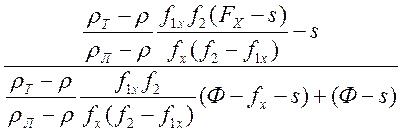
k = .
Найдем численное значение передаточной функции на основе технических характеристик:
ρТ = 1300 кг/м3;
ρЛ = 1000 кг/м3;
ρ = 0,005 кг/м3;
f1x = 0,38*10-4 м2;
f2 = 0,11*10-3 м2;
fХ = 0,45*10-3 м2;
Fх = 0,75*10-3 м2;
s = 0,19*10-3 м2;
Ф = 0,18*10-2 м2;
Отсюда W = 5.324*10^-2.
2 МОДЕЛИРОВАНЕИ КОЛОКОЛЬНОГО ДИФМАНОМЕТРА НА МИКРОУРОВНЕ
2.1 Основные понятия СРП
2.1.1 Особенности систем с распределенными параметрами.
Первым этапом в развитии ТАУ был связан с управлениями системами состояния, которых характеризуются поведением во времени t некоторого набора конечного числа n функций одной переменной t:
Q(t)=(Q1(t),Q2(t),…..Qn(t))
Подобные системы обычно описываются обыкновенными диф. Уравнениями (одним или несколькими) относительно Q(t) и называются системами с ССП. Модели большого числа объектов управления ОУ могут быть с достаточной для практических целей точностью отнесены к классу ССП но на практике любой технический ОУ имеет вполне определенные геометрические размеры. Поэтому функция характеризующая его состояния изменяется в пределах пространственной области занимаемой объектом и следовательно зависит не только от времени но и от вектора x пространственных координат являясь функцией Q(x,y) по меньшей мере двух координат. Системы состояния, которых описывается функциями нескольких аргументов, зависящими как от времени, так и от пространственных координат получили название СРП.
2.1.2 Базовое уравнение объектов с распределенными параметрами.
Функция состояния Q(x,t) объекта с
распределенными параметрами ОРП, определенная по пространственной переменной: x 
, удовлетворяет уравнению:
L[Q(x,t)]=f(x,t) x
t>0 (1)
где: Д- открытая часть
области 
не содержащая границы
L-некоторый заданный оператор (линейная функция Q частных производных от Q по x и t различных порядков, интегральный оператор от Q по x и t , или просто x и t).
f(x,t)-известная функция характеризующая внешнее воздействие на процесс.
Если f(x,t)=0 то уравнения (1) однородное
f(x,t)≠0 то уравнения (1) неоднородное
Обычно f(x,t)-вход, а Q(x,t)-выход.
Замечание: далее будем считать, что ОРП описывается единственным уравнением (1) для одной функции Q(x,t).
Для получения единственного решения уравнения (1) необходимо дополнить н.у. которые описываются некоторым линейным оператором:
N[Q(x,t)]= Q0(x), x , t=0 (2)
Уравнение (2) при
заданной начальной функции Q0(x), описывает распределения по всей области 
состояния ОРП в начальный момент
времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.