Понятие о нелинейных системах автоматического регулирования

Элементы теории нелинейных САР

Введение

Понятие о нелинейных системах автоматического регулирования (НСАР)

К нелинейным относятся системы, которые не могут быть описаны в динамике линейными дифференциальными уравнениями. Нелинейность САР является следствием наличия в ней нелинейных звеньев, т.е. звеньев с нелинейными статическими характеристиками.

Нелинейные уравнения весьма разнообразны. Например, уравнения в которых величины и их производные входят не в первой степени, т.е. нелинейно. Уравнение нелинейно также, если коэффициенты уравнения являются функциями амплитуды входного сигнала.

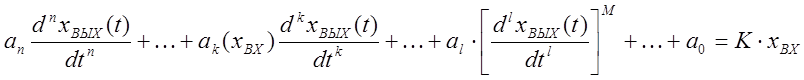
Кроме того, в процессе работы САР, коэффициенты уравнения, описывающие эту работу, могут меняться во времени. Это тоже нелинейные уравнения. Система описанная такими уравнениями носит название нестационарной.

При исследовании нелинейной системы последнюю представляют в виде соединения двух частей: линейной части (Л.Ч.), описываемой  обыкновенным линейным дифференциальным уравнением с постоянными коэффициентами, и нелинейного элемента (Н.Э.) (см. Рис. 1)

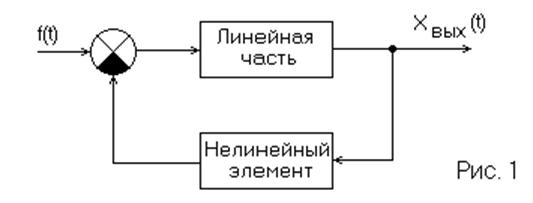
Нелинейный элемент является инерционным и его входная и выходная величины связаны между собой нелинейными алгебраическими характеристиками.

НСАР может содержать одну или несколько нелинейностей.

Если система содержит несколько нелинейностей (нелинейных элементов), то её в некоторых случаях можно свести к рассматриваемому классу, заменив нелинейные элементы одним с результирующей статической характеристикой. (Если, при этом, между нелинейными звеньями имеются разделяющие их инерционные звенья, то систему не удаётся свести к рассматриваемому классу.)

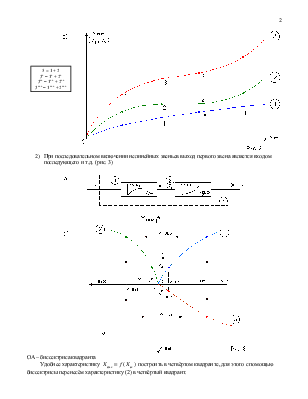
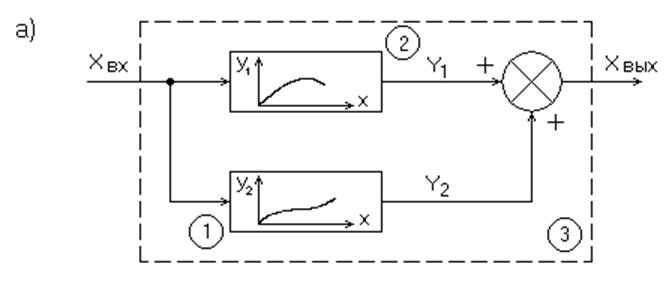
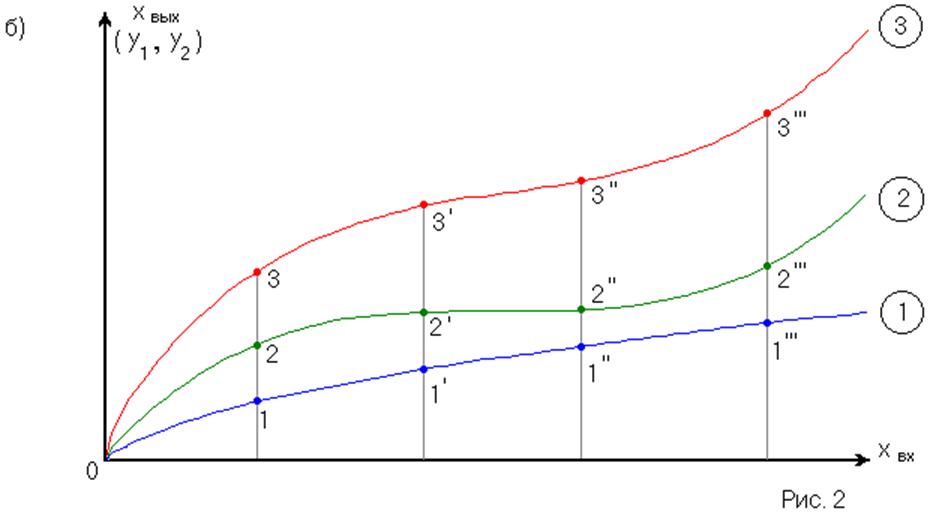
1)  Замена параллельного соединения нелинейных звеньев эквивалентным звеном, статическая характеристика которого может быть получена графическим сложением статических характеристик нелинейных звеньев, включённых параллельно. (рис. 2)

3 = 1 + 2 3’ = 1’ + 2’ 3’’ = 1’’ + 2’’ 3’’’ = 1’’’ + 2’’’

2)  При последовательном включении нелинейных звеньев выход первого звена является входом последующего и т.д. (рис. 3)

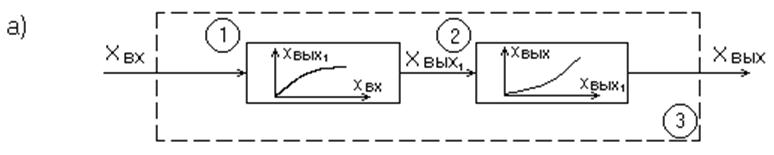
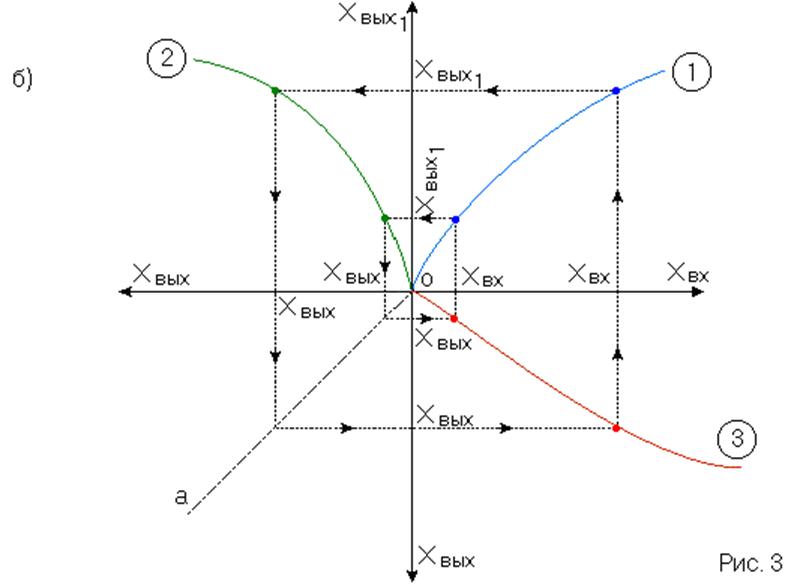
ОА – биссектриса квадранта

Удобнее характеристику  построить в четвёртом квадранте, для этого с помощью биссектрисы перенесём характеристику (2) в четвёртый квадрант.

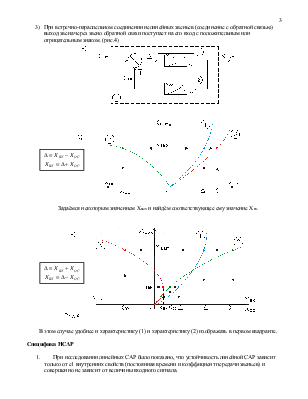
3)  При встречно-параллельном соединении нелинейных звеньев (соединение с обратной связью) выход звена через звено обратной связи поступает на его вход с положительным или отрицательным знаком. (рис.4)

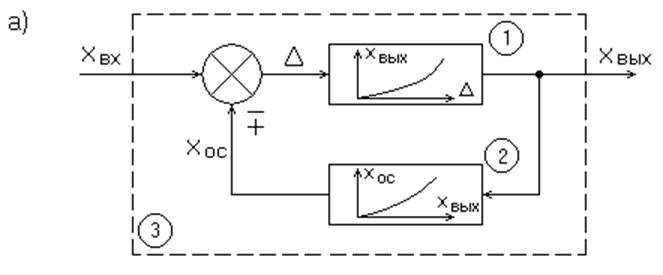
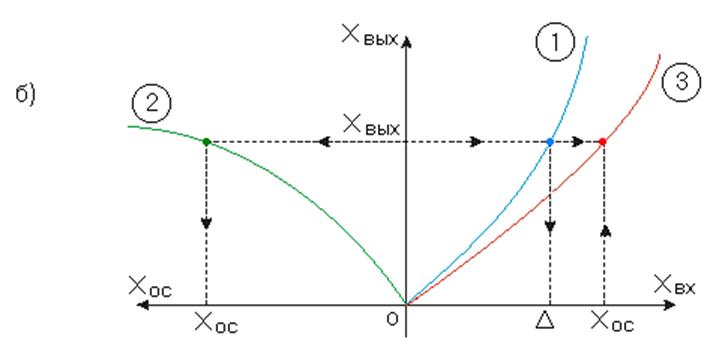
Задаёмся некоторым значением X_вых и найдём соответствующее ему значение X_вх.

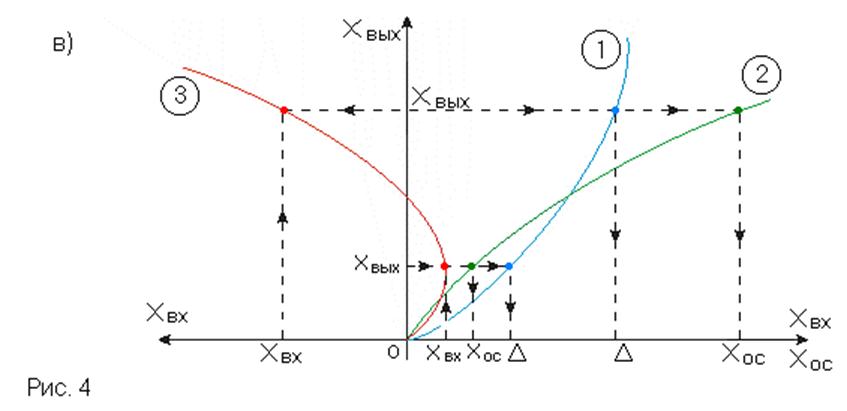
В этом случае удобнее и характеристику (1) и характеристику (2) изображать в первом квадранте.

Специфика НСАР

1.  При исследовании линейных САР было показано, что устойчивость линейной САР зависит только от е1 внутренних свойств (постоянная времени и коэффициент передачи звеньев) и совершенно не зависит от величины входного сигнала.

2.  К линейным системам применим принцип суперпозиции (наложения), гласящий, что если входной сигнал представляет сумму некоторых составляющих, то выходной сигнал можно представить в виде суммы реакций на эти составляющие.
Для НСАР этот принцип (суперпозиции) неприменим, т.к. изменение входного сигнала вызывает непропорциональное изменение выходного сигнала.

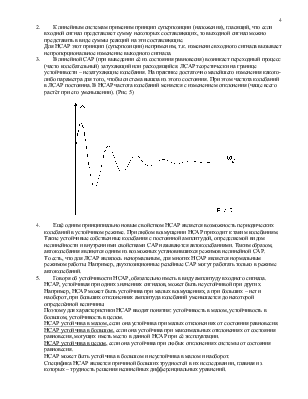
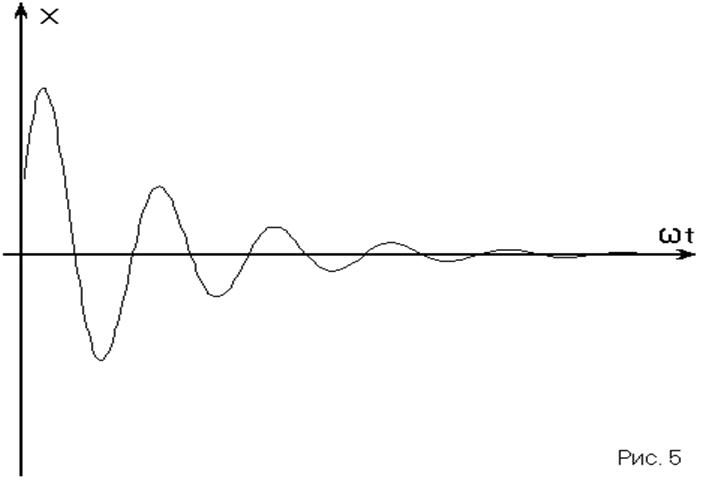
3.  В линейной САР (при выведении её из состояния равновесия) возникает переходный процесс (часто колебательный) затухающий или расходящийся. ЛСАР теоретически на границе устойчивости – незатухающие колебания. На практике достаточно малейшего изменения какого-либо параметра для того, чтобы система вышла из этого состояния. При этом частота колебаний в ЛСАР постоянна. В НСАР частота колебаний меняется с изменением отклонения (чаще всего растёт при его уменьшении). (Рис. 5)

4.  Ещё одним принципиально новым свойством НСАР является возможность периодических колебаний в устойчивом режиме. При любом возмущении НСАР приходит к таким колебаниям.
Такие устойчивые собственные колебания с постоянной амплитудой, определяемой видом нелинейности и внутренними свойствами САР называются автоколебаниями. Таким образом, автоколебания являются одним из возможных установившихся режимов нелинейной САР.
То есть, что для ЛСАР являлось ненормальным, для многих НСАР является нормальным режимом работы. Например, двухпозиционные релейные САР могут работать только в режиме автоколебаний.

5.  Говоря об устойчивости НСАР, обязательно иметь в виду амплитуду входного сигнала. НСАР, устойчивая при одних значениях сигналов, может быть неустойчивой при других.
Например, НСАР может быть устойчива при малых возмущениях, а при больших – нет и наоборот, при больших отклонениях амплитуда колебаний уменьшается до некоторой определённой величины.
Поэтому для характеристики НСАР вводят понятия: устойчивость в малом, устойчивость в большом, устойчивость в целом.
НСАР устойчива в малом, если она устойчива при малых отклонениях от состояния равновесия.
НСАР устойчива в большом, если она устойчива при максимальных отклонениях от состояния равновесия, могущих иметь место в данной НСАР при её эксплуатации.
НСАР устойчива в целом, если она устойчива при любых отклонениях системы от состояния равновесия.
НСАР может быть устойчива в большом и неустойчива в малом и наоборот.
Специфика НСАР является причиной больших трудностей в их исследовании, главная из которых – трудность решения нелинейных дифференциальных уравнений.

II.  Типовые нелинейности

Способ исследования НСАР в значительной степени определяется характером нелинейности. Встречающиеся в САР нелинейности можно разделить на два основных класса: несущественно нелинейные и существенно нелинейные.
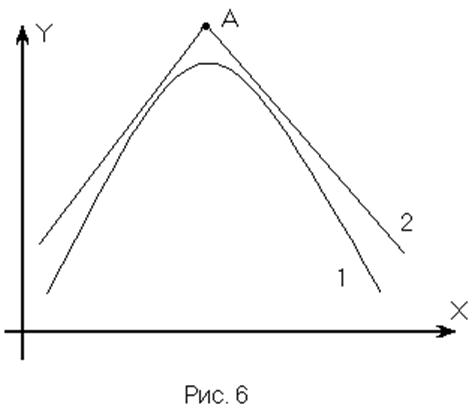
Будем называть нелинейность несущественной, если нелинейная функция и её первая, вторая и т.д. производные непрерывны во всём диапазоне изменения входного сигнала (см. Рис. 6 кривая 1).
Нелинейные звенья, не удовлетворяющие этим требованиям, называются существенно нелинейными.

К несущественным нелинейностям относятся аналитические нелинейности (sin, cos, степенные функции), неаналитические, непрерывные нелинейности (например, кривая намагничивания, механические характеристики двигателя)

Типичные существенные нелинейности:

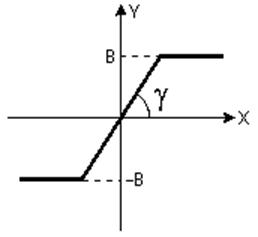
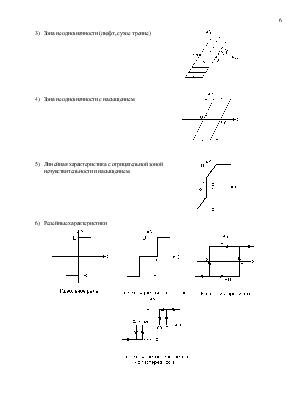
1)  Линейная характеристика с насыщением

 

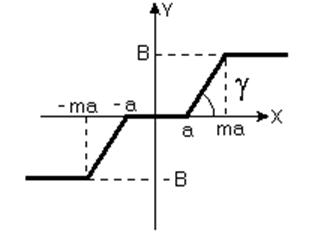
2)  Линейная характеристика с насыщением и зоной нечувствительности

 

3) 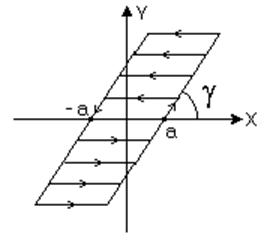 Зона неоднозначности (люфт, сухое трение)

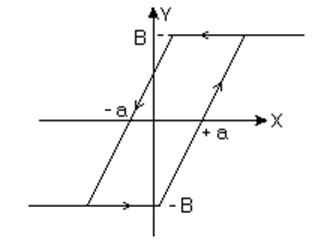
4)  Зона неоднозначности с насыщением

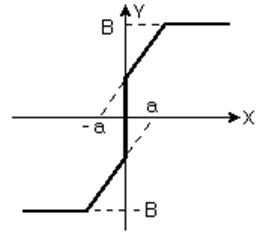
5)  Линейная характеристика с отрицательной зоной нечувствительности и насыщением.

6)  Релейные характеристики

III. Методы исследования НСАР

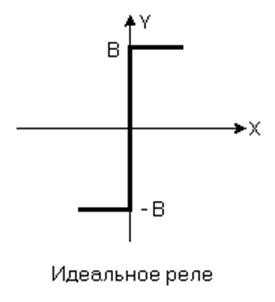
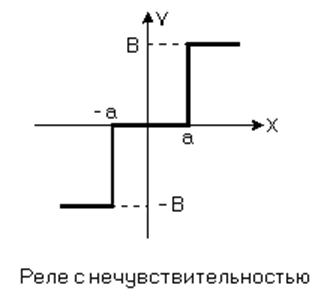
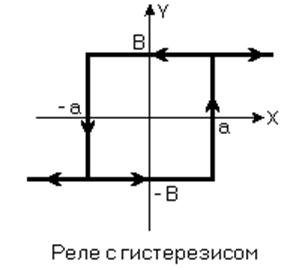
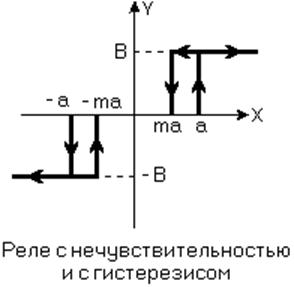
Методы исследования следует разбить на точные и приближённые. Совершенно точно можно исследовать систему только с нелинейностью, составленной из отрезком прямой линии. Точные методы исследования основаны на методе припасовывания. Метод заключается в следующем: поскольку нелинейность состоит из отдельных линейных участков, нелинейное уравнение САР может быть заменено системой линейных дифференциальных уравнений, каждое из которых справедливо для одного участка. Определяется решение для каждого участка в отдельности, а затем эти решения «припасовываются» или «схватываются». Начальными условиями для каждого последующего интервала являются конечные условия для предыдущего интервала. Для дифференциальных уравнений высоких порядков этот метод громоздок и трудоёмок.

Отметим ещё, что точное решение уравнения с любой нелинейностью может быть получено методом математического моделирования на ЭВМ.

Во всех остальных случаях пользуются приближёнными методами. Способа точного решения нелинейного дифференциального уравнения нет, поэтому все приближённые методы сводятся к замене нелинейного уравнения линейным. Эта операция называется линеаризацией (Линеаризация – это замена нелинейного звена эквивалентным ему линейным с сохранением основных свойств нелинейного звена). Далее линеаризованное уравнение исследуется обычными методами линейной теории управления. Применяются два основных способов линеаризации:

1)  для несущественных нелинейностей – статическая линеаризация (разложением в ряд Тейлора)

2)  для существенных нелинейностей – гармоническая (разложением в ряд Фурье).

В случае воздействия на САР случайных сигналов применяют статическую линеаризацию.