Переходные процессы в электрических цепях

     БАЛАКОВСКИЙ   ИНСТИТУТ   ТЕХНИКИ,  ТЕХНОЛОГИИ   И   УПРАВЛЕНИЯ

ФАКУЛЬТЕТ   ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА  ОБЩЕЙ ФИЗИКИ И ЭЛЕКТРОТЕХНИКИ

        ЛАБОРАТОРНАЯ РАБОТА №4

по   дисциплине   Общая электротехника

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В  ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

                                                                   Выполнил   ст. гр.  УИТ-22

                                                                   Волков А.А.

                Принял    ассистент                          

                                                                              Олькова В.Б.  ____________

                                                                    «____» _____________2002г.

2002

Цель работы: Научиться снимать осциллограмму заряда и разряда конденсатора, обрабатывать её, а также проводить необходимые расчеты, связанные с переходными процессами, протекающими в электрических цепях. Требуется также определить ёмкость исследуемого конденсатора.

Приборы и материалы: осциллограф, установка, состоящая из разрядных и зарядных сопротивлений, поляризованного реле, катушки индуктивности, источника ЭДС и конденсатора, емкость которого требуется определить.

Ход работы:

Rзар 1

~

Соберем следующую схему:

 

Рис 1

По условию нам заданы следующие данные:

Таблица 1.Данные необходимые для расчета (по заданию преподавателя):

Rзар, Ом	Rразр , Ом	L, Гн	E, В
5100	51	0,15	10

При помощи прозрачной пленки снимем осциллограмму.

Переходный процесс сводится к решению 2 задач: заряд и разряд конденсатора.

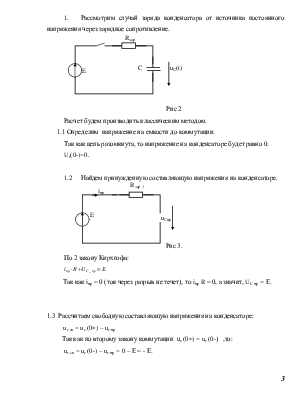
1. 

Rзар

Рассмотрим случай заряда конденсатора от источника постоянного напряжения через зарядное сопротивление.

 

Рис 2

Расчет будем производить классическим методом.

      1.1 Определим  напряжение на емкости до коммутации.

Так как цепь разомкнута, то напряжение на конденсаторе будет равно 0.

U_c(0-)=0.

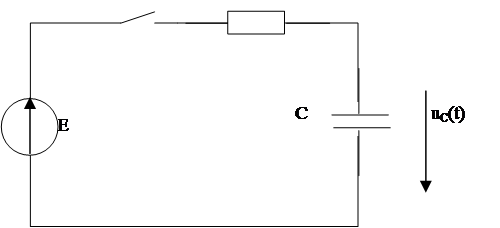
1.2 

Rзар 1

Найдем принужденную составляющую напряжения на конденсаторе.

 

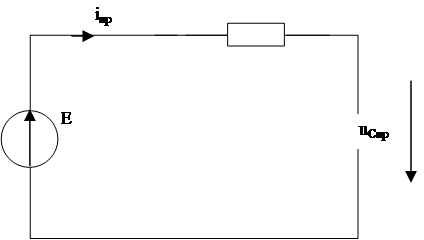Рис 3.

По 2 закону Кирхгофа:

          Так как i_пр = 0 (ток через разрыв не течет), то i_пр R = 0, а значит, U_{C пр} = Е.

1.3  Рассчитаем свободную составляющую напряжения на конденсаторе:

          u_{c св} = u_c (0+) – u_{c пр}

         Так как по второму закону коммутации  u_c (0+) = u_c (0-)   ,то:

u_{c св} = u_c (0-) – u_{c пр} = 0 – Е = - Е.

Подставляя численное значение Е из таблицы 1, получим, что  u_{c св} = - 10 (В).

1.4 Составим характеристическое уравнение.

          Закоротим в схеме источник ЭДС, разорвем цепь в любом месте и определим входное сопротивление относительно этих зажимов:

 

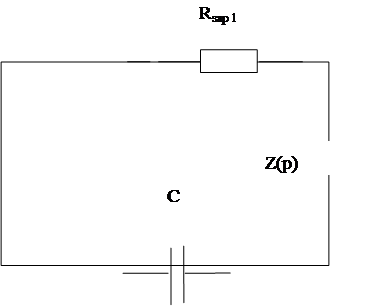Рис 4.

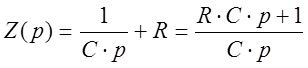                  (1)

Здесь мы учли, что ,

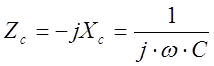
Приравняв к 0 равенство (1), получим характеристическое уравнение:

Решим его: .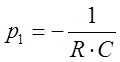

При единственном корне, решение для свободной составляющей записывается в виде: .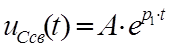

Перепишем это решение для момента времени t=0:

       Так как   , то

А= - Е, значит: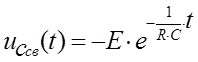

Общее решение найдем как сумму принуждающей и свободной составляющих, то есть:

Общее решение записывается в виде U_C(t)=U_{C пр}+U_{C св}(t)= 10-10e^-196t

u_{c пр} не зависит от t, значит его значение будет постоянным.

Задаваясь моментами времени t, построим график U_C(t)

t	UC пр	UC св(t)	UC(t)
0	10	-10	0
0.002		-6.76	3.24
0.004		-4.57	5.43
0.006		-3	7
0.008		-2	8
0.01		-1.4	8.6

                                           

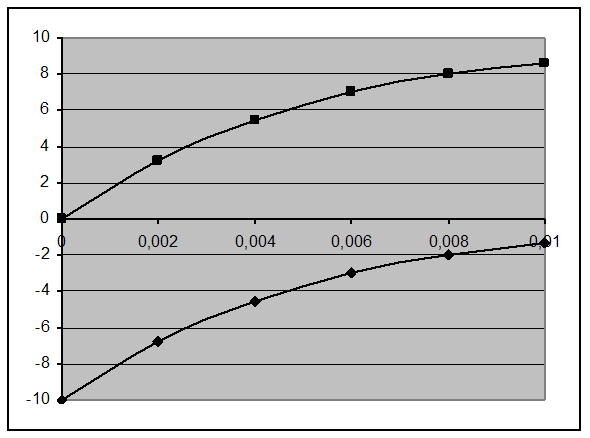
Мы получили кривую, называемую кривой заряда конденсатора. Так как период колебаний Т=0,02с, то конденсатор заряжается в течение времени t=0,01с, значит, для построения графика возьмем значения t, меньшие 0,01с  (на графике значения взяты с периодом через 0,002с).

Эта кривая, полученная расчетным путем, практически совпадает с кривой, снятой на осциллограмме.

По этому графику определим емкость конденсатора.

Воспользуемся методом касательных.

Если провести касательную, то можно определить постоянную времени t:

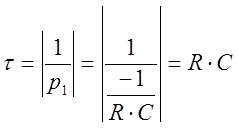
Значит: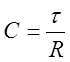

Из анализа графика следует, что t=0,002 c.

Так как метод касательных не является точным методом, то для более точного определения t решение u_c(t) запишем для момента времени t:

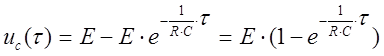
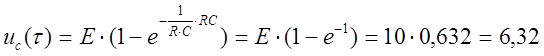 (B).

Отложим эту прямую на оси ординат.

Из графика видно, что этому значению u_c соответствует t≈0,0017=0,002(с), что почти  совпадает со значением t, найденным по методу касательных. Значит, ёмкость исследуемого конденсатора будет равна:

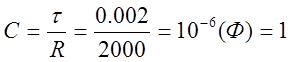 (мкФ).

   2. Разряд предварительно заряженного конденсатора на активном сопротивлении и индуктивности.

 

Рис 6

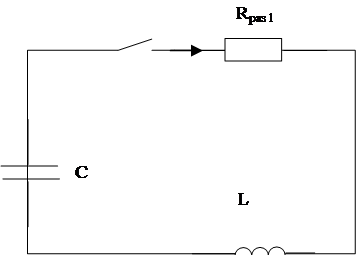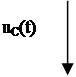Расчет будем производить классическим методом.

2.1 Определим ток через индуктивность и напряжение на емкости до коммутации.

u_c(0-)=u₀

i_L(0-)=0

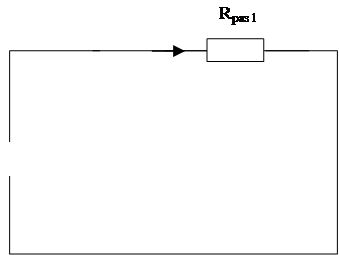
2.2  Найдем принужденные составляющие тока через индуктивность и напряжения на конденсаторе.

 

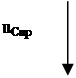Рис 7.

 i_{L пр} = 0 (ток через разрыв не течет)

u_{C пр} = 0

          2.3 Рассчитаем свободные составляющие:

 u_{c св} = u_c (0+) – u_{c пр}

Так как по второму закону коммутации u_c (0+) = u_c (0-)   ,то:

u_{c св} = u_c (0-) – u_{c пр} = u₀

i_{L св}(0)=i_L(0+) - i_{L пр}

Так как по первому закону коммутации i_L (0+) = i_L (0-)   ,то:

i_{L св}(0)=i_L(0-) - i_{L пр}=0

2.4  Составим характеристическое уравнение.

Закоротим в схеме источник ЭДС, разорвем цепь в любом месте и определим входное сопротивление, относительно этих зажимов:

 

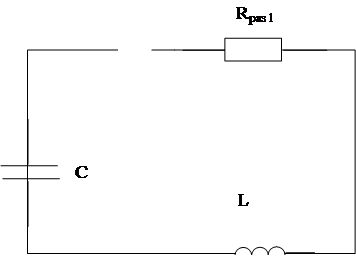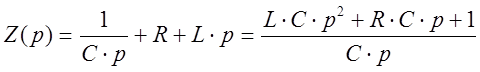                (2)

Здесь мы учли, что  .

, 

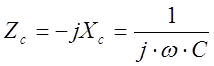Приравняв к 0 равенство (2), получим характеристическое уравнение:

Решим его: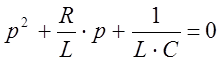

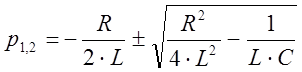
Вычислим подкоренное выражение:

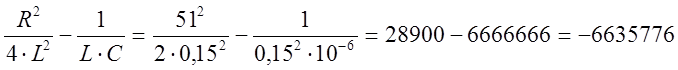
Д < 0, то есть процесс разряда конденсатора является колебательным, тогда корни характеристического уравнения вычисляются следующим образом:

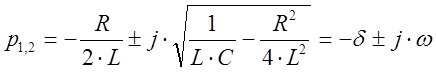
где d  - декремент затухания, равный: d= 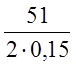= 170

w₀ – собственная частота колебаний контура, равная:

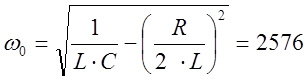
Значит, получилось 2 комплексно-сопряженных корня:

 

Решение для свободной составляющей записывается в виде:

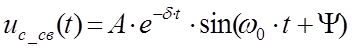
Решим задачу разряда конденсатора для этого случая.

Найдем производную:

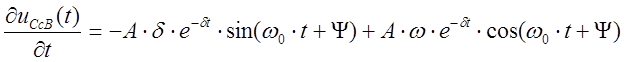
Для момента времени t=0:

∙sin y

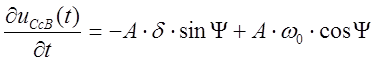
Так как    (пункт 2.3), то (приравнивая производную к 0) получим:

А∙sin y=u₀

Решим последнее уравнение:

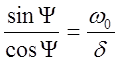
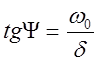
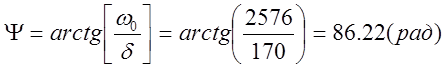
Для нахождения коэффициента  А решим следующее уравнение:

А∙sin y=u₀

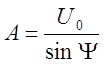
U₀ – максимальное напряжение, до которого зарядился конденсатор, в нашем случае оно равно 8,6 В.

Чтобы найти синус, воспользуемся свойствами прямоугольного треугольника.

			w0

 

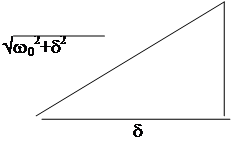Рис 9.

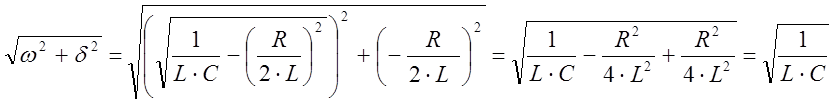
Из рис.9  видно, что:

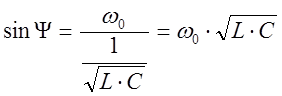
Значит:

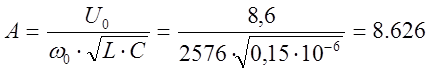
Общее решение найдем как сумму принуждающей и свободной составляющих, то есть:

Построим график этой функции.

При его построении строим сначала базовую синусоиду (учитывая, что угол задан в радианах):

          Y=8.626∙sin (2576t+86.2).

      Затем строим 2 симметричные экспоненты:

После этого графически складываем 2 решения.

График разряда конденсатора.

Мы получили график разряда конденсатора на разрядном сопротивлении и индуктивности. Из сравнения со снятой осциллограммой видно, что она совпадает с графиками полученными теоретическим путем. При совмещении двух графиков  получится кривая заряда-разряда конденсатора (осциллограмма) в течение одного периода колебаний поляризованного реле, то есть за время, равное t=0,01с, происходит заряд конденсатора и за такое же время происходит его разряд. Затем процесс повторяется.

Вывод: была освоена работа с осциллографом, рассчитаны переходные процессы, построены графики заряда конденсатора от источника ЭДС через зарядное сопротивление и его разряд через разрядное сопротивление и индуктивность.