Для розв’язання поставленої задачі побудуємо межу в комплексній площині параметра k.
![]() –
характеристичне рівняння.
–
характеристичне рівняння.
Зведемо характеристичне рівняння до вигляду , коли коефіцієнт а0 дорівнює одиниці: D(p)= pn + a1pn-1+ a2 pn-2+…+ an-1 p+an=0;
Відповідно отримаємо характеристичне рівняння:
![]()
Знаходимо параметр k:
![]()
Знаходимо комплексний вираз параметра k, використовуючи підстановку ![]()
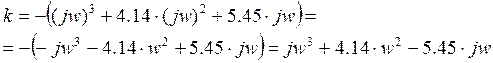
Виділимо дійсну А(w) і уявну В(w) складові:
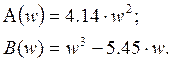
Задаючи значення ![]() від
від ![]() ,
побудуємо криву D-розбиття
Практично для цього слід знайти критичні точки, які відповідають переходам
кривої D - розбиття через дійсну і
уявну осі комплексної площини.
,
побудуємо криву D-розбиття
Практично для цього слід знайти критичні точки, які відповідають переходам
кривої D - розбиття через дійсну і
уявну осі комплексної площини.
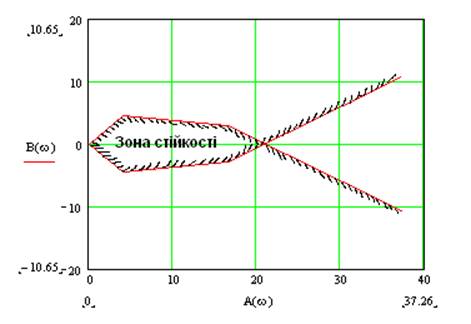
Рис.4.1 Крива d-розбиття
Із виразу ![]() можна
знайти значення
можна
знайти значення ![]() при якому
при якому ![]() рівне нулю, що відповідає переходу кривої D-розбиття через горизонтальну вісь.
Відповідні значення
рівне нулю, що відповідає переходу кривої D-розбиття через горизонтальну вісь.
Відповідні значення ![]() знайдемо із виразу:
знайдемо із виразу:
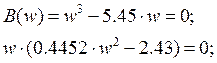
Звідки: ![]()
![]()
Виконані розрахунки
дають змогу встановити критичні значення параметра kкр=22,67 з врахуванням деякого запасу стійкості можна виділити зону
рекомендованих значень коефіцієнта підсилення розімкнутої системи. Визначена за правилом штриховки зона стійкості знаходиться зліва від кривої D-розбиття. Значення k вибирається по точках, які лежать на дійсній осі ![]() , тому що всі інші точки відповідають комплексним величинам,
а коефіцієнт k є реальною фізичною величиною.
, тому що всі інші точки відповідають комплексним величинам,
а коефіцієнт k є реальною фізичною величиною.
Отже, для забезпечення стійкості системи рекомендоване значення параметра k=1…20.
4.2.2 Дослідження системи на стійкість за допомогою критерію Михайлова
Оцінка стійкості системи за даними критеріями виконується на основі характеристики (годографа) Михайлова, яка будується таким чином.
1.
В характеристичному рівнянні замкнутої системи ![]() виконують підстановку
виконують підстановку ![]() , де
, де ![]() , після
чого вираз годографа Михайлова має вигляд:
, після
чого вираз годографа Михайлова має вигляд:
![]()
![]()
2. Для знаходження дійсної і уявної частин та побудови годографа Михайлова, дійсної і уявної складових застосуємо Mathcad.
Критерії Михайлова
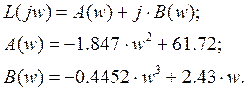
У комплексній площині будуємо годограф Михайлова (рис 4.2):
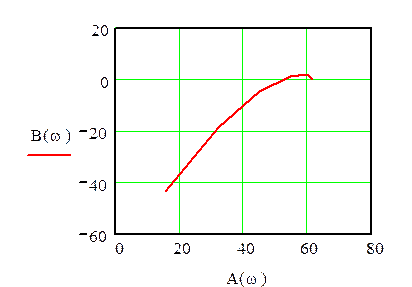
Рис.4.2 Годограф Михайлова
Радіус-вектор годографа Михайлова відповідає нестійкій системі, оскільки не витримується принцип послідовності обходу усіх квадратів комплексної площини.
Висновок
Результатом виконання курсового проекту є теоретичне обґрунтування можливості функціонування системи автоматизованого регулювання, функціональна схема якої наведена була вище.
Даний курсовий проект складається з чотирьох розділів. В процесі його виконання ми проводили аналіз ланок системи та системи в цілому. Була здійснена побудова (в другому розділі) амплітудно-частотних та фазочастотних характеристик ланок системи, розімкнутої системи та системи за збуренням. Також була виконана побудова лорарифмічних характеристик (в третьому розділі).
В четвертому розділі ми проводили дослідження системи на стійкість за алгебраїчними (критерії Гурвіца) та частотними (метод D-розбиття, критерії Михайлова) критеріями. В результаті дослідження система є нестійкою, за усіма показниками.
Отже, в процесі виконання курсового проекту ми отримали теоретичні знання з ТАУ та практичні навики з дослідження системи автоматичного регулювання.
Список використаної літератури
1. Теорія автоматичного управління / Під ред. А.А.Воронова. - М. : Вища школа. -1977.-Ч.I.-304с.
2. Попович М. Г., Ковальчук О. В. Теорія автоматичного керування: Підручник. – К.: Либідь, 1997. – 544 с.
3. Егоров К. В. Основи теорії автоматичного управління. – М.: “Енергія”, 1967.
4. Теорія автоматичного управління / Під ред. А.А.Воронова. – М.: Вища школа. –1977. –Ч. I. –304с.
5. Бесекерский В.А., Попов Е.П. Теорія автоматичного регулювання. - М. : Наука, 1974.
Додатки
Додаток А
Розрахункова таблиця амплітудно-частотних характеристик:
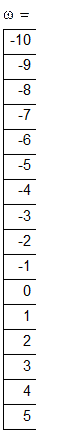

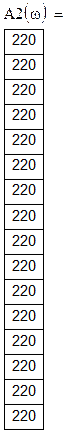

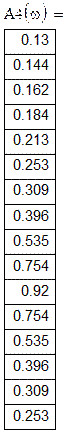


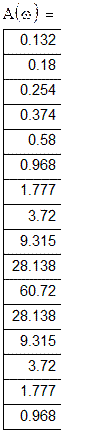
Розрахункова таблиця фазово-частотних характеристик:
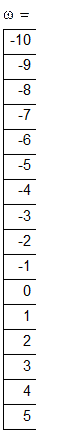
![]()
![]()
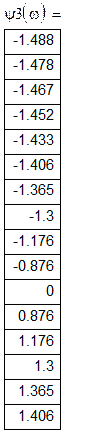
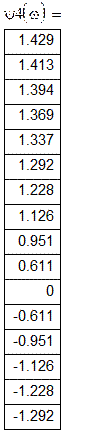
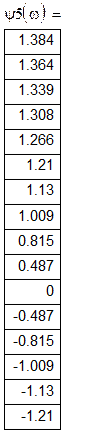
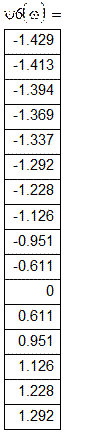
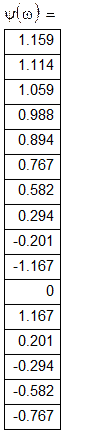
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.