Аналіз системи автоматичного керування. Аналіз ланок системи і системи в цілому. Структурна схема системи автоматичного керування, страница 3

Рис. 2.8 Амплітудно-фазові характеристики розімкнутої системи: а) характеристика в комплексній площині; б) амплітудно-частотна характеристика; в) фазочастотна характеристика.

РОЗДІЛ 3 ПОБУДОВА ЛОГАРИФМІЧНИХ ЧАСТОТНИХ ХАРАКТЕРИСТИК СИСТЕМИ

3.1 Побудова логарифмічних частотних характеристик ланок системи

При побудові логарифмічних характеристик по вертикальній осі відкладають логарифм відповідної величини в децибелах.

Амплітудно-частотна характеристика в децибелах матиме вигляд:

.

Фазочастотні логарифмічні характеристики будуються як  залежність:

.

При цьому на вертикальній осі відкладають фазу в радіанах  або в градусах, а по горизонтальній — w  в логарифмічному масштабі.

Ланка 1 - W₁(p)=k₁=0.25

Амплітудно-частотна характеристика:

Логарифмічна амплітудно-частотна характеристика:

 

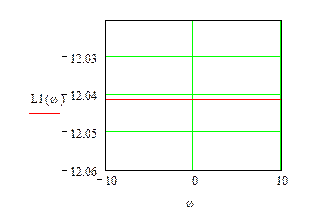
Рис.3.1 Логарифмічна амплітудно-частотна характеристика першої ланки

Ланка 2 – W₂(p)=k₂=220.  

Амплітудно-частотна характеристика:

Логарифмічна амплітудно-частотна характеристика:

.

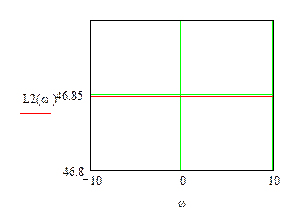
Рис.3.2 Логарифмічна амплітудно-частотна характеристика другої ланки

Логарифмічна амплітудно-частотна характеристика аперіодичних ланок першого порядку:

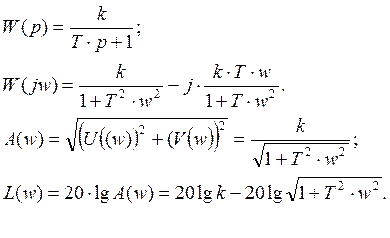
Ланка 3 - .

Амплітудно-частотна характеристика записується у вигляді:

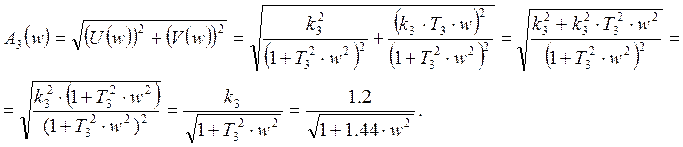
Логарифмічна амплітудно-частотна характеристика:

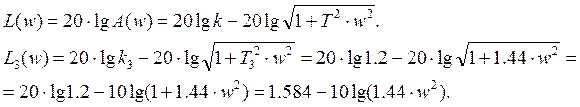
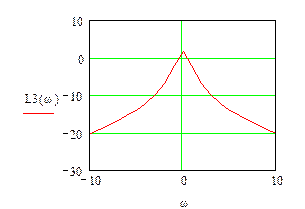
Рис.3.3 Логарифмічна амплітудно-частотна характеристика третьої ланки

Ланка 4 - .

Амплітудно-частотна характеристика записується у вигляді:

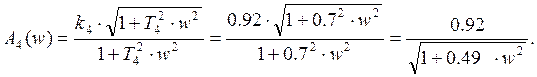
Логарифмічна амплітудно-частотна характеристика матиме вигляд:

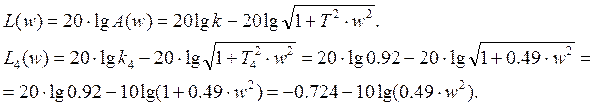
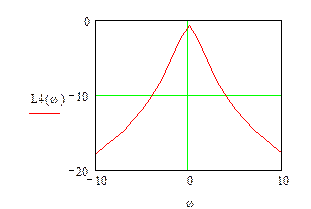
Рис.3.4 Логарифмічна амплітудно-частотна характеристика четвертої  ланки

Ланка 5 - .

Амплітудно-частотна характеристика записується у вигляді:

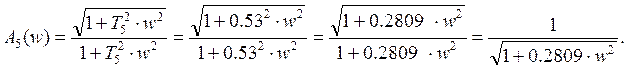
Логарифмічна амплітудно-частотна характеристика матиме вигляд:

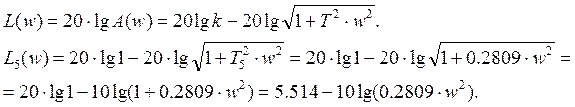
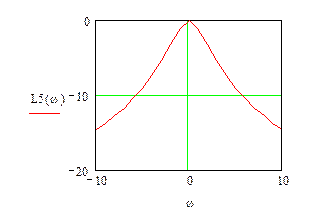
Рис.3.5 Логарифмічна амплітудно-частотна характеристика п’ятої ланки

Ланка 6 - .

Амплітудно-частотна характеристика записується у вигляді:

Логарифмічна амплітудно-частотна характеристика диференціюючої ланки.

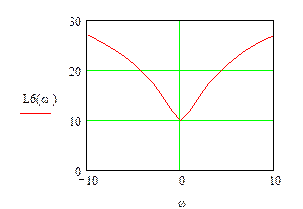
Рис.3.6 Логарифмічна амплітудно-частотна характеристика шостої ланки

3.2 Побудова логарифмічних частотних характеристик розімкнутої системи

При побудові результуючих частотних характеристик для групи послідовно з'єднаних ланок результуючий модуль (амплітудно-частотна характеристика розімкнутої системи) можна дістати як добуток модулів всіх ланок, а результуючу фазочастотну характеристику - як суму фазочастотних характеристик відповідних ланок. Тоді:

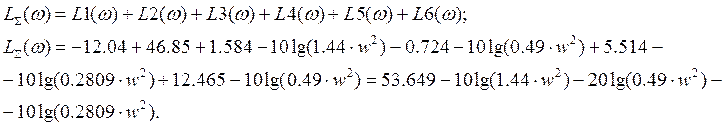
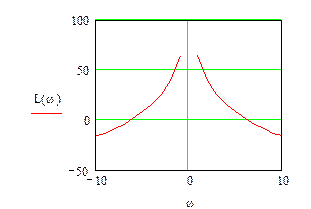
Рис.3.7 Логарифмічна амплітудно-частотна характеристика розімкнутої системи

3.3 Побудова логарифмічних частотних характеристик системи за збуренням

Амплітудно-частотна характеристика записується у вигляді:

=

=.

Логарифмічна амплітудно-частотна характеристика системи за збуренням системи:

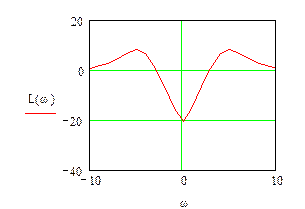
Рис.3.8 Логарифмічні амплітудно-частотні характеристики системи за збуренням

РОЗДІЛ 4 ДОСЛІДЖЕННЯ СИСТЕМИ НА СТІЙКІСТЬ

4.1 Дослідження системи на стійкість за алгебраїчними критеріями (критерій Гурвіца)

Дослідимо дану систему за критеріями Гурвіца. 

Прирівняємо знаменник передаточної функції замкнутої системи до нуля і запишемо характеристичне рівняння:

Знаходимо визначник Гурвіца користуючись такими правилами:

·  по головній діагоналі записуємо коефіцієнт характеристичного рівняння ;

·  місця зверху від діагоналі заповнюємо коефіцієнтами з більшим індексом, а знизу від діагоналі – з меншим індексом. При відсутності коефіцієнтів ставимо нулі.

·  діагональні мінори визначаємо із головного детермінанта Гурвіца викреслюванням відповідних стовпчиків і рядків.

Коефіцієнти дорівнюють

Визначаємо діагностичні мінори :

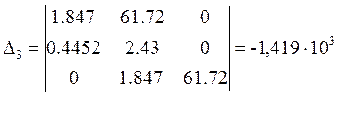
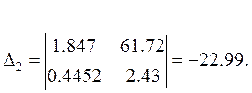
Система вважається стійкою у випадку якщо a₀>0, a₁>0, a₂>0, a₄>0, ∆₄>0, ∆₃>0, ∆₂>0. Отже, система є нестійкою, бо ∆₃<0, ∆₂<0.

4.2 Дослідження системи  на стійкість за частотними критеріями

4.2.1 Дослідження системи на стійкість методом d-розбиття