
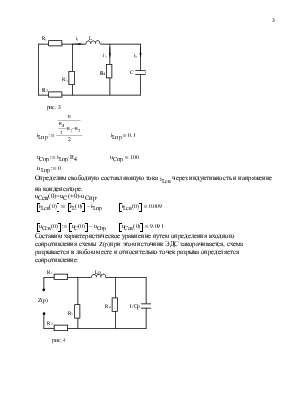









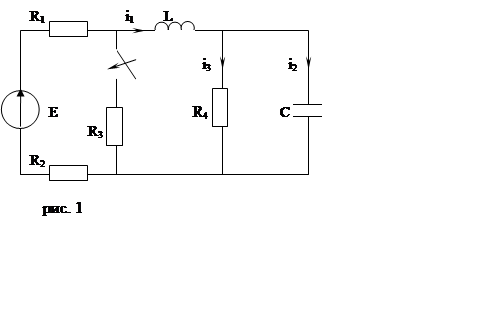
Задача 1. Дана электрическая цепь, в которой происходит
коммутация. В цепи действует постоянная ЭДС E. Требуется определить закон
изменения во времени одной из величин после коммутации. Задачу решить 2
методами - классическим и операторным. Построить график изменения искомой
величины во времени на интервале от t=0 до t=3/|p|min, где |p|min -
наименьший по модулю корень характеристического уравнения.
![]()
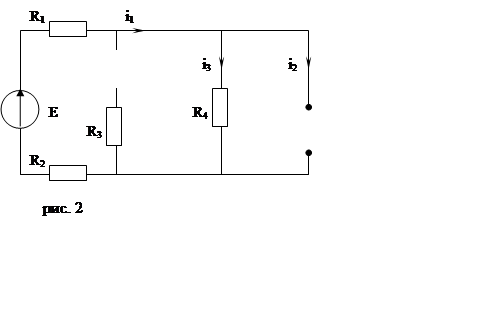
Находим ток через индуктивность до коммутации и
напряжение на емкостях:
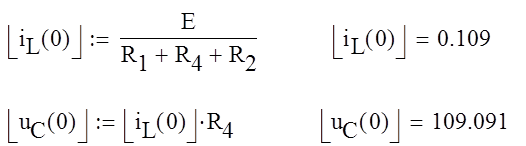
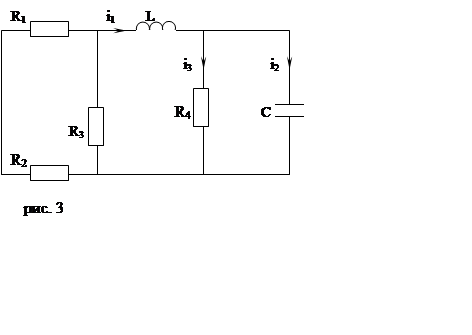
Применим 1 и 2 законы коммутации iL(+0)=iL(-0), uC(+0)=uC(-0).
Определим принужденную составляющую тока iL через индуктивность и напряжение на конденсаторе в цепи после коммутации:
 |
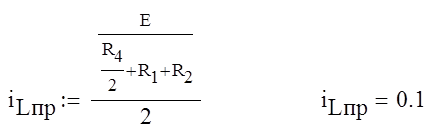

![]()
Определим свободную
составляющую тока ![]() через индуктивность и
напряжение на конденсаторе.
через индуктивность и
напряжение на конденсаторе.
uCсв(0)=uC(+0)-uCпр.
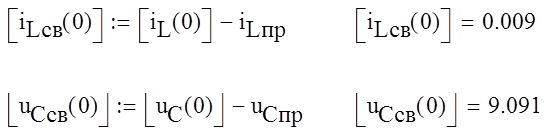
 |
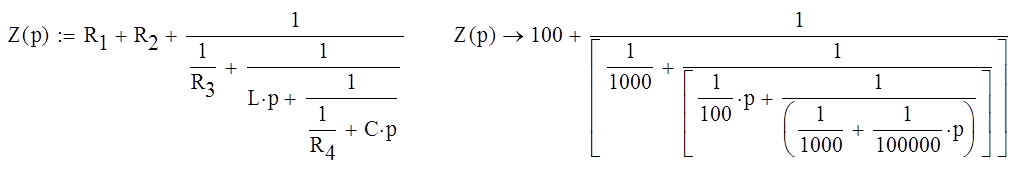
Составим и решим характеристическое уравнение:
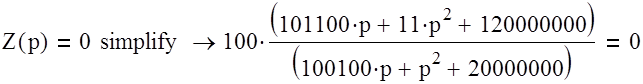
Решим получившееся квадратное уравнение
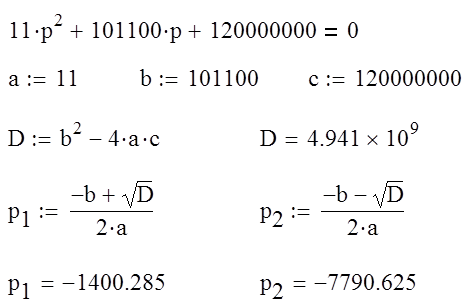
У нас получилось два отрицательных, неравных между собой, действительных корня, и свободная составляющая заапишется в виде следующего выражения:
iLсв = A1ep1t+A2ep2t
Для нахождения неизвестных коэффициентов A1,A2 составим систему уравнений включаюшая решение и производную до n-1 порядка включительно, так как у нас два корня нам нужно найти производную первого порядка:
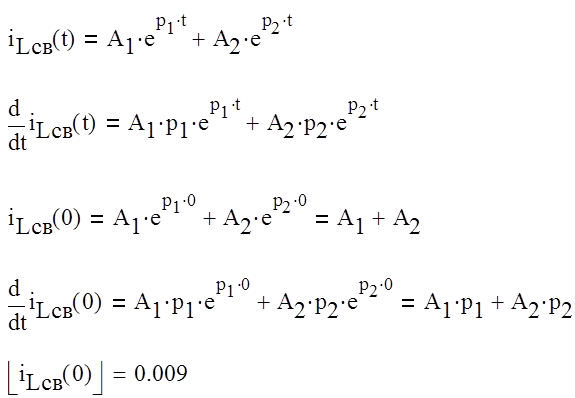
Найдем diLсв(+0)/dt:
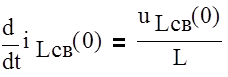
По 2 закону Кирхгофа найдем uLсв(+0):
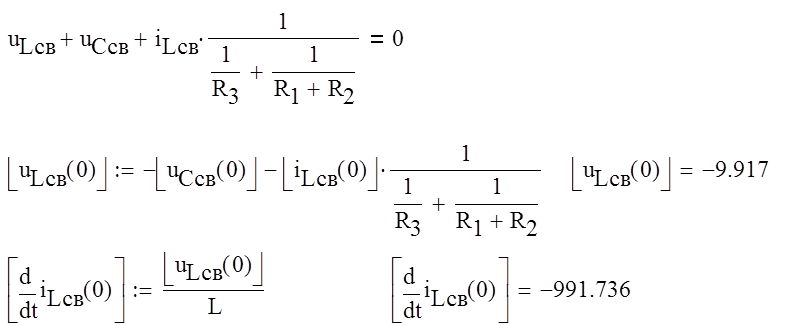
Решим систему относитльно неизвестных коэффициентов А
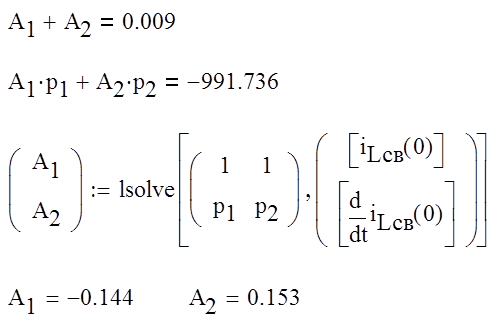
Запишем решение для искомого iL
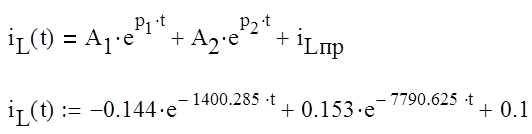
Найдем напряжение на индуктивности uL в общем виде :
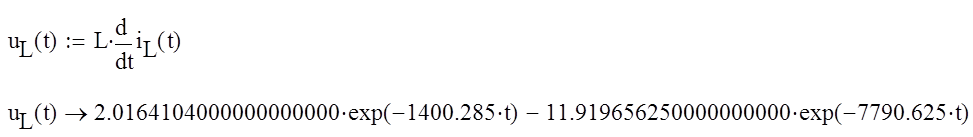
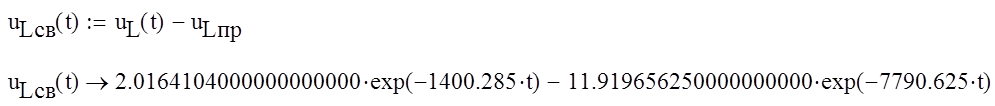
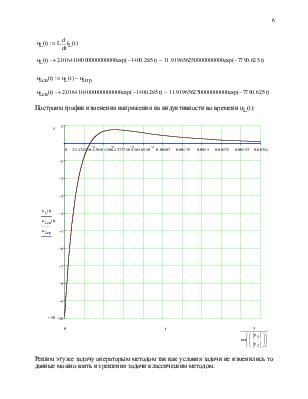
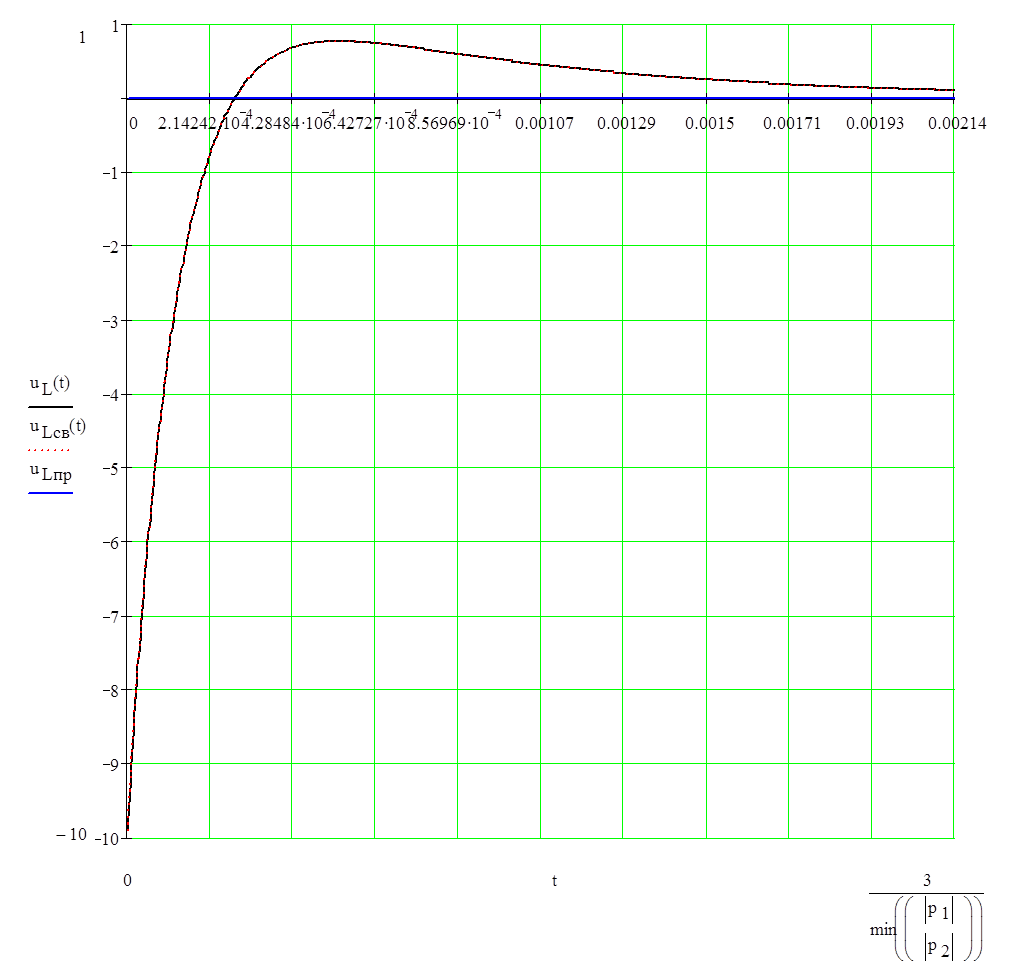
Построим график изменения напряжения на индуктивности во времени uL(t):
Решим эту же задачу операторым методом так как условия задачи не изменились то данные можно взять из решения задачи классическим методом.
Найдем напряжения на емкостях и ток через индуктивность в начальный момент времени uC(0) и iL(0):
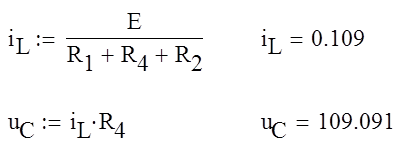
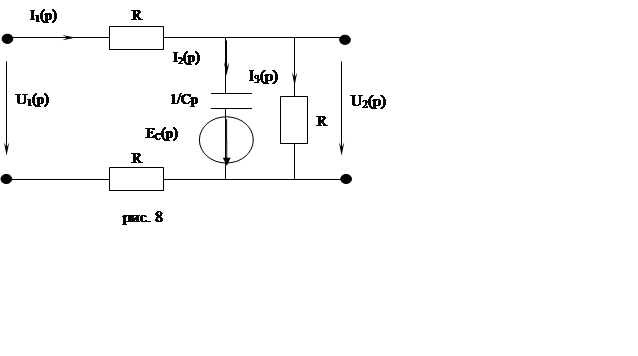
Составим операторную схему замещения для до коммутационной схемы.
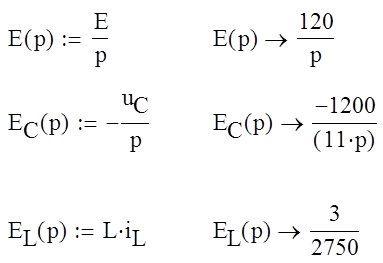
Составим систему уравнений по законам Кирхгофа и решим ее (матричны методом):
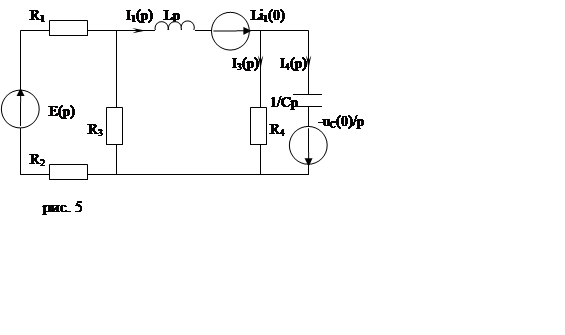 |
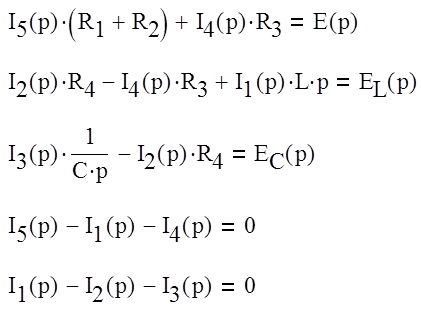
Нам необходимо расчитать только ток ![]()

Ток ![]() будет равен:
будет равен:
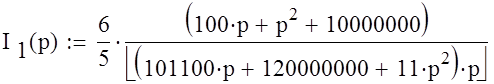
По закону Ома:
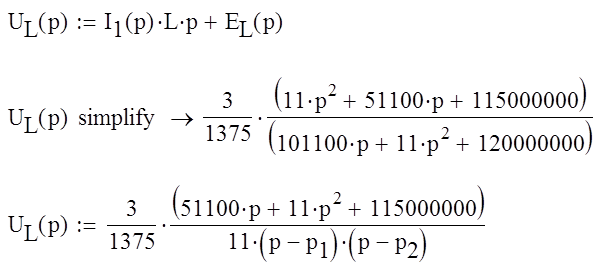
Используя обратное преобразование Лапласа, найдем оригинал напряжения uL(t):
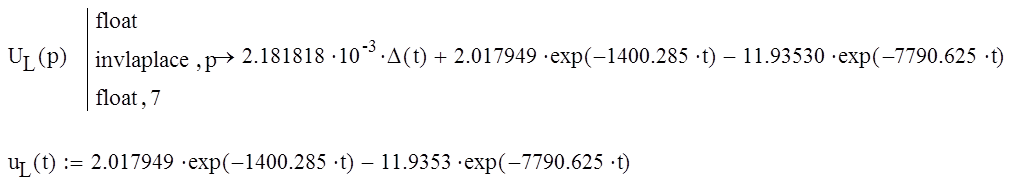
Результаты полученные классическими и операторными методами
совпадают но с небольшими отклонениями, эти ошибки вызваны в погрешнностях
вычислений и равны ![]() (бесконечно малая величина)
что позволяет считать вычисления верными.
(бесконечно малая величина)
что позволяет считать вычисления верными.
 |
Найдем переходную функцию тока g(t) операторным методом.
Найдем ток через индуктивность до коммутации и сразу после коммутации:
![]()
Пусть напряжение u1(t) изменилось скачком на 1 В:
![]()
Решение проведем операторным методом.
На вход нашей схемы подадим испытательную функцию Хевисайда.
 |
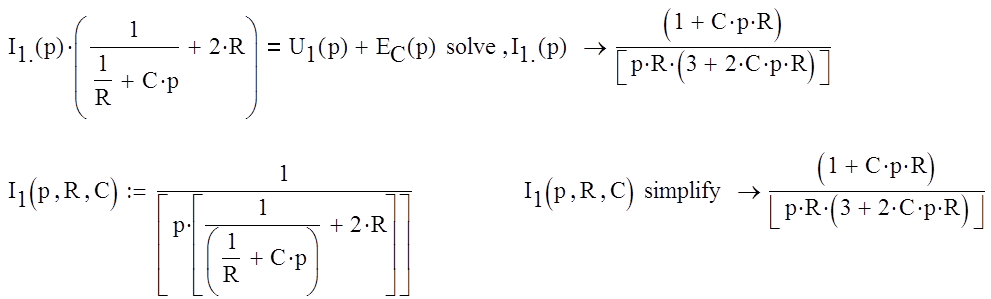
Найдем оригинал тока i1(t), используя обратное преобразование Лапласа:
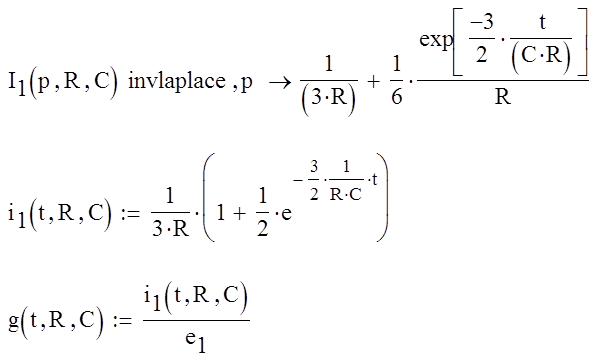
Запишем интеграл Дюамеля в 1 форме:
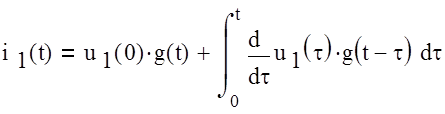
Решим интеграл на 2-х интервалах времени: от 0 до t1 и от t1 до ![]() .
.
Для первого интервала:
![]()
Подставим значение в интеграл и вычислим его
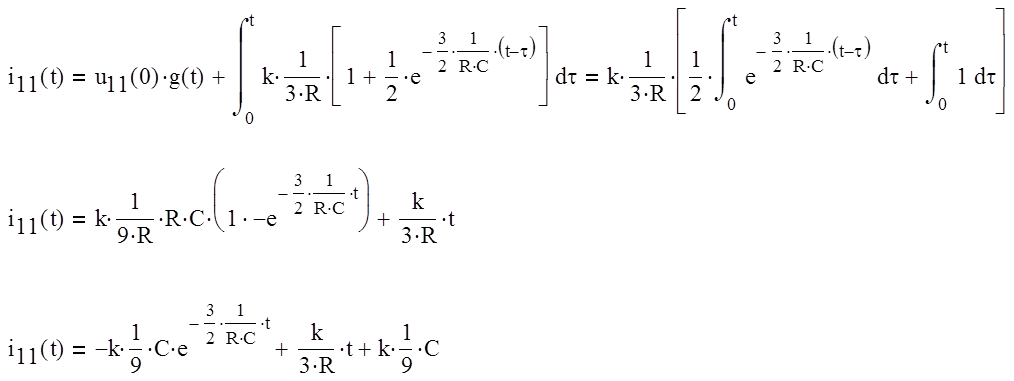
Для второго интервала:
![]()
Подставим значение во второй интеграл и вычислим его
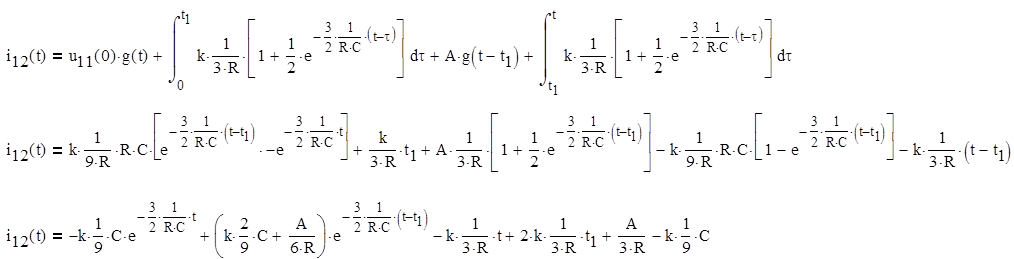
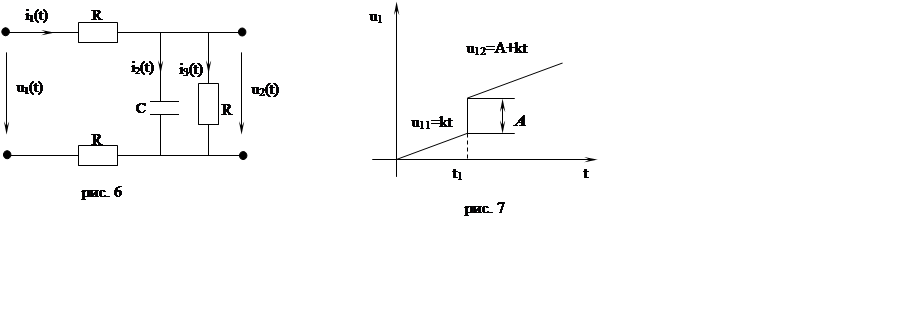
Задача 3. Дано качественное изображение импульса напряжения и его аналитическое выражение. Требуется:
1) Получить аналитическое выражение для модуля и аргумента спектра этой функции U(jw) = |U(jw)|ejy(w)
2) Полученное выражение |U(jw)| представить в функции безразмерной величины w/a
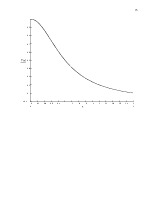
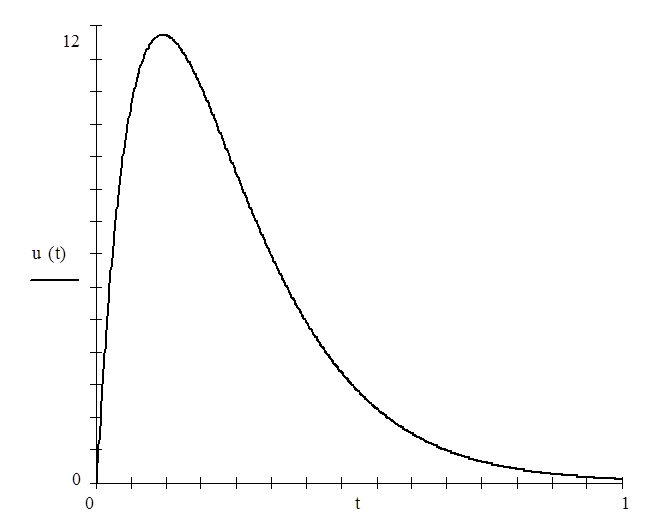
3) Построить зависимость |U(jw)| в функции w/a (если полученное выражение не содержит a, то построить зависимость в функции w). При построении графика ограничиться значениями w/a, при которых ордината кривой достигает 0,1-0,2 от ее максимального значения.
![]()
По условию нам задана следующая функция
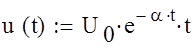
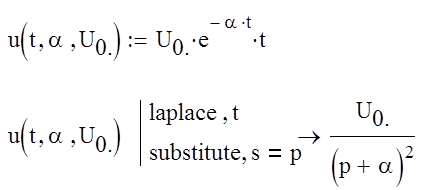
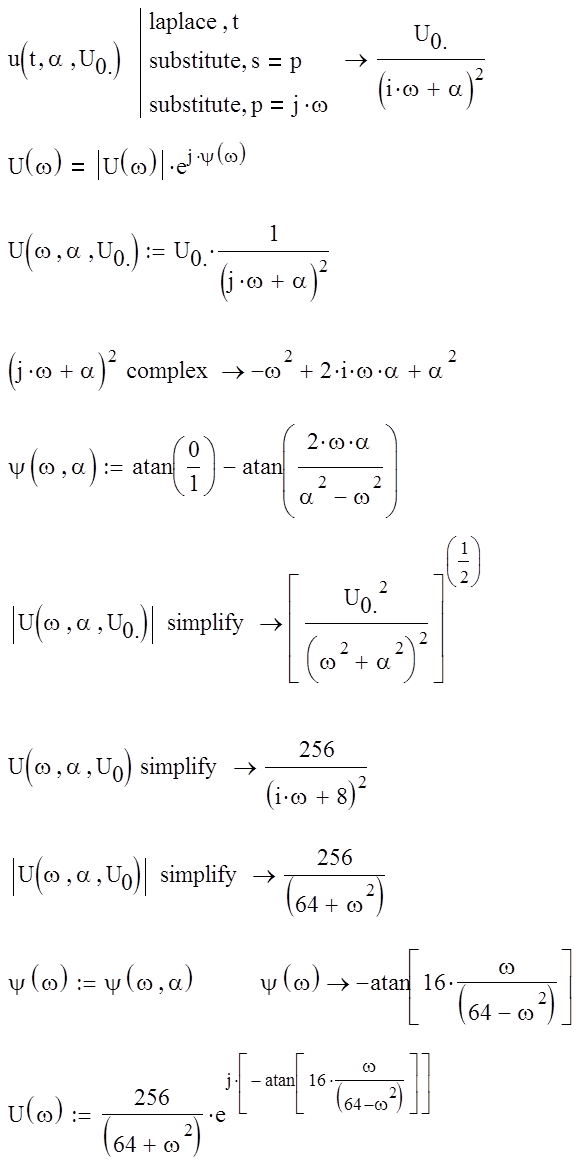
Разделим чилитель и знаменатель на α2
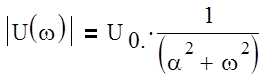
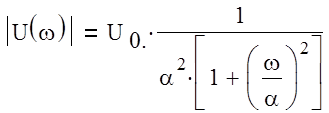
Для построения модуля фукции в относительных единицах проведем дополнительные преобразования.
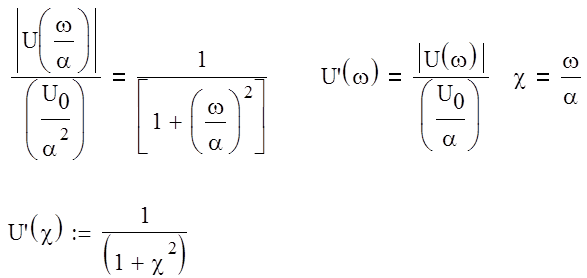
Построим график функции
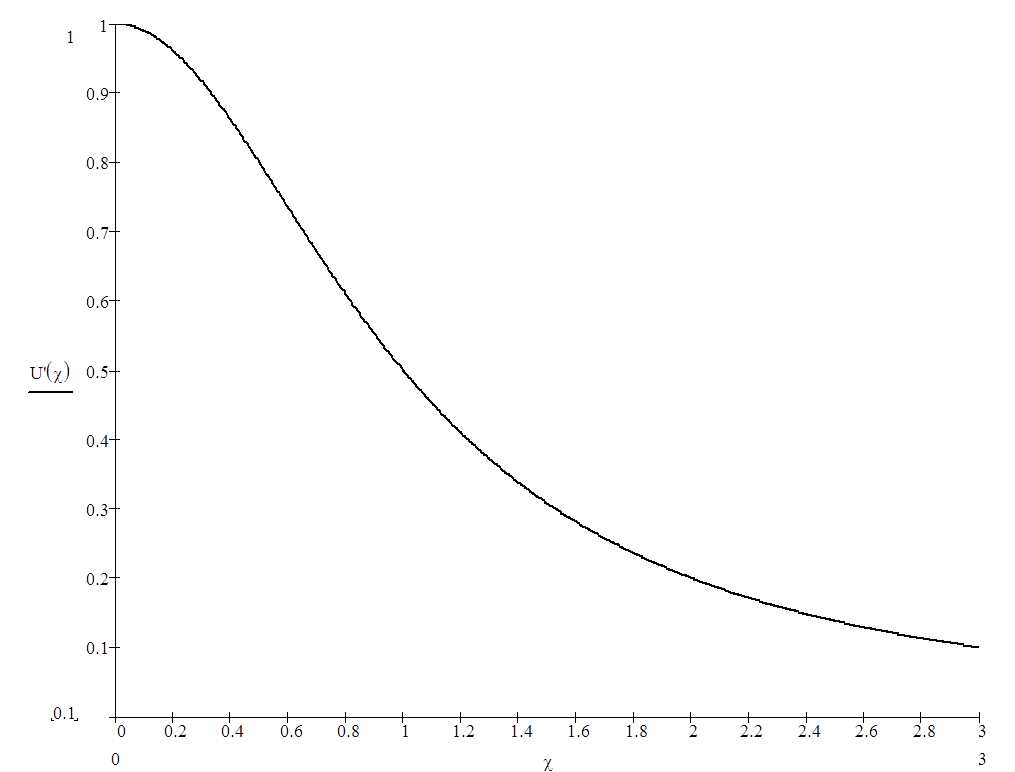
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.