Определение первичных параметров линии. Определение напряжения U1, тока I1, мощности в начале и конце линии, КПД линии

Исходные данные (16 вариант):

f = 10 кГц                       U₂ = 50 В

l = 1   км                          Z_н = 1400e^-j7º Ом

a = 50 мм                         Тип – ВЛ 

r = 0,4 мм

1. Определяем первичные параметры линии:

 - сопротивление проводов двухпроводной медной линии на постоянном токе:

   ρ – удельное сопротивление проводов при t=20º; для меди  ρ=0,01785 Ом*мм²/м;

 

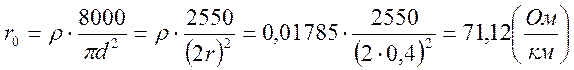
 - поправочный коэффициент F(x), учитывающий увеличение активного сопротив   ления за счёт поверхностного эффекта:

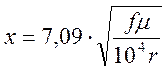      для меди  µ=1;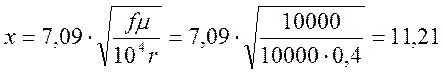           

По таблице определяем F(x):

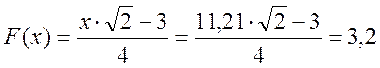  ;    тогда

R₀=r₀(1+F(x))=71,12(1+3,2)=298,7 (Ом/км)

Индуктивность двухпроводной линии

  ;    

   .

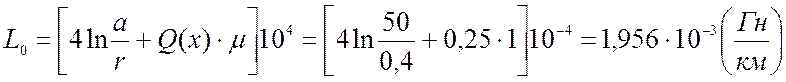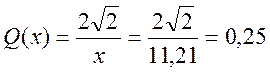Ёмкость двухпроводной воздушной линии на единицу длины:

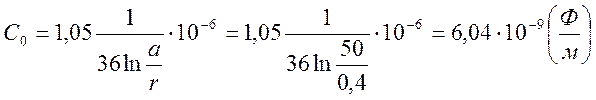
Проводимость единицы длины линии:

G₀=G’+nf=1×10^-8+5×10^-11×10⁴=5,1×10^-7 (См/км),    где

G’ – проводимость изоляции на постоянном токе, равная 1×10^-8 (См/км) при сухой                   погоде.

n – коэффициент диэлектрических потерь, равный  5×10^-11   (См/км×Гц) при сухой                   погоде.

2. Определяем напряжение U₁, ток I₁, мощности в начале и конце линии, КПД линии

а) Определяем вторичные параметры линии:

- полное комплексное сопротивление единицы длины линии:

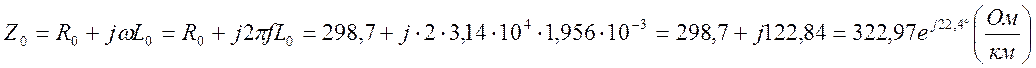- полная комплексная проводимость единицы длины линии:

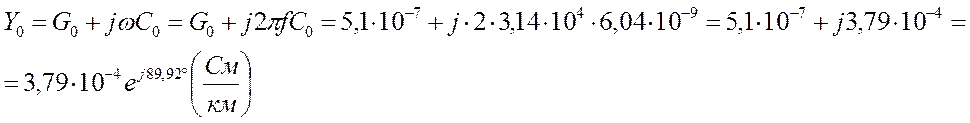
- волновое сопротивление линии:

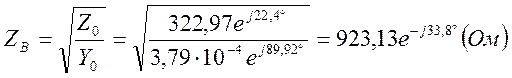
- комплексный коэффициент распространения:

γl = αl+jβl = (0,195+j0,29)×1 = 0,195+j0,29

затухание сигнала αl = 0,195 (Нп)

изменение фазы βl = 0,29 (рад)

б) Запишем уравнения для линии с потерями через параметры конца линии:

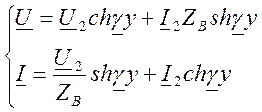
Для расчёта напряжения и тока в начале линии U₁и I₁ вместо y подставляем l, тогда:

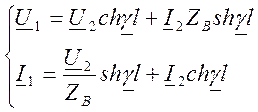
Так как ток I₂ в конце линии неизвестен, но известны нагрузка и напряжение в конце линии, то найдём его:

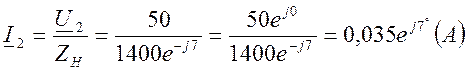
Рассчитываем и , для этого воспользуемся следующими соотношениями:

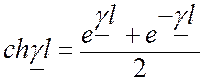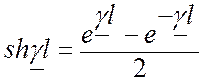               ;                   где

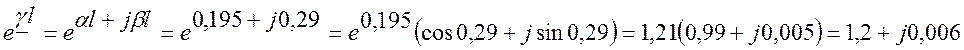
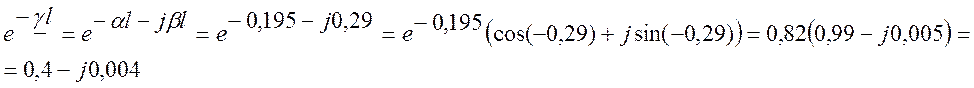
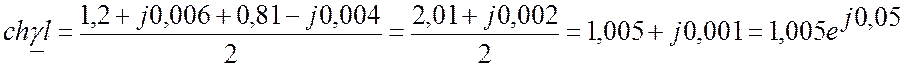
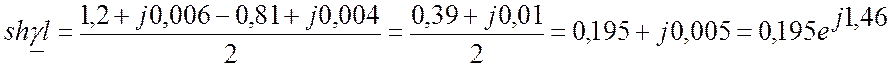
Рассчитаем U₁ и I₁ в начале линии:

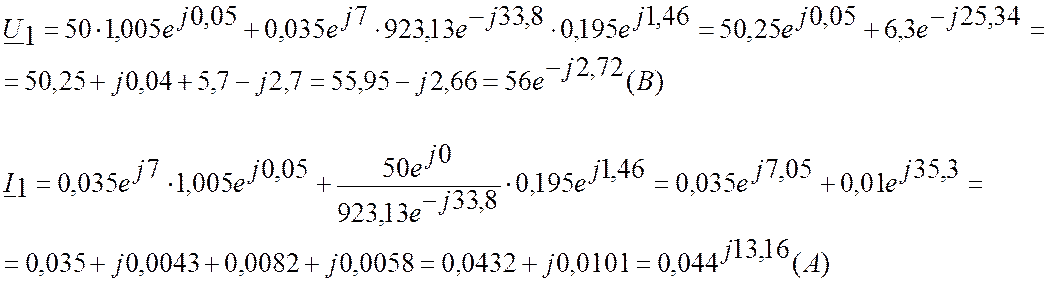
в) Рассчитаем полную комплексную мощность в начале и конце линии и КПД линии

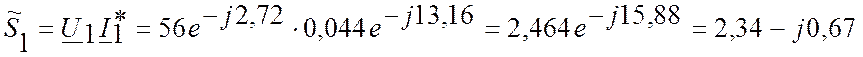
Полная мощность         S₁=2,464  (BA)

Активная мощность     P₁=2,34    (Вт)

Реактивная мощность  Q₁=-0,67  (вар)

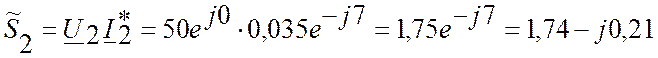
Полная мощность         S₂=1,75  (BA)

Активная мощность     P₂=1,74   (Вт)

Реактивная мощность  Q₂=-0,21 (вар)

Определяем КПД линии:

η=(Р₁/Р₂)×100%=(1,74/2,34)×100%=74,36%

3. Для линии без потерь определяем напряжение U₁ и ток I₁ в начале линии, а также длину электромагнитной волны λ:

а) Для линии без потерь R₀=0, G₀=0

Нагрузка стала активной

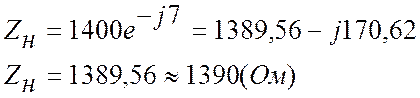
Коэффициент фазы

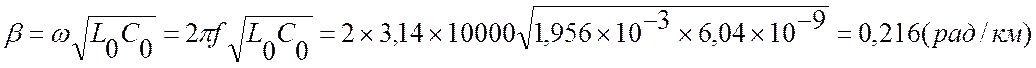
Определяем изменение фазы сигнала по всей длине линии

Определяем волновое сопротивление

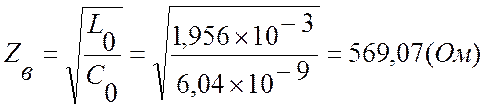
б) Напряжение и ток в начале линии без потерь

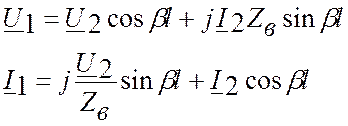
тогда

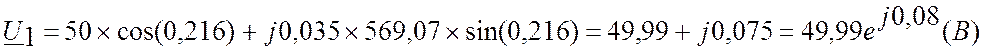
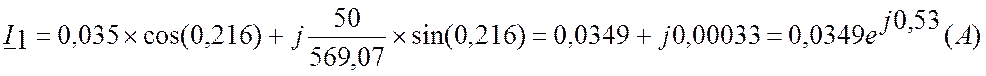
Длина электромагнитной волны λ:

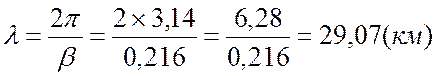
4. Построим график U=f(βy) для линии без потерь:

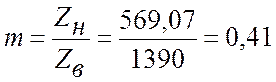
	0			2,16
	0	3,634	7,258	1
	1		0	0,976
	1	0,5	0	0,952
	0		1	0,214
	0		1	0,0458
	0	0,084	0,1681	0,0077
	50	38,21	20,5	48,98