Характеристика стали 12Х18Н9 (химический состав, механические и технологические свойства, область применения). Аппроксимация кривой деформирования степенной зависимостью, страница 2

Химический состав стали 12Х18Н9 представлен в таблице 4.

Таблица 4. Химический состав стали 12Х18Н9 [3]

Химический элемент	%
Кремний (Si), не более	0,8
Медь (Cu), не более	0,30
Марганец (Mn), не более	2,0
Никель (Ni)	8,0-10,0
Титан (Ti), не более	0,5
Фосфор (P), не более	0,035
Хром (Cr)	17,0-19,0
Сера (S), не более	0,020

Технологические свойства

Температура ковки: начала , конца . Сечения до 350 мм охлаждаются на воздухе. Свариваемость: без ограничений.

Механические свойства стали при нормальных условиях и при повышенных температурах представлены в таблицах 5 и 6.

Таблица 5. Механические свойства стали 12Х18Н9 [3]

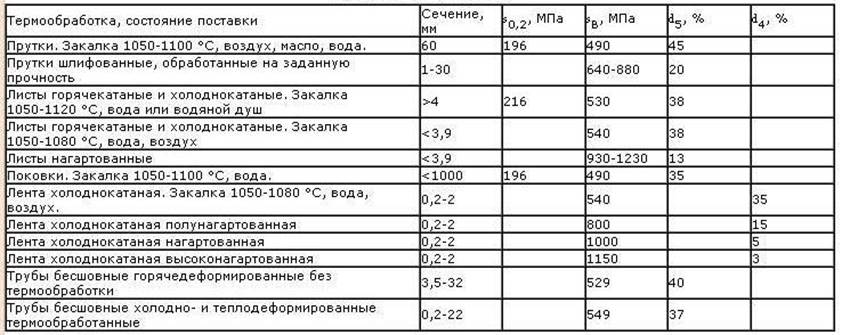
Таблица 6. Механические свойства при повышенных температурах[3]

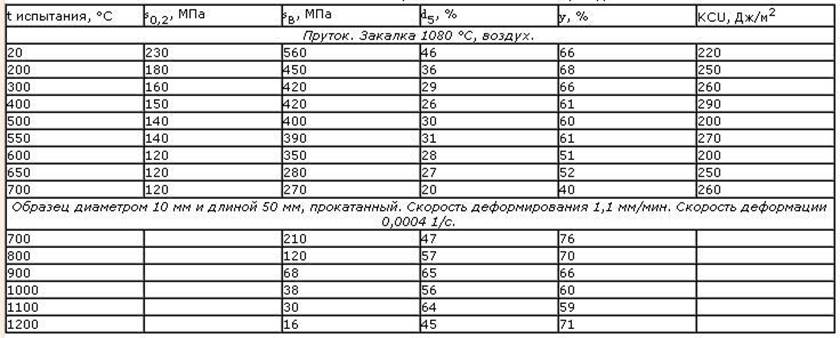
3  АППРОКСИМАЦИЯ КРИВОЙ ДЕФОРМИРОВАНИЯ  СТЕПЕННОЙ  ЗАВИСИМОСТЬЮ

3.1 Аппроксимация диаграммы деформирования при линейном напряженном состоянии

Все расчетные формулы заимствованы из учебного пособия [1].

При сопоставлении различных способов аппроксимации диаграмм деформирования пластичных конструкционных материалов, на которых отсутствует площадка текучести, с экспериментальными данными было установлено, что определенными преимуществами (простота, адекватность) обладает функция вида

(1)

(аппроксимация диаграммы деформирования по Рамбергу-Осгуду), где  – истинное напряжение;

K, m – постоянные материала, зависящие от температуры и скорости деформирования;

 – логарифмическая пластическая деформация; при  можно считать  (максимальное отличие не превышает 0,5%).

Поскольку диаграммы истинных и условных напряжений в области предела текучести практически совпадают: , , при известном значении показателя упрочнения m коэффициент прочности K может быть найден исходя из равенства

                                           (2)

С другой стороны, известно, что диаграмма условных напряжений пластичного материала имеет отчетливо выраженный максимум, то есть, при  в точке, соответствующей временному сопротивлению, производная . Учитывая связь истинного и условного напряжения(), последнее можно представить в функции логарифмической неупругой деформации:

Дифференцируя это выражение по параметру p и приравнивая получившийся результат нулю,

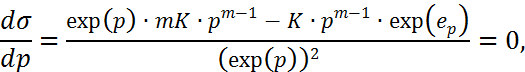
получаем

Соответственно определим коэффициент прочности K:

                                                 (3)

И, наконец, величина Kможет быть найдена путем осреднения этих двух результатов:

                             (4)

Обычно все три значения K не слишком отличаются друг от друга, тем не менее, если предполагается работать в области сравнительно не больших пластических деформаций, целесообразно использовать формулу (2), высоких,  в частности,  в области разрушения – (3). Будем в расчетах использовать осредненное значение K (4).

Опыт расчетов показывает, что для конструкционных сталей и сплавов величина показателя упрочнения m изменяется в пределах . Оказалось, что внутри данного диапазона зависимость  допустимо аппрксимировать линейной функцией. В результате обработки представительного набора опытных данных и определения методом наименьших квадратичных отклонений констант названной зависимости были получены удобные для практических расчетов выражения:

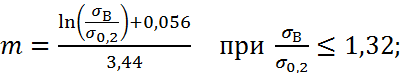                          (5)

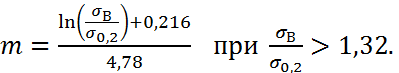                      (6)

Найдем значение показателя упрочнения m, а затем и коэффициента прочности K, подставляя в формулы исходные данные:

таким образом m будем находить по формуле (6):

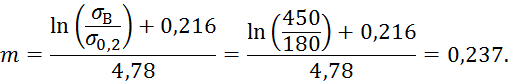
Зная показатель упрочнения m найдем коэффициент прочности K:

Из вышеизложенного следует, что действительные значения  временного сопротивления  и напряжения в момент разрушения  (истинное сопротивление разрыву) определяются следующими зависимостями: