Первая отличная от нуля производная функции в точке a =
0 - пятая, поэтому эта точка - нуль пятого порядка функции ![]() .
Теорема. Для того, чтобы
аналитическая в точке а функция f(z) имела
в этой точке нуль k -го порядка, необходимо и достаточно,
чтобы в окрестности этой точки функция f(z)представлялась
в виде f( z) = (z − a) k·φ(z),
где φ(z) - аналитическая в точке а функция,
и φ(a) ≠ 0.
Доказательство. Необходимость. Пусть
точка а - нуль k-го порядка
функции f(z), т.е. f(a)
= f ′(a) = f ″(a)
= ... = f (k−1)(a)
= 0, и f (k)(a)
≠ 0. Тогда её разложение в ряд Тейлора имеет вид
.
Теорема. Для того, чтобы
аналитическая в точке а функция f(z) имела
в этой точке нуль k -го порядка, необходимо и достаточно,
чтобы в окрестности этой точки функция f(z)представлялась
в виде f( z) = (z − a) k·φ(z),
где φ(z) - аналитическая в точке а функция,
и φ(a) ≠ 0.
Доказательство. Необходимость. Пусть
точка а - нуль k-го порядка
функции f(z), т.е. f(a)
= f ′(a) = f ″(a)
= ... = f (k−1)(a)
= 0, и f (k)(a)
≠ 0. Тогда её разложение в ряд Тейлора имеет вид 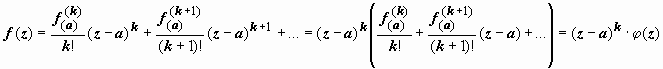 , где
, где 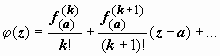 -
аналитическая (как сумма степенного ряда с тем же кругом сходимости, что и у
ряда для f(z)) функция,
-
аналитическая (как сумма степенного ряда с тем же кругом сходимости, что и у
ряда для f(z)) функция, 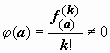 .
Достаточность. Пусть f( z)
= (z − a) k·φ(z),
где φ(z) - аналитическая в точке а функция,
и φ(a) ≠ 0. Находим производные этой функции по
формуле Лейбница( uv ) (n) = u (n) v + n u (n -
1) v ′ + Cn2 u (n -
2 ) v ″ + Cn3 u (n -
3 ) v(3 ) + … + Cn2 u ″ v (n -
2) + n u ′ v (n -
1 ) + u v (n ): f ′(z)
= k(z − a)k -
1 φ(z) + (z − a)k φ ′(z), f ′(a)
= 0; f ″(z) = k (k −
1)(z − a)(k - 2) φ(z)
+ 2k (z − a)(k -
1) φ′(z) + (z − a)(k) φ″(z), f ″(a)=0;
f ( k -1 )(z)
= k·( k -1 )·…2·(z − a) φ(z)
+ C1k-1k·( k -1
)·…3·(z − a)2 φ ′(z)
+ … + (z − a) k φ(k -1)(z), f ( k -1)(a)=0;
f ( k)(z)
= k·( k -1 )·…2·1·φ(z) + C1k k·( k -1
)·…2·(z − a) φ ′(z)
+ … + (z − a) k φ(k)(z), f ( k)(a)
= k!·φ(a) ≠ 0, что и требовалось
доказать.
Из этой теоремы следует, что
если многочлен P n(z) = a0 z n + a1 z n -
1 + a2 z n -
2 + … + a n - 1 z =
0 разложен на множители P n(z)
= a0 (z − z1) k1 (z − z2) k2 …
(z − zl) kl ,
то корни z1, z2,
…, zlявляются нулями функции P n(z) кратностей,
соответственно, k1, k2,
…, kl.
.
Достаточность. Пусть f( z)
= (z − a) k·φ(z),
где φ(z) - аналитическая в точке а функция,
и φ(a) ≠ 0. Находим производные этой функции по
формуле Лейбница( uv ) (n) = u (n) v + n u (n -
1) v ′ + Cn2 u (n -
2 ) v ″ + Cn3 u (n -
3 ) v(3 ) + … + Cn2 u ″ v (n -
2) + n u ′ v (n -
1 ) + u v (n ): f ′(z)
= k(z − a)k -
1 φ(z) + (z − a)k φ ′(z), f ′(a)
= 0; f ″(z) = k (k −
1)(z − a)(k - 2) φ(z)
+ 2k (z − a)(k -
1) φ′(z) + (z − a)(k) φ″(z), f ″(a)=0;
f ( k -1 )(z)
= k·( k -1 )·…2·(z − a) φ(z)
+ C1k-1k·( k -1
)·…3·(z − a)2 φ ′(z)
+ … + (z − a) k φ(k -1)(z), f ( k -1)(a)=0;
f ( k)(z)
= k·( k -1 )·…2·1·φ(z) + C1k k·( k -1
)·…2·(z − a) φ ′(z)
+ … + (z − a) k φ(k)(z), f ( k)(a)
= k!·φ(a) ≠ 0, что и требовалось
доказать.
Из этой теоремы следует, что
если многочлен P n(z) = a0 z n + a1 z n -
1 + a2 z n -
2 + … + a n - 1 z =
0 разложен на множители P n(z)
= a0 (z − z1) k1 (z − z2) k2 …
(z − zl) kl ,
то корни z1, z2,
…, zlявляются нулями функции P n(z) кратностей,
соответственно, k1, k2,
…, kl.
1.2.
Изолированные особые точки.
1.2.1. Определение. Точка а называется изолированной
особой точкой функции f(z), если
существует окрестность этой точки, в которой f(z) аналитична
во всех точках, за исключением точки а.
Рассмотрим разложение
функции f(z) в ряд Лорана 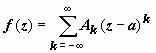 в окрестности
изолированной особой точки а. При этом возможны следующие
случаи.
1. Главная часть ряда
Лорана отсутствует:
в окрестности
изолированной особой точки а. При этом возможны следующие
случаи.
1. Главная часть ряда
Лорана отсутствует: 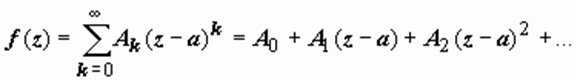 .
В этом случае особая
точка а называется устранимой.
2. Главная часть
содержит конечное число членов:
.
В этом случае особая
точка а называется устранимой.
2. Главная часть
содержит конечное число членов: 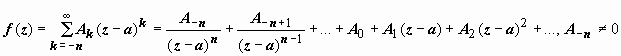 .
В этом случае особая точка а
называется полюсом n-го порядка. Если n =1,
полюс называется простым, в остальных случаях - кратным.
3. Главная часть
содержит бесконечно много членов. В этом случае особая точка а называется
существенно особой точкой.
.
В этом случае особая точка а
называется полюсом n-го порядка. Если n =1,
полюс называется простым, в остальных случаях - кратным.
3. Главная часть
содержит бесконечно много членов. В этом случае особая точка а называется
существенно особой точкой.
1.2.2. Признаки особых точек по значению ![]() .
1. Для
того, чтобы особая точка z = a была
устранимой особой точкой функции f(z),
необходимо и достаточно, чтобы существовал конечный предел
.
1. Для
того, чтобы особая точка z = a была
устранимой особой точкой функции f(z),
необходимо и достаточно, чтобы существовал конечный предел ![]() = C, C ≠
∞.
Док-во. Выпишем разложение f(z) в
ряд Лорана:
= C, C ≠
∞.
Док-во. Выпишем разложение f(z) в
ряд Лорана: ![]() . Очевидно,
что
. Очевидно,
что ![]() может
быть конечным тогда и только тогда, когда отсутствуют члены с отрицательными
степенями, т.е. отсутствует главная часть, т.е. z = a – устранимая
особая точка. В этом случае
может
быть конечным тогда и только тогда, когда отсутствуют члены с отрицательными
степенями, т.е. отсутствует главная часть, т.е. z = a – устранимая
особая точка. В этом случае ![]() = A0.
2. Для
того, чтобы особая точка z = a была
полюсом функции f(z), необходимо и достаточно,
чтобы существовал бесконечный предел
= A0.
2. Для
того, чтобы особая точка z = a была
полюсом функции f(z), необходимо и достаточно,
чтобы существовал бесконечный предел ![]() =
∞.
Докажем теорему, из которой
следует это утверждение.
Теорема. Для того, чтобы
особая точка z = a была
полюсом n-го порядка функции f(z),
необходимо и достаточно, чтобы в некоторой окрестности этой точки f(z) представлялась
в виде
=
∞.
Докажем теорему, из которой
следует это утверждение.
Теорема. Для того, чтобы
особая точка z = a была
полюсом n-го порядка функции f(z),
необходимо и достаточно, чтобы в некоторой окрестности этой точки f(z) представлялась
в виде 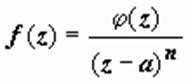 , где φ(z) аналитическая
в точке а функция, φ(a) ≠
0.
Док-во. Необходимость. Пусть f(z) имеет
в точке z = a была полюс n-го
порядка,т.е.
, где φ(z) аналитическая
в точке а функция, φ(a) ≠
0.
Док-во. Необходимость. Пусть f(z) имеет
в точке z = a была полюс n-го
порядка,т.е. 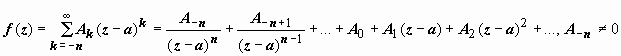 Преобразуем
это выражение:
Преобразуем
это выражение: ![]() .
Обозначим φ(z) сумму ряда, стоящего в скобках:φ(z)
= A -n + A -n +
1(z − a) + A -n +
2(z − a)2 + …
+ A0(z − a) n + A1(z − a) n +
1 + A1(z − a) n +
2 + ….
Ряд Лорана функции f(z) сходится
в некотором кольце 0 < | z – a |
< r. Пусть точка z1 принадлежит
этому кольцу. Ряд для φ(z) сходится в этой
точке, так как он отличается от сходящегося ряда для f(z) только
постоянным множителем
.
Обозначим φ(z) сумму ряда, стоящего в скобках:φ(z)
= A -n + A -n +
1(z − a) + A -n +
2(z − a)2 + …
+ A0(z − a) n + A1(z − a) n +
1 + A1(z − a) n +
2 + ….
Ряд Лорана функции f(z) сходится
в некотором кольце 0 < | z – a |
< r. Пусть точка z1 принадлежит
этому кольцу. Ряд для φ(z) сходится в этой
точке, так как он отличается от сходящегося ряда для f(z) только
постоянным множителем ![]() ; по теореме
Абеля ряд для φ(z) сходится в круге | z – a |
< | z1 – a |,
и φ(z) аналитична в этом круге как сумма
степенного ряда.
Достаточность.
Пусть
; по теореме
Абеля ряд для φ(z) сходится в круге | z – a |
< | z1 – a |,
и φ(z) аналитична в этом круге как сумма
степенного ряда.
Достаточность.
Пусть ![]() , где φ(z) аналитическая
в точке а функция, φ(a) ≠
0. Разложим φ(z) в ряд Тейлора: φ(z)
= B0 + B1(z − a)
+ B2(z − a)2 +
… + Bk(z − a)k +
… . Тогда
, где φ(z) аналитическая
в точке а функция, φ(a) ≠
0. Разложим φ(z) в ряд Тейлора: φ(z)
= B0 + B1(z − a)
+ B2(z − a)2 +
… + Bk(z − a)k +
… . Тогда ![]() , т.е.
главная часть ряда Лорана функции f(z) начинается
с члена
, т.е.
главная часть ряда Лорана функции f(z) начинается
с члена ![]() , где B0 = φ(a)
≠ 0, т.е. точка z = a – полюс n-го
порядка.
Следствие. Точка z = a – полюс n-го
порядка функции f(z) тогда и только
тогда, когда существует конечный
, где B0 = φ(a)
≠ 0, т.е. точка z = a – полюс n-го
порядка.
Следствие. Точка z = a – полюс n-го
порядка функции f(z) тогда и только
тогда, когда существует конечный ![]() .
Теорема о связи нулей и
полюсов. Функция f(z) имеет в
точке z = a – полюс n-го
порядка тогда и только тогда, когда функция
.
Теорема о связи нулей и
полюсов. Функция f(z) имеет в
точке z = a – полюс n-го
порядка тогда и только тогда, когда функция ![]() имеет в
этой точке нуль n-го порядка.
Это теорема непосредственно
следует из доказанной теоремы и теоремы предыдущего раздела. С её помощью легко
определять порядок полюса. Так, мы доказали, что функция
имеет в
этой точке нуль n-го порядка.
Это теорема непосредственно
следует из доказанной теоремы и теоремы предыдущего раздела. С её помощью легко
определять порядок полюса. Так, мы доказали, что функция ![]() имеет в
точке 0 нуль пятого порядка. Поэтому функция
имеет в
точке 0 нуль пятого порядка. Поэтому функция  имеет в
этой точке полюс пятого порядка.
3. Мы
доказали, что в устранимой особой точке и в полюсе существует (конечный или
бесконечный)
имеет в
этой точке полюс пятого порядка.
3. Мы
доказали, что в устранимой особой точке и в полюсе существует (конечный или
бесконечный) ![]() . Поэтому в
существенно особой точке этот предел существовать не может. Более того,
верна теорема Пикара, которую мы приведём без доказательства:
В любой сколь угодно малой
окрестности своей существенно особой точки функция f(z) принимает
(причём бесконечно много раз) любое конечное значение (за исключением,
возможно, одного).
. Поэтому в
существенно особой точке этот предел существовать не может. Более того,
верна теорема Пикара, которую мы приведём без доказательства:
В любой сколь угодно малой
окрестности своей существенно особой точки функция f(z) принимает
(причём бесконечно много раз) любое конечное значение (за исключением,
возможно, одного).
1.3. Вычет аналитической функции в особой точке.
Пусть функция f(z) аналитична
в области D за исключением точки a.
Разложим f(z) в окрестности этой точки в
ряд Лорана: 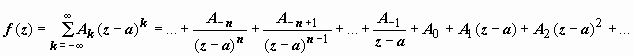 Коэффициент A-1 называется
вычетом функции f( z) в точке а и
обозначается
Коэффициент A-1 называется
вычетом функции f( z) в точке а и
обозначается ![]() . Если γ -
произвольный кусочно-гладкий замкнутый контур, расположенный в области D и
содержащий внутри себя точку а, то, согласно общей формуле для
коэффициентов ряда Лорана (см. 19.8.3. Ряд Лорана), получаем
другое, эквивалентное, определение вычета
. Если γ -
произвольный кусочно-гладкий замкнутый контур, расположенный в области D и
содержащий внутри себя точку а, то, согласно общей формуле для
коэффициентов ряда Лорана (см. 19.8.3. Ряд Лорана), получаем
другое, эквивалентное, определение вычета
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.