Изолированные особые точки аналитической функции. Вычеты. Вычет аналитической функции в особой точке

Первая отличная от нуля производная функции в точке a = 0 - пятая, поэтому эта точка - нуль пятого порядка функции .   Теорема. Для того, чтобы аналитическая в точке а функция f(z) имела в этой точке нуль k -го порядка, необходимо и достаточно, чтобы в окрестности этой точки функция f(z)представлялась в виде f( z) = (z − a) ^k·φ(z), где φ(z) - аналитическая в точке а функция, и φ(a) ≠ 0.   Доказательство. Необходимость. Пусть точка а - нуль k-го порядка функции f(z), т.е. f(a) = f ′(a) = f ″(a) = ... = f ^(k−1)(a) = 0, и f ^(k)(a) ≠ 0. Тогда её разложение в ряд Тейлора имеет вид 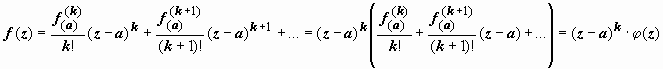, где 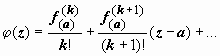 - аналитическая (как сумма степенного ряда с тем же кругом сходимости, что и у ряда для f(z)) функция, 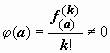.   Достаточность. Пусть f( z) = (z − a) ^k·φ(z), где φ(z) - аналитическая в точке а функция, и φ(a) ≠ 0. Находим производные этой функции по формуле Лейбница( uv ) ⁽ⁿ⁾ = u ⁽ⁿ⁾ v + n u ^{(n - 1)} v ′ + C_n² u ^{(n - 2 )} v ″ + C_n³ u ^{(n - 3 )} v^{(3 )} + … + C_n² u ″ v ^{(n - 2)} + n u ′ v ^{(n - 1 )} + u v ^(n ): f ′(z) = k(z − a)^{k - 1} φ(z) + (z − a)^k φ ′(z), f ′(a) = 0; f ″(z) = k (k − 1)(z − a)^{(k - 2)} φ(z) + 2k (z − a)^{(k - 1)} φ′(z) + (z − a)^(k) φ″(z), f ″(a)=0;  f ^{( k -1 )}(z) = k·( k -1 )·…2·(z − a) φ(z) + C¹_k-1k·( k -1 )·…3·(z − a)² φ ′(z) + … + (z − a) ^k φ^(k -1)(z), f ^( k -1)(a)=0;  f ^( k)(z) = k·( k -1 )·…2·1·φ(z) + C¹_k k·( k -1 )·…2·(z − a) φ ′(z) + … + (z − a) ^k φ^(k)(z), f ^( k)(a) = k!·φ(a) ≠ 0, что и требовалось доказать.   Из этой теоремы следует, что если многочлен P _n(z) = a₀ z ⁿ + a₁ z ^{n - 1} + a₂ z ^{n - 2} + … + a _{n - 1} z = 0 разложен на множители P _n(z) = a₀ (z − z₁) ^k₁ (z − z₂) ^k₂ … (z − z_l) ^k_l , то корни z₁, z₂, …, z_lявляются нулями функции P _n(z) кратностей, соответственно, k₁, k₂, …, k_l. 

 1.2. Изолированные особые точки.   1.2.1. Определение. Точка а называется изолированной особой точкой функции f(z), если существует окрестность этой точки, в которой f(z) аналитична во всех точках, за исключением точки а.   Рассмотрим разложение функции f(z) в ряд Лорана 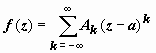 в окрестности изолированной особой точки а. При этом возможны следующие случаи.   1. Главная часть ряда Лорана отсутствует: 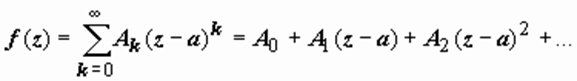.   В этом случае особая точка а называется устранимой.   2. Главная часть содержит конечное число членов: .   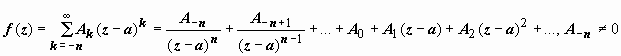В этом случае особая точка а называется полюсом n-го порядка. Если n =1, полюс называется простым, в остальных случаях - кратным.   3. Главная часть содержит бесконечно много членов. В этом случае особая точка а называется существенно особой точкой. 

 1.2.2. Признаки особых точек по значению .   1. Для того, чтобы особая точка z = a была устранимой особой точкой функции f(z), необходимо и достаточно, чтобы существовал конечный предел  = C, C ≠ ∞.   Док-во. Выпишем разложение f(z) в ряд Лорана: . Очевидно, что  может быть конечным тогда и только тогда, когда отсутствуют члены с отрицательными степенями, т.е. отсутствует главная часть, т.е. z = a – устранимая особая точка. В этом случае  = A₀.   2. Для того, чтобы особая точка z = a была полюсом функции f(z), необходимо и достаточно, чтобы существовал бесконечный предел  = ∞.   Докажем теорему, из которой следует это утверждение.   Теорема. Для того, чтобы особая точка z = a была полюсом n-го порядка функции f(z), необходимо и достаточно, чтобы в некоторой окрестности этой точки f(z) представлялась в виде 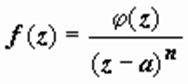, где φ(z) аналитическая в точке а функция, φ(a) ≠ 0.   Док-во. Необходимость. Пусть f(z) имеет в точке z = a была полюс n-го порядка,т.е. 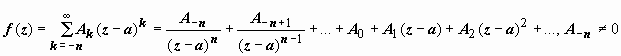Преобразуем это выражение: . Обозначим φ(z) сумму ряда, стоящего в скобках:φ(z) = A _-n + A _{-n + 1}(z − a) + A _{-n + 2}(z − a)² + … + A₀(z − a) ⁿ + A₁(z − a) ^{n + 1} + A₁(z − a) ^{n + 2} + ….   Ряд Лорана функции f(z) сходится в некотором кольце 0 < | z – a | < r. Пусть точка z₁ принадлежит этому кольцу. Ряд для φ(z) сходится в этой точке, так как он отличается от сходящегося ряда для f(z) только постоянным множителем ; по теореме Абеля ряд для φ(z) сходится в круге | z – a | < | z₁ – a |, и φ(z) аналитична в этом круге как сумма степенного ряда.   Достаточность. Пусть , где φ(z) аналитическая в точке а функция, φ(a) ≠ 0. Разложим φ(z) в ряд Тейлора: φ(z) = B₀ + B₁(z − a) + B₂(z − a)² + … + B_k(z − a)^k + … . Тогда , т.е. главная часть ряда Лорана функции f(z) начинается с члена , где B₀ = φ(a) ≠ 0, т.е. точка z = a – полюс n-го порядка.   Следствие. Точка z = a – полюс n-го порядка функции f(z) тогда и только тогда, когда существует конечный .   Теорема о связи нулей и полюсов. Функция f(z) имеет в точке z = a – полюс n-го порядка тогда и только тогда, когда функция  имеет в этой точке нуль n-го порядка.   Это теорема непосредственно следует из доказанной теоремы и теоремы предыдущего раздела. С её помощью легко определять порядок полюса. Так, мы доказали, что функция  имеет в точке 0 нуль пятого порядка. 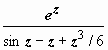Поэтому функция  имеет в этой точке полюс пятого порядка.   3. Мы доказали, что в устранимой особой точке и в полюсе существует (конечный или бесконечный) . Поэтому в существенно особой точке этот предел существовать не может. Более того, верна теорема Пикара, которую мы приведём без доказательства:   В любой сколь угодно малой окрестности своей существенно особой точки функция f(z) принимает (причём бесконечно много раз) любое конечное значение (за исключением, возможно, одного). 

 1.3. Вычет аналитической функции в особой точке. 

Пусть функция f(z) аналитична в области D за исключением точки a. Разложим f(z) в окрестности этой точки в ряд Лорана: 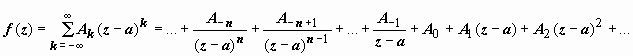   Коэффициент A_-1 называется вычетом функции f( z) в точке а и обозначается . Если γ - произвольный кусочно-гладкий замкнутый контур, расположенный в области D и содержащий внутри себя точку а, то, согласно общей формуле для коэффициентов ряда Лорана (см. 19.8.3. Ряд Лорана), получаем другое, эквивалентное, определение вычета