Металлический терморезистор: назначение, принцип действия, конструкция. Представление устройства в виде структурной схемы, страница 3

Y                         X                                         Q                       Z                            W

W3

W3

W2

W1

  

Рисунок 6

Где W₁...W₄ – передаточные функции соответствующих звеньев.

3 Общие сведения об основных характеристиках систем с распределёнными параметрами (СРП)

Основной характеристикой СРП является континуальная передаточная функция. Она показывает отношение выходной функции к входной (по Лапласу) в привязке к конкретной точке.

В искомой задаче выходная функция обозначается буквой Q(х,t), где x - трехмерная переменная в декартовых, полярных, цилиндрических или сферических координатах, f(x,t) - входная координата по среде, зависящая от трехмерной координаты х и времени t. Основное уравнение задачи записывается в виде:        l(Q(х,t)) = f(х,t), xD, t≥t₀, где l - оператор дифференциального уравнения - формула преобразования выходной величины Q.

В каждой задаче определяются граничные или краевые условия:

Г(Q(х,t))=g(х,t); xD, t>t₀,

где Г - оператор граничных или краевых условий, g - входное воздействие на границе в каждый момент времени.

Для того чтобы решить задачу во всей области координат, необходимо знать ее значения в каждой точке по границе области.

Начальные условия для задачи записываются в виде:

N(Q(х,t))= Q₀(х); xD, t=t₀,

где: N - оператор начальных условий; Q₀(х) - значение искомой функции в заданный момент времени.

Для того чтобы решить задачу во всей области координат, необходимо знать её значения в каждой точке пространства x. Получили систему:

l(Q(х,t)) = f(х,t), xD, t≥t₀,

Г(Q(х,t))= g(х,t); xD, t>t₀,                                                                                                (1)

N(Q(х,t))= Q₀(х); xD, t=t_0.

Необходимо знать:

1 Значение функции на границе в каждый момент времени

2 Значение в каждой точке области в момент времени t₀.

В указанном виде (1) система практически не разрешима. Для ее решения вводится в рассмотрение стандартная форма записи (2). Она подразумевает нулевые граничные и начальные условия. Ее вид:

l(Q(х,t)) =ω(х,t), xD, t≥t₀,

Г(Q(х,t))=0; xD, t>t₀,                                                                                                (2)

N(Q(х,t))=0; xD, t=t₀,

где ω(х,t) - стандартизующая функция ω(х,t)= f(х,t)

При Г=0, N=0 - входное воздействие на систему при нулевых граничных и начальных условиях и первая из трех основных функций, которая понадобится при решении (берется из справочника).

Второй функцией является функция Грина (импульсная переходная функция, функция влияния, функция источника, функция веса). Функцией Грина называется функция источника, которая равна выходному сигналу G(x,t) = Q(x,t) при f(х,t)= δ(х - ξ) δ(t - τ), где δ(х - ξ) - пространственная δ-функция по координатам x,y,z, δ(t - τ) - функция по времени; х - координаты входного возмущения; ξ- координаты точки отклика от удара.

С учетом этого стандартная задача (2) перепишется в виде:

l(G(х,ξ,t,τ)) = δ(х - ξ) δ(t - τ),

Г(G(х, ξ,t,τ))=0;                                                                                                (3)

N(G(х, ξ,t,τ))=0;

где функция Грина от G(x,t) берется из справочника.

Зная эти две характеристики можно найти выходную функцию по следующему выражению:       

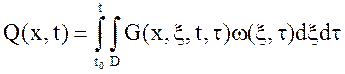                                                                                                (4)

Если задача статическая, то есть отсутствует уравнение времени t, то ее можно записать в виде

l(Q(х)) = f(х), xD,

Г(Q(х))= g(х); xD,                                                                                                (5)

N≡0_.

Стандартная форма записи будет выглядеть как:

l(Q(х)) = ω(х), xD,

Г(Q(х))= 0; xD,                                                                                                (6)

при однородных (нулевых) граничных условиях.

Функция Грина такой задачи удовлетворяет системе уравнений:

l(G(х,ξ)) = δ(х - ξ) δ(t - τ), xD, ξD,

Г(G(х,ξ))=0;                                                                                                (7)

х- координаты возмущения, ξ - координаты отклика.

Решение задачи в этом случае выглядит следующим образом

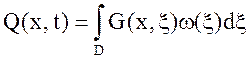                                                                                                (8)

Бывают задачи, в которых отсутствуют пространственные координаты, т.е. процесс во времени. В таком случае задача записывается следующим образом:

l(Q(t)) = f(х,t), xD, t≥t₀,

N(Q(t))= Q₀.                                                                                                (9)

Стандартная форма записи:

l(Q(t)) = ω(t), t≥t₀,

N(Q(t))= 0.                                                                                              (10)

Функция Грина:

l(G(t,τ)) = δ(t - τ),

N(G(t, τ))=0;                                                                                              (11)

Решение такой задачи имеет вид:

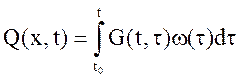                                                                                              (12)

Для управления и синтеза системы управления, исходя из ТАУ, необходимо знать передаточную функцию. В теории СРП вводится понятие континуальной передаточной функции, т.е. точечной передаточной функции в пределах области D, когда возмущение подается на среду в точке х, а реакция регистрируется в точке ξ.

Континуальная передаточная функция выражается следующим образом:

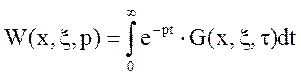                                                                                              (13)

По сути, континуальная передаточная функция - это преобразование Лапласа функции Грина, т.е. при этих функциях континуальная передаточная функция является производной и всегда может определиться по функции Грина.

Таким образом, для решения задачи по CРII необходимо знать две функции: нормирующую функцию и функцию Грина