Влияние примесей и дефектов кристаллической решетки. Наличие примесей или дефектов кристаллической решетки увеличивает частоту соударений; к числу соударений, обусловленных тепловыми колебаниями, nс(Т), прибавляется число столкновений, обусловленных примесями внедрения и дефектами кристаллической решетки nc(i):
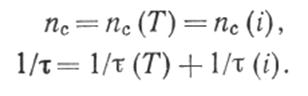
Предыдущее выражение для удельного сопротивления распадается соответственно на два члена:
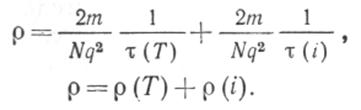
При очень низких температурах ρ(T)<<ρ(i), т. е. удельное сопротивление перестает зависеть от температуры и зависит только от концентрации примесей и дефектов кристаллической решетки металла. В этом состоит правило Маттисена.
Чувствительность к температуре ар определяется соотношением
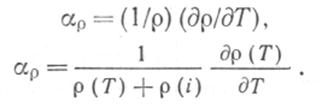
Наличие атомов внедрения или структурных дефектов, учитываемое членом p(i) приводит к снижению чувствительности. Этим объясняется важность чистоты металлов и отсутствия внутренних напряжений для обеспечения максимальной, и строго определенной чувствительности к температуре.
Зависимость сопротивления от температуры.
Платина. В диапазоне температур приблизительно от -200 до 650°С по величине сопротивления проволоки из очень чистой платины можно определить температуру (с погрешностью, не превышающей -0,1°С) по формуле Календара - ван Дюсена:
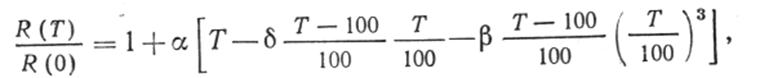
где Т выражается в °С и β=0 при T>0°С. Экстраполяция этой формулы до температуры затвердевания золота, равной 1064.43 °С при нормальном атмосферном давлении, приводит к погрешностям, не превышающим 2°С. Формула Календари - ван Дюсена эквивалентна соотношению
где A=α(1+δ/100), В=-αδ*104, С=-αβ*10-8 при T<0°С и С=0 при T>0°С. Четыре значения сопротивления К, измеренные при точно известных температурах, позволяют определить требуемые характеристики. Здесь R(0) - сопротивление, измеренное при температуре 0°С; α вычисляется по предыдущей величине и сопротивлению, измеренному при температуре 100°C: а=[R(100)-R(0)]/100R(0); δ можно вычислить, измерив сопротивление, например, при температуре кипения серы (444,4 °С при нормальном атмосферном давлении).
Величина β определяется путем измерений при низкой температуре, обычно при температуре кипения кислорода (-182,97°С при нормальном атмосферном давлении).
Для резисторов из платины высокой чистоты, не имеющей внутренних механических напряжений, изготовитель датчиков (фирма Rosemount) приводит следующие значения: α=0,00392, β=1,492, δ=0,11 при T<0°С и β=0 при Т>0°С. Отсюда A=3,90802*10-3; В=5,80195*10-7; С=-4,27350*10-12 при T<0°С и С = 0 при T>0°С.
Сопротивление из никеля. В диапазоне температур от -60 до +70°С зависимость сопротивления никеля от температуры удовлетворительно описывается формулой
где Т выражается в °С, R0 - сопротивление при температуре 0°С, А=5,49167*10-3 0С и В=6,666667*10-6 0C-1.
В стандарте DIN 43760 приведен ряд значений сопротивления в диапазоне температур от -60 до 180 0С, а также величины допусков.
Зависимость
электрического сопротивления проводника от его температуры выражается формулой:
, где θ – температура проводника; R0 – сопротивление проводника при температуре θ0;
φ(θ-θ0) - определенная функция разности температур. В широком диапазоне
температур функция φ(θ-θ0) хорошо аппроксимируется экспоненциальной
зависимостью φ(θ-θ0)=e-α(θ-θ0).
В узком диапазоне температур функция φ(θ-θ0) с достаточной точностью аппроксимируется полиномом φ(θ-θ0)=1+α(θ-θ0)+β(θ-θ0)2+…
Коэффициенты α, β, … в выражениях определяются экспериментально.
Получим зависимость температуры проводника θ от температуры среды τ, в которой он находится. Для этого вычислим изменение количества тепла dQ, содержащегося в проводнике, при изменении его температуры на dθ: dQ=mc*dθ, где с – теплоемкость материала проводника, m – его масса. С другой стороны, согласно закону Ньютона, количество тепла, получаемое датчиком от внешней среды, пропорционально разности температур среды и датчика, площади поверхности датчика и времени:dQ=kS(τ-θ)dt, где k – коэффициент теплоотдачи. На основании закона сохранения энергии левые части в уравнениях равны. Поэтому вытекает дифференциальное уравнение, связывающее температуру датчика θ и температуру среды τ: T θ+θ=τ, где T=cm/kS – постоянная времени термосопротивления. На основании полученных уравнений термосопротивление можно представить в виде последовательного звена и нелинейности с экспоненциальной или квадратичной характеристикой.
 |
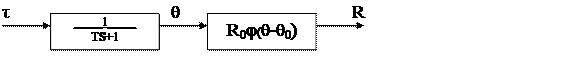Рисунок 4
Используя приведенные выше уравнения и табличные данные получим:
T=cm/kS=0.13*0.02/20*0.005=0.026
За начальное сопротивление проводника примем (температура 200С)
4.3 кОм.
Таким образом передаточная функция запишется в виде:
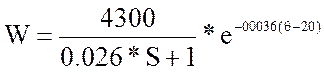
2 Представление устройства в виде структурной схемы
Для представления металлического терморезистора в виде отдельных блоков рассмотрим структурную схему одного из видов терморезистора (рисунок 1) и физику устройства.
Самое общее, что можно привести по физике устройства, это влияние температуры на удельное сопротивление металла и тем самым на сопротивление участка металла в целом. Регистрирующий элемент фиксирует изменение сопротивления тем самым, сообщая об изменении его температуры, а значит, температуры тела в котором находится терморезистор.
Представим вышеизложенное в виде схемы (рисунок 5), на которой были выделены ССП и СРП.
Рисунок 5
Где: t1-температура на корпусе блока, предполагается, что совпадает с температурой исследуемой среды;
t2-температура нити терморезистора, лишь через некоторый промежуток времени будет приравнена t1;
R-текущее сопротивление нити, предполагается зависимость от температуры, но не от приращения температуры;
B-индукция магнитного поля, вообще говоря не является единственной выходной величиной данного блока, однако играет более значительную роль для следующего блока;
α-угол поворота регистрирующего органа, является единственной визуальной характеристикой для определения температуры в данном устройстве.
Можно также для большей наглядности представить рисунок 5 в виде передаточных функций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.