Площадь бетона A =Аb,tоt+αАs=bf’·hf’+b(h-hf’)
А= 1440·50+200·(300-50)=72000+50000=122000 мм2
Вычисляем площадь приведенного сечения смотри (рисунок 5).
Ared = A+αAsp = 12200+6,67 628=126188 мм2
Статический момент приведенного сечения относительно нижней растянутой грани S red= bf’·hf’·(h-0,5·hf’)+b·(h-hf’)·0,5·(h-hf’)+ αAsp·a=
72000·(300-25)+50000·0,5(300-50)+ 6,67·628·40= 26217550мм3;
Момент инерции приведенного сечения
Ired =I+αysp =b(h-hf’)3 /12+b(h-hf’)y12+bf’hf’3/12+bf’hf’y22+αAspysp2=
= 1440(300-50)3/12+1440(300-50)1682+1440·503 /12+1440·50·672+6,67·628·1682=
=11,23·108мм4
Момент сопротивления приведенного сечения по нижней грани
Wred =Ired /yo=11,23·108/208=0,05·108
Момент сопротивления приведенного сечения по верхней грани
Wred' =Ired /(ho-yo)=11,23·108/(260 -208)=9·108
Упругопластические моменты сопротивления
Wpl =γWred= 1,75·0,05·108 =0,09·108
Wpl' =γWred' =1,75·9·108 =15,8·108
здесь γ=1,75 для таврового сечения с полкой в сжатой зоне.
Рассчитываем расстояние от ЦТ приведенного сечения до ядровых точек верхней: r =ᵠn( Wred/Ared)=0,85(0,05·108/ 126188)=34
нижней: rlnf =ᵠn ( Wred' /Ared)=0,85(9·108/ 126188)=6062
здесь In=1,6-σsp/ Rb,ser=1,6-0,75=0,85 σsp/ Rb,ser=0,75
2.5 Определение потерь предварительного напряжения
Согласно п.2.25 [1], максимально допустимое значение σspбез учета потерь равно σsp=0,9Rs,n=0,9·600 =540 МПа.
Определим первые потери.
Потери от релаксации напряжений в арматуре согласно п.2.27[1] равны
Δσsp1 = 0,03σsp = 0,03·540 = 16 МПа.
По агрегатно-поточной технологии изделие при пропаривании нагревается вместе с формой и упорами, поэтому температурный перепад между ними равен нулю и, следовательно, Δσsp2 = 0.
Потери от деформации формы Δσsp3 и анкеров Δσsp4 при электротермическом натяжении арматуры равны нулю.
Таким образом, сумма первых потерь равна Δσsp(1) = Δσsp1 = 16 МПа, а усилие обжатия с учетом первых потерь равно
P(1) = Asp (σsp - Δσsp(1)) = 628(540-16) = 329072 Н.
В связи с отсутствием в верхней зоне напрягаемой арматуры
(т.е. при A'sp = 0) из формулы (2.10 [7]) имеем e0p1=ysp=168 мм.
В соответствии с п. 2.34 [1] проверим максимальное сжимающее напряжение бетона σbp от действия усилия Р(1), вычисляя σbp по формуле (2.8 [1]) при ys=ysp=168 мм и принимая момент от собственного веса М равным нулю:
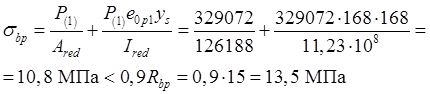
где 
-передаточная прочность
бетона Rbp=0,5 B=0,5 25=12,5МПа принимаем согласно п.2.34[1] 
, где В
–класс бетона т.е. требование п.2.34[1] выполняется.
Определяем вторые потери напряжений согласно пп.2.31 и 2.32[1]
Потери от усадки равны Δσsp5=0,0002·2·105=40МПа.
Потери от ползучести определяем по формуле (2.7[1]), принимая значения φb,сr и Еb по классу бетона В25 (согласно табл.2.6[1] φb,сr=2,3 согласно табл.2.5[1] Еb=2,75·105 МПа; α=Es/Eb=6,67
Определим напряжение бетона на уровне арматуры Sпо формуле 2.8[1]
при ys=ysp=168мм. Для этого определяем нагрузку от веса половины плиты см.п.2.12[1]
и момент от этой нагрузке в середине пролета
(здесь l=5,7 м – расстояние между прокладками при хранении плиты); тогда
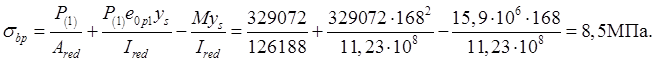
Напряжение бетона на уровне арматуры S' (т.е. при уs=уs2 =67мм)
Потери от ползучести
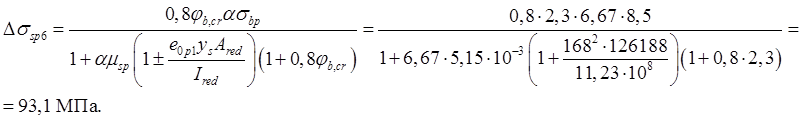
Вторые потери для арматуры равны
Δσsp(2)=Δσsp5 +Δσsp6 =40 + 93,1=133,1 МПа.
Суммарная величина потерь напряжения
Δσsp(1) +Δσsp(2) =16 +133,1=149,1 МПа >100 МПа, следовательно, требование п.2.36 [1] выполнено и потери не увеличиваем.
Напряжение Δσsp2с учетом всех потерь равно
Δσsp2=540 -149,1=390,9 МПа.
Усилие обжатия с учетом всех потерь напряжений Р определяем по формуле (2.17[1]).
Р =Δσsp2 Asp = 390,9·628=245485Н=245кН;
Проверяем достаточность размеров принятого сечения ребер для обеспечения прочности по бетонной полосе между наклонными сечениями по условию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.