Применение микроэкономических моделей к анализу структуры рынка нефтепродуктов Волгоградской области, страница 3

Индекс Лернера может принять значение в пределах от нуля до единицы. В условиях совершенной конкуренции, индекс равен нулю, и цена равна предельным издержкам. Чем сильнее рыночная власть фирмы в данном секторе экономики, тем более значения индекса приближается к единице.

Рыночная власть не гарантирует высокую норму прибыли, поскольку прибыль зависит от соотношения цены и средних издержек, а не предельных. Фирма может обладать высокой монопольной властью, но получать меньшую прибыль, так как средние издержки этой фирмы значительно выше.

Данные по предельным издержкам производства трудно получить в процессе исследований. Однако, известно, что в долгосрочном периоде в условиях равновесия предельные издержки равны средним[3]. Это позволяет преобразовать индекс Лернера (5):

(6)

В форме записи (6) индекс Лернера фактически представляет отношение прибыли монополиста к объему реализованной продукции по рыночной цене:

(7)

Следовательно, чем выше удельный вес прибыли в объеме реализации продукции, тем выше степень монопольной власти на рынке. Некоторые экономисты считают, что высокая норма прибыли есть признак наличия на рынке монопольной власти.

Если модифицировать формулу (7) следующим образом:

(8)

то индекс Лернера можно использовать для оценки соотношения цены и прибыли на единицу продукции.

Глава 2. Модификация индекса Лернера для случая нескольких и возможности его применения для описания олигополии

На олигополистическом рынке также существует связь между индексом Лернера, ценовой эластичностью и степенью рыночной власти, однако она более сложная.

Рассмотрим олигополистический рынок одного товара. Примем следующие обозначения[4]:

n –количество фирм-производителей;

i – номер фирмы, 1 ≤ i≤nнезависимые переменные;

– объем выпуска i-ой фирмы, 1 ≤ i≤nнезависимые переменные;

P–среднеотраслевая цена;

P= P(Q) – обратная функция отраслевого спроса;

– функции краткосрочных издержек фирм-производителей;

– функции чистой прибыли i-ой фирмы;

– показатель Лернера, а точнее монопольная власть i-ой фирмы;

L – среднеотраслевой показатель, характеризующий монопольную власть. – доля i-ой фирмы в совокупной объеме;

– эластичность отраслевого спроса по цене; 

;

–отраслевой коэффициент ценовой эластичности спроса;

Аналогично, ценовая эластичность и коэффициент ценовой эластичности спроса для i-ой фирмы.

Учтем следующие гипотезы:

1.  Товар нормальный

2.  Функции издержек и отраслевого спроса линейны:  

Где – постоянные издержки;

– предельные издержки.

3.  Допустим, что каждый производитель максимизирует собственную прибыль, выбирая объем выпуска независимо от конкурентов. 

Рассмотрим задачу максимизации чистой прибыли i-ой фирмы:

Необходимое условие максимизации:

С учетом того, что 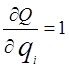, необходимое условие будет иметь следующий вид:

Достаточное условие максимизации чистой прибыли имеет вид

Оно выполняется, так как функция спроса линейна, и товар нормальный. Отсюда имеем:

Левая часть этого соотношения представляет собой коэффициент монопольной власти Лернера[5] для i-ой фирмы:

(9)

Таким образом, монопольная власть отдельного олигополиста зависит не только от ценовой эластичности, но и от его доли на рынке.

Отметим, коэффициент Лернера для i-ой фирмы прямо пропорционален доле i-ой фирмы в совокупном объеме и обратно пропорционален среднеотраслевому коэффициенту ценовой эластичности:

(10)

Показатель монопольной власти Лернера численно равен превышению цены над предельными издержками, выраженному как доля в цене. Его значение показывает прибыльность бизнеса, а в нефтяном секторе показывает уровень ренты в цене.принимает значения от 0 до 1. Чем ближе к 1, тем выше степень монопольной власти.По формуле (9) очевидно, что, то есть только рынки с эластичным спросом может обслуживать монополия без государственного регулирования.