Методические указания по расчету открытых конических передач. Допускаемые напряжения для расчета на выносливость при изгибе, страница 6

Для колеса              N_FE2 = μ_FE  · N_∑2 = 0,14·14,4·10⁶ = 2,016·10⁶.

5.2.3 Материалы зубчатых колес

Шестерня изготавливается из стали 45 по ГОСТ 1050 (см. таблицу 1).

Термообработка – улучшение,  твердость НВ₁ 235–262, предел прочности σ_В1 = 780 МПа, предел текучести σ_Т1 = 540 МПа.

Колесо изготавливается также из стали 45 (см. таблицу 1).

Термообработка – нормализация, твердость НВ₂ 179–207, предел прочности σ_В = 600 МПа, предел текучести σ_Т = 320 МПа.

Средние твердости поверхностей зубьев шестерни и колеса:

5.2.4 Допускаемые напряжения

5.2.4.1 Допускаемые напряжения для расчета на изгибную выносливость

1) Для шестерни

,

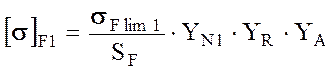- предел изгибной выносливости  для материала шестерни при отнулевом цикле:

 = 1,75×HB_ср1=1,75×248,5=434,875 МПа,

S_F = 1,75– коэффициент запаса прочности при расчете на изгибную прочность (см. с.7);

 – коэффициент долговечности  для шестерни, учитывающий влияние ресурса передачи:

 ,

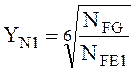здесь = 4·10⁶ – базовое число циклов перемены напряжений (см. с.7), так как > , следовательно, (см. с.7);

 – коэффициент, учитывающий влияние шероховатости переходной поверхности между зубьями, который принимают:  при шлифовании или зубофрезеровании с параметрами шероховатости  мкм, что характерно для открытых передач (см. с.7);

 – коэффициент, учитывающий влияние двухстороннего приложения нагрузки (реверса): при одностороннем  приложении нагрузки (при нереверсивном движении)  (см. с.7).

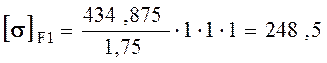Тогда:   МПа.

2) Для колеса

,

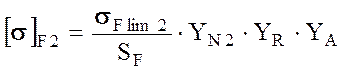- предел изгибной выносливости  для материала колеса при отнулевом цикле:

 = 1,75×HB_ср2=1,75×193=337,75 МПа;

 – коэффициент долговечности  для колеса, учитывающий влияние ресурса передачи:

 ,

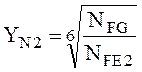так как < ,  то коэффициент долговечности равен:

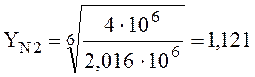 (см. с.7);

Тогд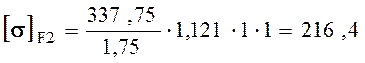а:   МПа.

5.2.4.2  Предельные допускаемые напряжения для расчета на изгибную выносливость

Для шестерни:

[σ]_Fmax1 = 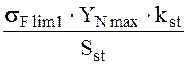, МПа, где  максимально возможное значение коэффициента долговечности:  (см. с.7);

k_st  - коэффициент влияния частоты приложения пиковой нагрузки, в случае единичных перегрузок принимаем k_st=1,2 (см. с.8);

S_st - коэффициент запаса прочности:  S_st=1,75 (см. с.8).

Тогда  [σ]_Fmax1 = 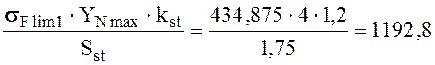 МПа.

Для колеса:

[σ]_Fmax1 = 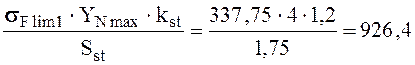 МПа.

5.3  Числа зубьев колес и передаточное число

5.3.1 Число зубьев шестерни

Принято  Z₁ = 17 (см. с.8).

5.3.2 Число зубьев колеса

Z₂ = Z₁ · = 17·2,8 = 47,6.

Принято Z₂ = 48.

5.3.3 Фактическое передаточное число

 .

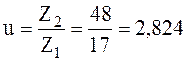5.4  Углы делительных конусов колес

Угол делительного конуса шестерни

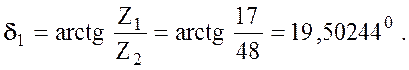
Угол делительного конуса колеса

δ₂ = 90⁰ – δ₁ = 90⁰ – 19,50244⁰ = 70,49756⁰.

5.5  Коэффициент ширины зубчатого венца

5.5.1 Коэффициент ширины зубчатого венца относительно внешнего конусного расстояния

Принято ψ_bRe = 0,285 по ГОСТ 12289 (см. с.8).

5.5.2 Коэффициент ширины венца шестерни относительно среднего делительного диаметра

 .

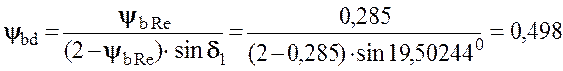5.6  Коэффициент концентрации нагрузки

Принимая, что валы передачи опираются на роликовые подшипники и :        K_Fβ ≈ 1,60  (см. с.8, таблицу 4).

5.7  Коэффициент, учитывающий форму зуба

          Принимается в зависимости от эквивалентного числа зубьев

 .

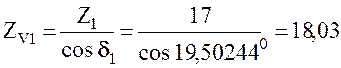Тогда коэффициент формы зуба равен: Y_F1 = 4,2  (см. таблицу 5).

5.8  Предварительное значение среднего окружного модуля

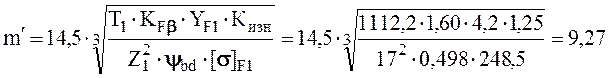 мм, здесь К_изн=1,25 - коэффициент износа при  10% износе (см. таблицу 6).

5.9  Уточнение величины внешнего и среднего модуля

5.9.1 Средний делительный диаметр шестерни

 мм.

5.9.2 Ширина венца

 мм.

По ГОСТ6636 принято b = 80 мм.

5.9.3 Коэффициенты ширины венца

Относительно среднего делительного диаметра шестерни

.

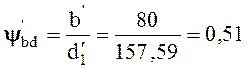Относительно внешнего конусного расстояния

.

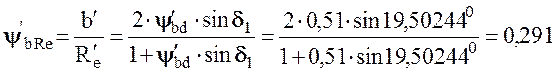5.9.4 Внешнее конусное расстояние

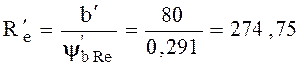 мм.

5.9.5 Среднее конусное расстояние

 мм.

5.9.6 Внешний окружной модуль

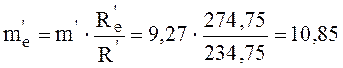 мм.

По ГОСТ 9563 принято m_e = 11 мм (см. с.10).

5.9.7 Внешнее конусное расстояние

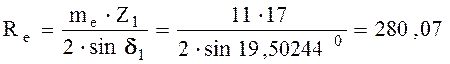 мм.

5.9.8 Ширина венца

b = ψ`_be · R_e = 0,285 · 280,07= 79,82 мм.

Принято b = 80 мм.

5.9.9 Среднее конусное расстояние

R = R_e – 0,5·b = 280,07 – 0,5·80  =  240,07 мм.

5.9.10 Средний окружной модуль

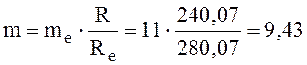 мм.

5.10   Расчетное напряжение изгиба

5.10.1 Коэффициент, учитывающий форму зуба

Y_F1 = 4,2  (см.п.5.7).