Методические указания по расчету открытых конических передач. Допускаемые напряжения для расчета на выносливость при изгибе, страница 5

4.2.7 Уточнение значения среднего конусного расстояния

R = R_e – 0,5·b.

4.2.8 Уточнение значения среднего окружного модуля

 .

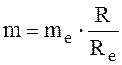Основные геометрические размеры передачи представлены на рисунке 1.

4.3 Проверочные расчеты передачи

4.3.1 Определение коэффициентов формы зубьев шестерни Y_F1 и колеса Y_F2

Предварительно находится эквивалентное число зубьев шестерни Z_V1 и колеса Z_V2:

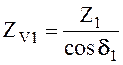 и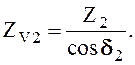 

По таблице 5 уточняются коэффициенты формы зубьев.

 

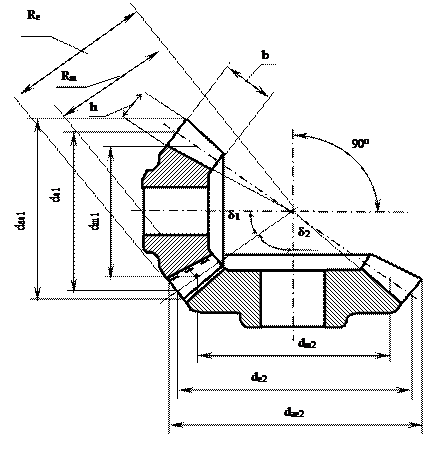Рисунок 1 - Основные геометрические размеры конической зубчатой передачи

4.3.2 Сравнительная оценка прочности зубьев на изгиб

Для шестерни  ,  МПа.

Для колес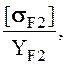а  МПа.

       Из пары сопряженных колес расчет производится по колесу с меньшим отношением [σ]_F / Y_F .

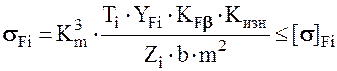 , здесь i – индекс, соответствующий значениям моментов, коэффициентов формы зубьев, числа зубьев для шестерни (i =1)  и колеса (i =2) соответственно.

Отклонение расчетного значения напряжений изгиба  от допускаемого:

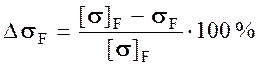, должно быть в пределах  -5 % ≤ ∆σ_F  ≤ +15 % (знак «-» означает недогрузку и знак  «+» означает перегрузку передачи по напряжениям изгиба).

4.4 Проверка передачи на кратковременную пиковую нагрузку

Проверка выполняется при отсутствии в приводе предохранительных муфт и ременных передач.

Коэффициент перегрузки привода:

.

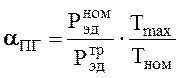Максимальные напряжения изгиба

< [σ]_Fmax1;

< [σ]_Fmax2 .

4.5 Определение основных геометрических размеров колес передачи

4.5.1 Внешние делительные диаметры колес

d_e1 = m_e · Z₁ ;

d_e2 = m_e · Z₂ .

               4.5.2 Внешнее конусное расстояние

 .

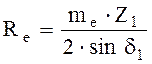4.5.3 Ширина венца

b = ψ`_be · R_e.

4.5.4 Среднее конусное расстояние

R = R_e – 0,5·b.

4.5.5 Средние делительные диаметры колес

d₁ = m · Z₁;

d₂ = m · Z₂.

4.5.6 Внешняя высота головки зуба

h_ae1 = h_ae2 = m_e .

4.5.7 Средняя высота ножки зуба

h_f1 = h_f2 = 1,25·m .

4.5.8 Угол ножки зуба

Для шестерни    .

Для колеса         .

4.5.9 Внешние диаметры вершин зубьев

d_ae1 = d_e1 + 2·m_e·cos δ₁ ;

d_ae2 = d_e2 + 2·m_e·cos δ₂ .

4.5.10 Внешние диаметры вершин зубьев после притупления кромки

 d_ae1 - 2· m_e·sinδ₁;

d_ae2 - 2· m_e·sinδ₂ .

Величины    и   следует округлить до целого числа.

4.5.11 Внешняя высота ножки зуба

h_fe2 = h_fe1 = 1,25·m_e .

4.5.12 Внешняя высота зуба

h_e1 = h_ae1 + h_fe1;

h_e2 = h_ae2 + h_fe2 .

4.5.13 Угол конуса впадин

δ_f1 = δ₁ – θ_f1;

δ_f2 = δ₂ – θ_f2 .

4.6 Силы, действующие в зацеплении

4.6.1 Окружная сила на среднем делительном диаметре шестерни и колеса

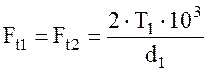, H, где  – вращающий момент на колесе (Н×м);

 – средний делительный диаметр колеса (мм).

4.6.2 Осевая сила на шестерне, равная радиальной силе на колесе

F_a1 = F_r2 = F_t1 ×tg α × sin δ ₁, Н,                

где α – угол профиля производящего (режущего) инструмента α=20⁰ [1, с.24].

4.6.3 Радиальная сила на шестерне, равная осевой силе на колесе

F_r1  = F_a2  = F_t1 × tg α × cos δ ₁ , Н.

Силы, действующие в коническом зацеплении, представлены на рисунке 2.

 

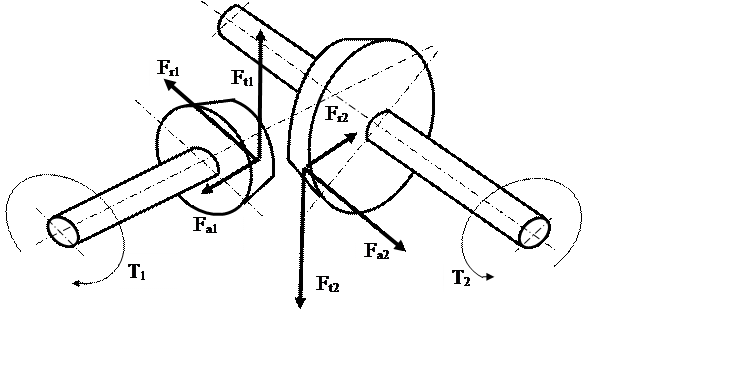Рисунок 2 - Силы, действующие в коническом зацеплении

5  Пример проектировочного расчета открытой конической зубчатой передачи

5.1 Исходные данные

Мощность Р₁  на валу шестерни, кВт -3,26.

Мощность Р₂  на валу колеса, кВт - 3,06.

Вращающий момент Т₁  на шестерне, Н·м -1112,2.

Вращающий момент Т₂  на колесе, Н·м - 2927,3.

Частота вращения  n₁  шестерни, мин^-1 - 28.

Частота вращения  n₂  колеса, мин^-1 - 10.

Передаточное число  - 2,8.

Срок службы передачи L_h , час - 24000.

Типовой режим нагружения передачи – II.

Передача нереверсивная.

В приводе используется асинхронный электродвигатель АИР112М4УЗ (= 5,5 кВт, n_эд = 1432 мин^-1, Т_max/T_ном = 2,2).

Требуемая мощность электродвигателя по кинематическому  расчету = 5,122 кВт.

5.2 Выбор материалов и определение допускаемых напряжений

5.2.1 Суммарное число циклов перемены напряжений

Для шестерни:      N_∑1 = 60 · L_h · n₁ = 60·24000·28=40,32·10⁶.

Для колеса:           N_∑2 = 60 · L_h · n₂ = 60·24000·10=14,4·10⁶.

5.2.2 Эквивалентное число циклов перемены напряжений при расчете на изгибную выносливость

Для шестерни:        N_FE1 = μ_FE  · N_∑1 = 0,14·40,32·10⁶ = 5,645·10⁶, где μ_FE = 0,14 - коэффициенты приведения для типового   режима II     (см.таблицу 3).