Исследование устойчивости систем автоматического регулирования с использованием критерия Найквиста

Федеральное агентство по образованию

Национальный исследовательский университет

ресурсоэффективных технологий

Томский Политехнический университет

Отчет по лабораторной работе №4

по дисциплине «Основы теории управления»

Выполнил:

Студент группы 8В72

____Е.А. Тартаковский

Преподаватель:

______Коновалов В.И.

Томск 2010

            Цель работы:

            Исследование устойчивости систем автоматического регулирования с использованием критерия Найквиста.

            Ход работы:

            1. Построить модель системы:

Объект регулирование представляет собой последовательное соединение апериодического звена 1-го порядка и колебательного звена. Параметры звеньев: T1=0.5; K1=2; T=0.5; K=1; v=0.5;

Передаточная функция апериодического звена 1-го порядка: K/(Ts+1).

Передаточная функция колебательного звена: K/(T²s²+2Tvs+1).

Построим модель системы:

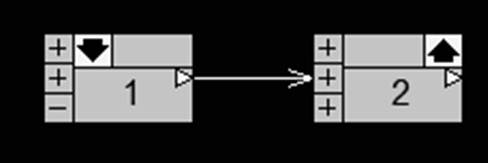
Рис. 1. Модель системы в Classic 3.01

            Здесь:

                        Блок 1 – апериодическое звено 1-го порядка;

                        Блок 2 – колебательное звено.

            Передаточные функции блоков:

                        1: 2/(0.5s + 1);

                        2: 1/(0.25s² + 0.5s + 1).

            2. Получить АФЧХ разомкнутой системы:

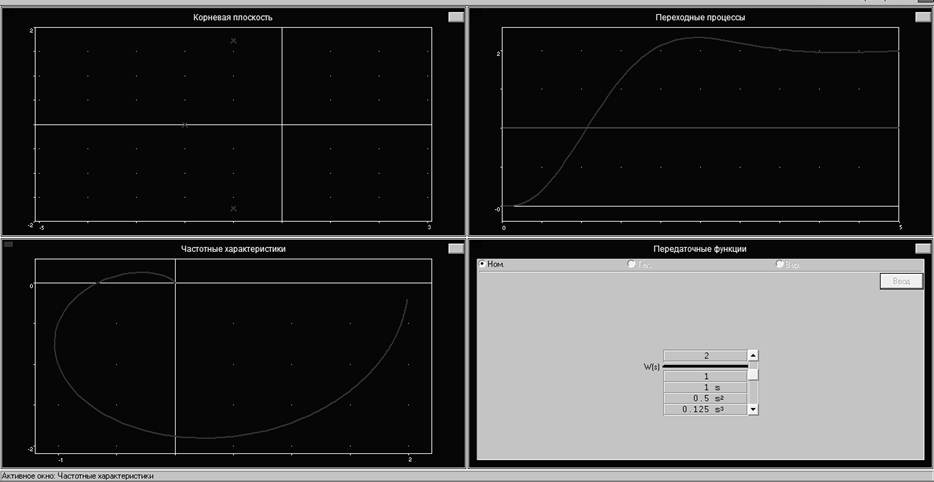
Рис. 2. Характеристики разомкнутой системы

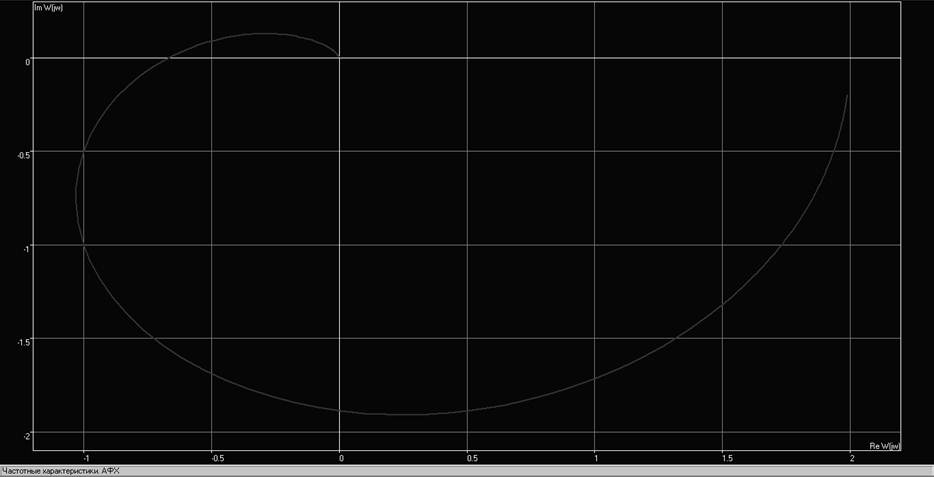
Рис. 3. Годограф разомкнутой системы

            По корневой плоскости видно, что характеристическое уравнение системы не имеет правых действительных корней, что означает, что система устойчива. График переходных процессов подтверждает это. Годограф Михайлова также соответствует годографу устойчивой системы.

            Следовательно, для определения устойчивости замкнутой системы следует воспользоваться первой формулировкой критерия Найквиста:

            Известно, что в разомкнутом состоянии система устойчива. Для устойчивости замкнутой системы требуется, чтобы АФЧХ разомкнутой системы при изменении w от нуля до бесконечности не охватывала точку с координатами (-1, i0).

            Увеличим масштаб:

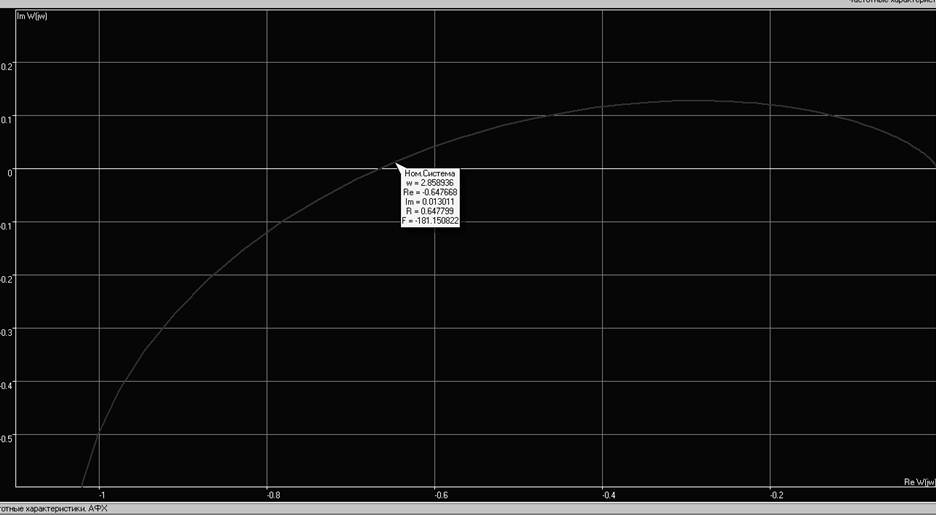
Рис. 4. Годограф разомкнутой системы в увеличенном масштабе

            Отсюда видно, что годограф разомкнутой системы пересекает действительную ось приблизительно в точке (-0.65, i0), и, соответственно, не охватывает точку (-1, i0). Из этого следует, что замкнутая система будет устойчивой.

            Замкнем систему и проверим полученный результат:

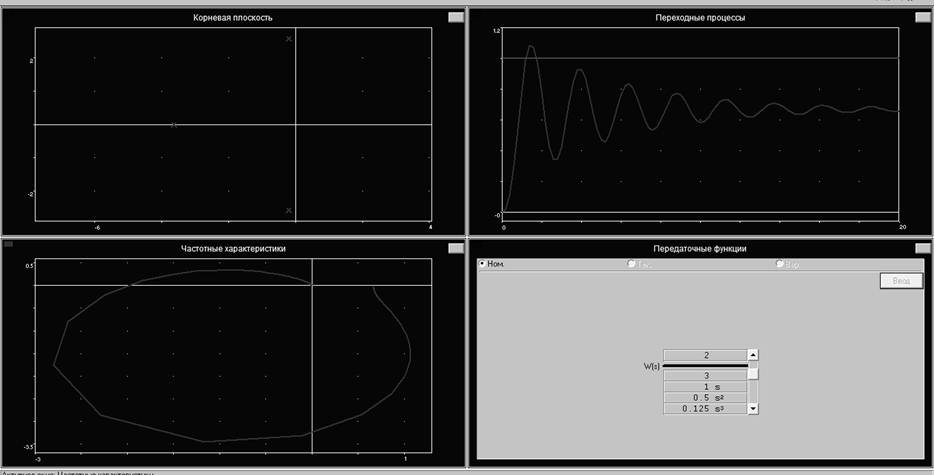
Рис. 5. Характеристики замкнутой системы

            По корневой плоскости видно, что характеристическое уравнение системы не имеет правых действительных корней, что означает, что система устойчива. График переходных процессов подтверждает это. Годограф Михайлова также соответствует годографу устойчивой системы.

            Таким образом подтвержден вывод об устойчивости замкнутой системы по критерию Найквиста.

            3. Исследовать экспериментально влияние коэффициента усиления разомкнутой системы на устойчивость замкнутой. Определить критическое значение коэффициента усиления:

Изначально К=1. Увеличивая К и наблюдая годограф системы, найдем такой К, при котором годограф пересекает действительную ось в точке (-1, i0).

            Приведем годографы промежуточного и найденного критического значений К.

            1 < K < Kкрит, K=1.25:

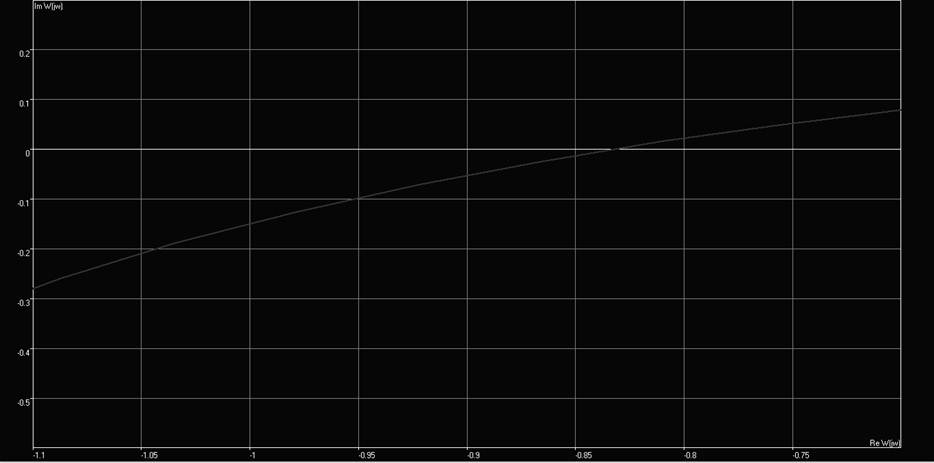
Рис. 6. Промежуточное значение коэффициента усиления

            Из графика видно, что при увеличении K точка пересечения годографом действительной оси приближается к критической.

            K=Kкрит=1.499:

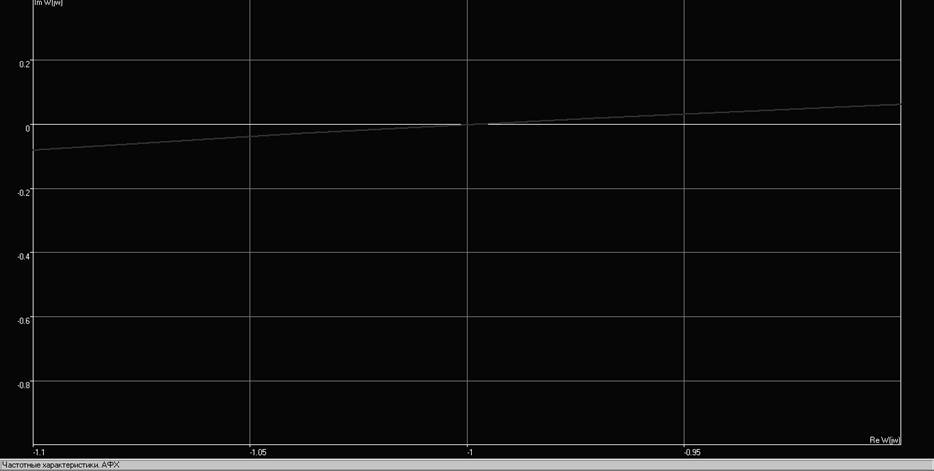
Рис. 7. Критическое значение коэффициента усиления

            При критическом K годограф пересекает действительную ось в точке (-1, i0).

            Получим годограф замкнутой системы для критического К:

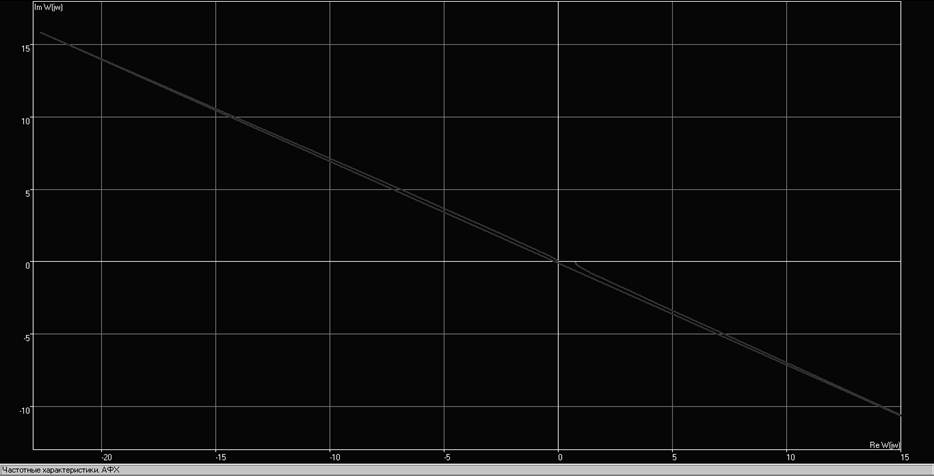
Рис. 8. Годограф замкнутой системы при К=Ккрит=1.499

            Увеличим масштаб:

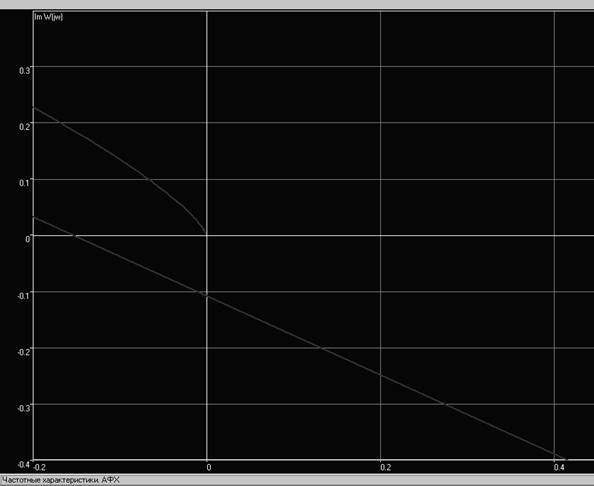
Рис. 9. Годограф замкнутой системы при К=Ккрит в увеличенном масштабе

            При критическом К=1.499 система все еще устойчива, что подтверждается по критерию Михайлова.

            Установим К=1.5, получим годограф замкнутой системы:

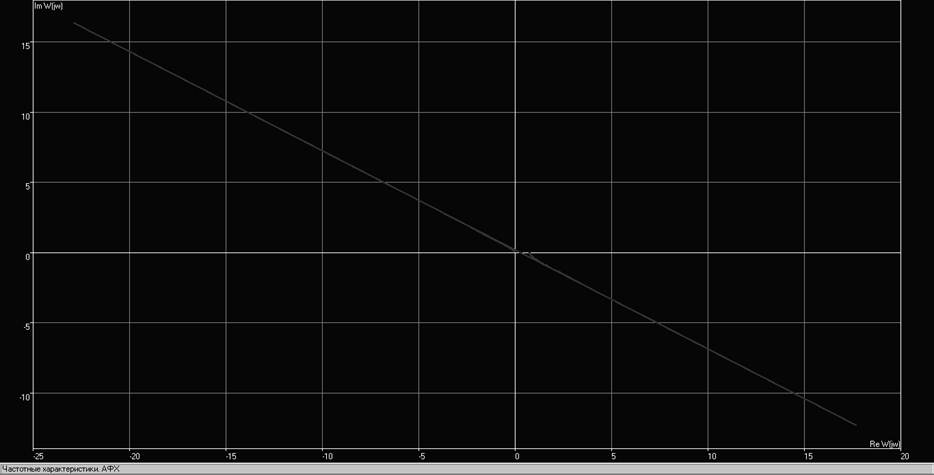
Рис. 10. Годограф замкнутой системы при К>Ккрит

            Увеличим масштаб:

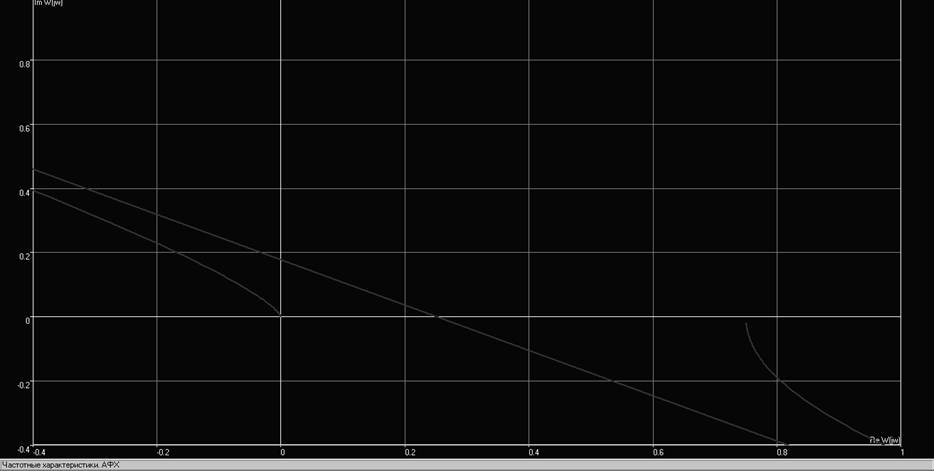
Рис. 11. Годограф замкнутой системы при К>Ккрит в увеличенном масштабе

            Как видно из годографа, система действительно неустойчива по критерию Михайлова.

            Рассчитаем теоретическое значение критического коэффициента усиления по критерию Гурвица, введя параметр критического коэффициента усиления Crit:

            Таким образом, получен теоретически рассчитанный по критерию Гурвица критический коэффициент усиления системы. Он совпадает с полученным практически коэффициентом.

            Установим К=0.5 Ккрит = 0.75 и определим запас устойчивости системы:

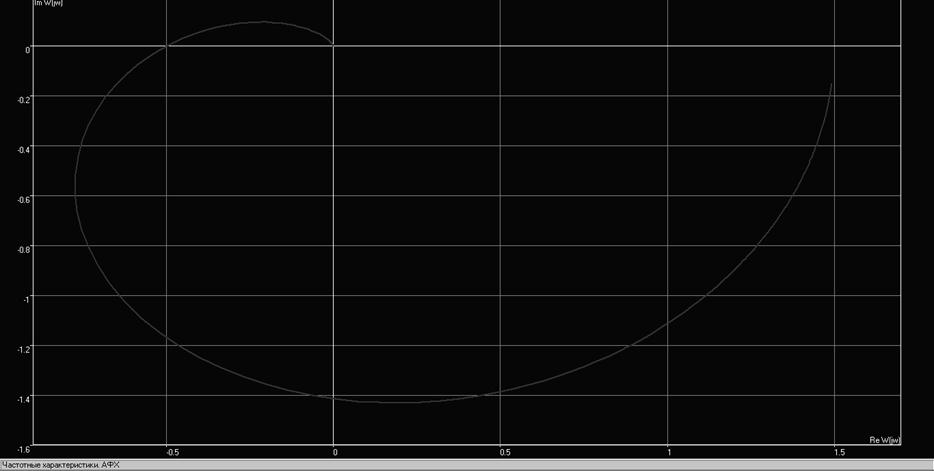
Рис. 12. Годограф разомкнутой системы при К=0.5 Ккрит

            Отсюда запас устойчивости по модулю = 0.5.

            Выводы:

            Во время выполнения работы выполнено исследование устойчивости САР с использованием критерия Найквиста, изучены различные формулировки этого критерия и получен навык определения устойчивости замкнутой системы по разомкнутой. Также был выполнен теоретический расчет критического для системы коэффициента усиления в соответствии с критерием Гурвица.