Исследование устойчивости систем автоматического регулирования с использованием критерия Михайлова

Федеральное агентство по образованию

Национальный исследовательский университет

ресурсоэффективных технологий

Томский Политехнический университет

Отчет по лабораторной работе №3

по дисциплине «Основы теории управления»

Выполнил:

Студент группы 8В72

____Е.А. Тартаковский

Преподаватель:

______Коновалов В.И.

Томск 2010

            Цель работы:

            Исследование устойчивости систем автоматического регулирования с использованием критерия Михайлова.

            Ход работы:

            1 Построение модели системы:

            Объект регулирование представляет собой последовательное соединение 2-х апериодических звеньев 1-го порядка и интегрирующего звена. Параметры звеньев: T1=0.34; K1=1.68; T2=0.43; K2=4.88; K3=5.76.

Передаточная функция апериодического звена 1-го порядка: K/(Ts+1).

Передаточная функция интегрирующего звена: K/s.

Построим модель системы:

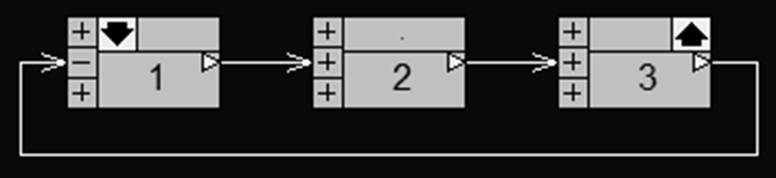
Рис. 1. Модель системы в Classic 3.01

            Здесь:

                        Блоки 1 и 2 – апериодические звенья первого порядка;

                        Блок 3 – интегрирующее звено.

            Передаточные функции блоков:

                        1: 1.68/(0.34s + 1);

                        2: 4.88/(0.43s + 1);

                        3: 5.76/s.

            2 Получим характеристики системы при замкнутой отрицательной обратной связи:

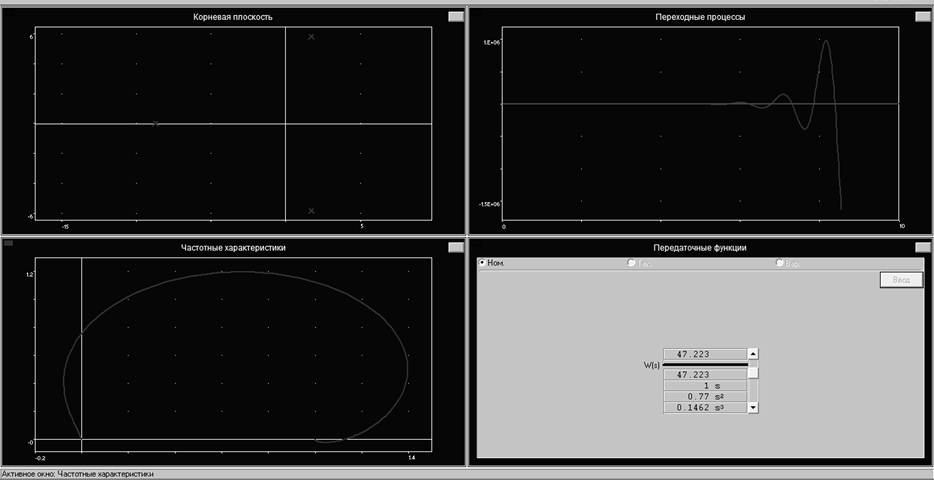
Рис. 2. Характеристики системы при замкнутой отрицательной обратной связи

            По корневой плоскости видно, что характеристическое уравнение системы имеет правые действительные корни, что означает, что система неустойчива. График переходных процессов подтверждает это. Годограф Михайлова также не соответствует годографу устойчивой системы.

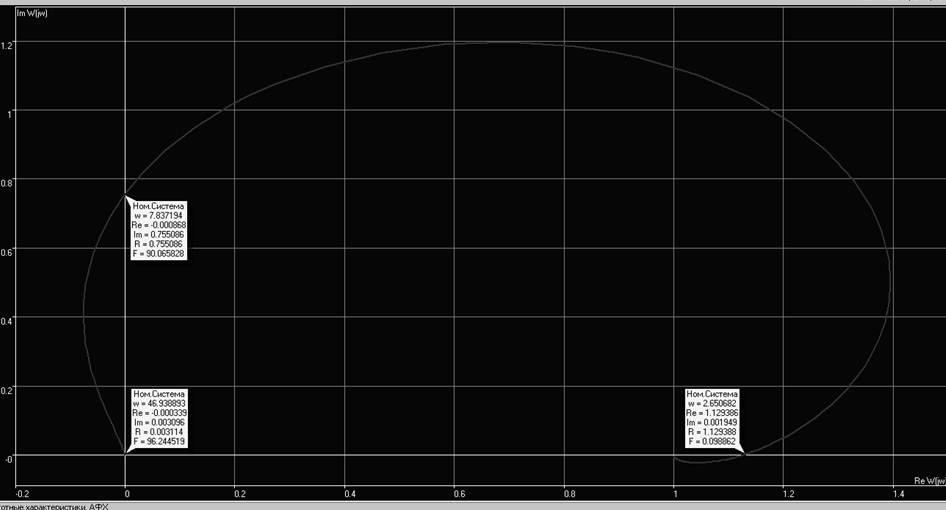
Рис. 3. Годограф неустойчивой системы с указанием частот в точках пересечения с осями координат

            Составим модель вспомогательной устойчивой системы и постоим ее годограф:

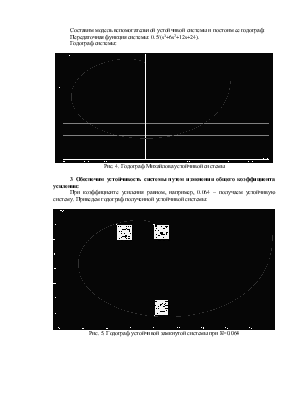
            Передаточная функция системы: 0.5/(s³+6s²+12s+24).

            Годограф системы:

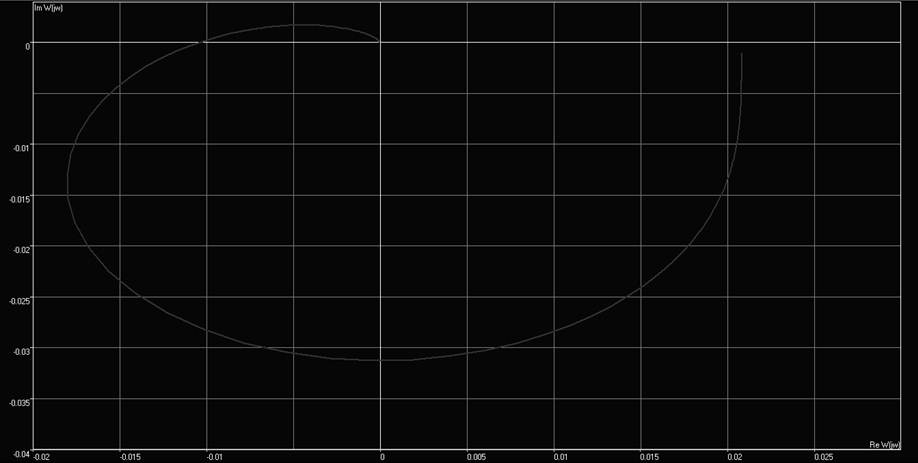
Рис. 4. Годограф Михайлова устойчивой системы

            3 Обеспечим устойчивость системы путем изменения общего коэффициента усиления:

            При коэффициенте усиления равном, например, 0.064 – получаем устойчивую систему. Приведем годограф полученной устойчивой системы:

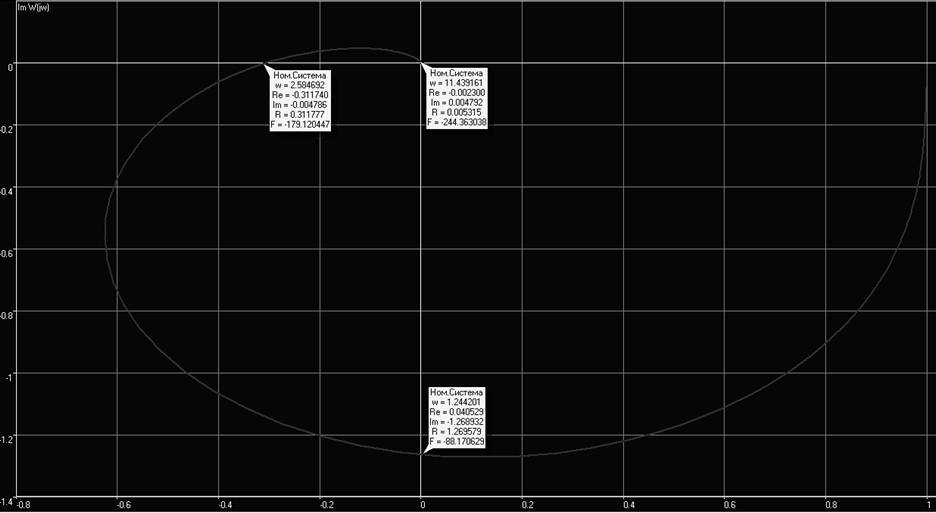
Рис. 5. Годограф устойчивой замкнутой системы при К=0.064

            4 Обеспечим устойчивость системы введением местной обратной связи от второго апериодического звена к первому:

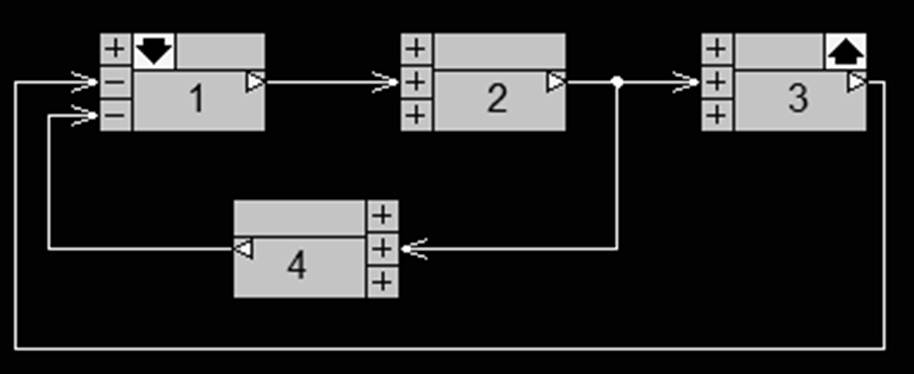
Рис. 6. Модель системы в Classic 3.01 с введенной местной отрицательной обратной связью от второго апериодического звена к первому

            Здесь 4 блок – дифференцирующее звено с передаточной функцией Ts. При T=1.5 система устойчива:

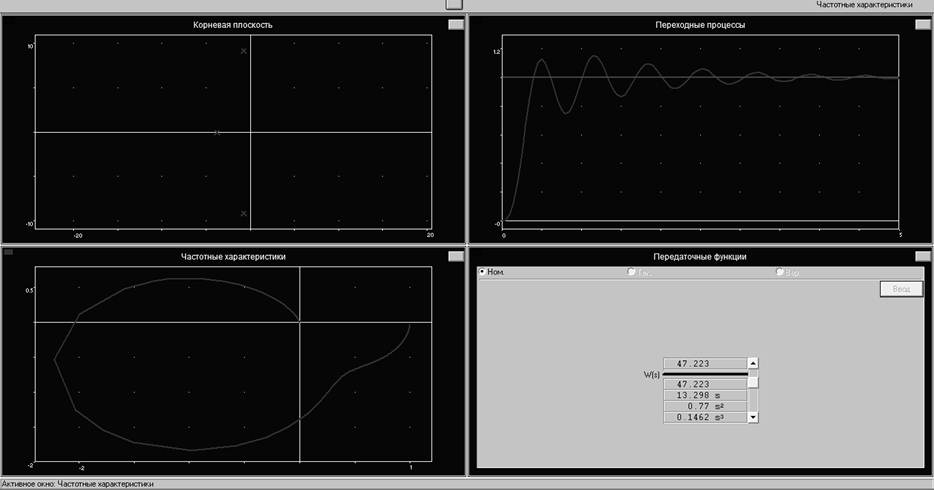
Рис. 7. Характеристики устойчивой системы с местной отрицательной обратной связью

            Укажем частоты в точках пересечения годографом осей координат:

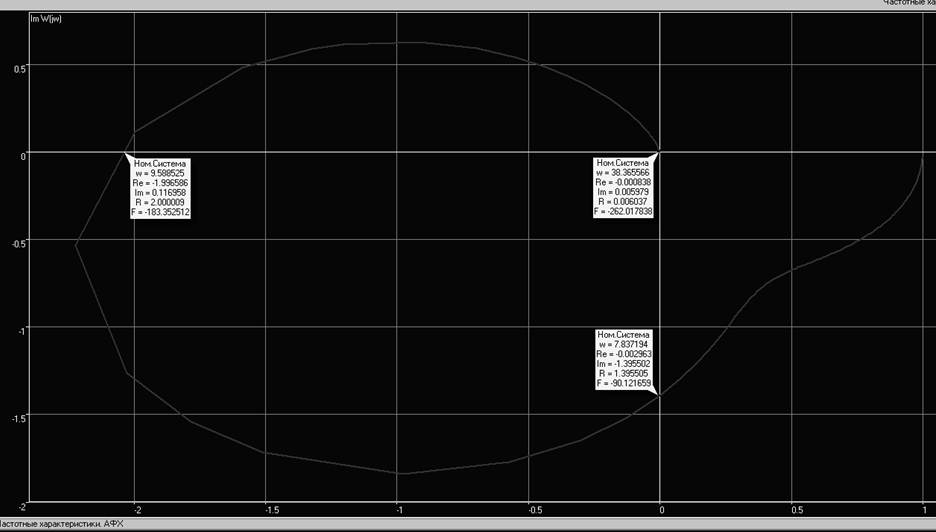
Рис. 8. Частоты в точках пересечения осей координат годографом

            Выводы:

Во время выполнения работы было выполнено исследование устойчивости САР по критерию Михайлова, обеспечена устойчивость САР путем изменения коэффициента усиления системы, а также путем ввода местной отрицательной обратной связи. Во время изучен критерий устойчивости Михайлова и получены годографы устойчивых и неустойчивых систем.