Векторы электромагнитного поля и параметры среды. Уравнения Максвелла в дифференциальной форме, страница 5

На рис. 3 приведен пример решения уравнения

для мкм;  При этом

 и рассматриваемое уравнение принимает вид

Рис. 3

.

Построив графики левой и правой частей уравнения, видим, что существуют две точки пересечения, т.е. условие одноволновости (одномодовости) не обеспечивается. Для обеспечения этого условия возьмем наибольшее значение R, при котором существует только одна точка пересечения. Таким значением оказывается R=3,2. Теперь, вычислив новое значение толщины световода h (h=2,42 мкм), построим новую окружность, соответствующую этому значению (штриховая линия на графике), и определим значение переменной t, соответствующее новой точке пересечения.

3. Если уравнение (12) имеет только одно решение (только одну точку пересечения уравнения окружности с графиком левой части), то в световоде существует одноволновый (одномодовый) режим работы. Если же существует несколько решений уравнения (12) , то условие одноволновости не выполняется и его выполнения нужно добиться подбором толщины световода h в формуле (13). Найденное таким образом значение толщины световода h используется во всех дальнейших расчетах.

4. Из решения трансцендентного уравнения (12) находим значение поперечного волнового числа g_^ в световоде. Поперечное же волновое число a_^ в окружающей световод среде найдем по формуле (10), постоянную распространения b из равенства

 , а фазовую скорость v_ф из соотношения

.

В условии задачи задается величина  или - мощность волны низшего типа, проходящей через поперечное сечение единичной ширины по оси Y либо среды 1, либо среды 2 соответственно.

Эту же величину можно определить по формуле

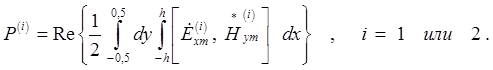        (14)

Подставляя в формулу (14) заданную величину или  и найденные в п.1 выражения для поперечных составляющих векторов электрического и магнитного полей, вычисляя интеграл и беря вещественную часть получившегося выражения, получим уравнение, из которого можно определить одну из двух постоян0ных А или В. Другую постоянную определим из граничных условий (11).

5. График зависимости каждой составляющей векторов напряженности электрического и магнитного полей для обеих сред строить в одной системе координат (для единой оси Х).

При построении зависимости амплитуд составляющих поля от координаты х должны быть указаны размерности всех величин, откладываемых по координатным осям!

6. Для определения процентного соотношения мощностей  и , проходящих через поперечное сечение сред 1 и 2, для низшего типа волны, следует по формуле (14) вычислить часть мощности, не указанную в условиях задачи, получив тем самым возможность определить суммарную мощность Р. Процентное соотношение определится из равенств:

         и           .

7. В этом пункте задания требуется, заменив плоский световод волоконным диаметром 2h, с параметрами e_r1 , m_r1 , окруженным защитной оболочкой с параметрами e_r2 , m_r2 , определить, обеспечивается ли при заланных параметрах и частоте f одноволновый (одномодовый) режим работы световода на волне основного (низшего) типа НЕ₁₁ , для которой .

Критические длины волн типов Н₀₁ и Е₀₁ , ближайших к основному типу рассчитываются по формуле (7). Одноволновый режим в сетоводе существует при

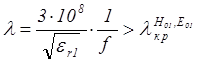 .                                         (15)

Если неравенство (15) не выполняется, то добиться одноволнового режима можно подбором значения относительной диэлектрической проницаемости e_r2 (так требуется в задании). Одноволновый режим будет существовать при всех e_r2 , удовлетворяющих неравенству

.

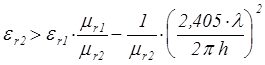Приложения.

1. Разложение ротора вектора по единичным векторам ортогональных систем координат:

- прямоугольная система координат x, y, z

 ;

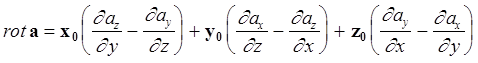- цилиндрическая система координат r, j, z

.

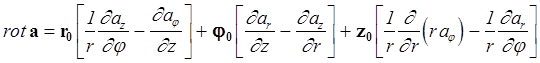2. Некоторые соотношения из теории функций Бесселя:

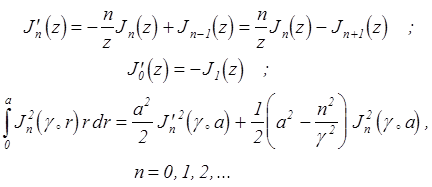
где - производная функции  по всему аргументу.