Векторы электромагнитного поля и параметры среды. Уравнения Максвелла в дифференциальной форме, страница 3

 , где

.

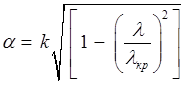В этом случае понятие длины волны в волноводе (L) теряет смысл и при построении графиков составляющих z следует брать от 0 до величины, обеспечивающей графическую точность рассматриваемой составляющей.

При построении зависимости составляющих векторов поля от координаты z для всех величин, откладываемых по координатным осям, должны быть указаны размерности!

4. Выполнение граничных условий на стенках направляющей системы можно проводить либо для комплексных амплитуд, либо для мгновенных значений составляющих векторов напряженности электрического и магнитного полей.

Проверяются на равенство нулю касательные к стенке волновода составляющие вектора  или нормальные составляющие вектора .

5. Определение плотностей составляющих поверхностного тока для прямоугольного и круглого волноводов производится по формуле

 

Для определения максимальных значений токов следует взять модули получившихся выражений.

Для коаксиального волновода напряжение между проводниками линии, токи, текущие по поверхности проводников и волновое сопротивление определяются по формулам

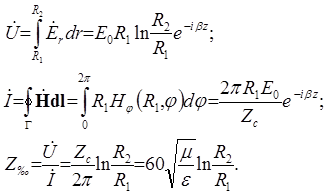
6. Средний за период поток энергии, переносимый через поперечное сечение волновода вычисляется по формуле

,                                                 (6)

где - функция комплексно-сопряженная с , а S_^ - площадь поперечного сечения волновода.

Таким образом, формула (6) принимает вид:

- для прямоугольного волновода

;

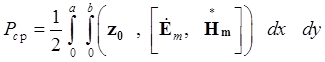- для круглого волновода

 ;

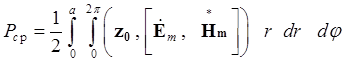- для коаксиального волновода

.

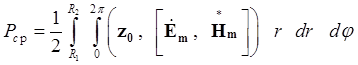Получающийся в случае круглого волновода интеграл от функции Бесселя вычисляется по формуле, приведенной в Приложении.

7. Фазовая скорость и скорость распространения энергии определяются по формулам

          и          .

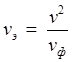8. Структуру векторных линий полей в волноводе следует строить в трех взаимно перпендикулярных сечениях прямоугольного волновода или в двух сечениях круглого волновода и коаксиальной линии, причем в продольном сечении (вдоль оси Z ) должны размещаться две длины волны.

Структуру токов в прямоугольном волноводе отображать, как если бы волновод был прозрачным.

ЗАДАНИЕ  НА  ВТОРУЮ  ЧАСТЬ  КУРСОВОЙ  РАБОТЫ

Во второй части курсовой работы, называемой “Электромагнитные волны в световодах” рассматривается плоский световод с диэлектрической проницаемостью(e₁), помещенный в неограниченную среду с диэлектрической проницаемостью (e₂). Поперечное сечение световода показано на рис. 2.

Остальные параметры световода и окружающей его среды определяются равенствами: m_r1=m_r2=1; s₁=s₂=0. Кроме того, задаются: частота ( f ) электромагнитных колебаний, толщина световода (2h) и мощность волны низшего типа (P⁽¹⁾ или P⁽²⁾),, проходящей через поперечное сечение единичной ширины по оси Y либо в первой, либо во второй среде соответственно.

Электромагнитная волна в первой и второй среде задается либо выражениями для комплексных амплитуд y-ой составляющей вектора напряженности электрического или магнитного поля (при равенстве нулю остальных составляющих этого вектора), либо значениями комплексных амплитуд одной из продольных составляющих векторов напряженности электрического или магнитного поля (при равенстве нулю продольной составляющей другого вектора). Амплитуды, задаваемых составляющих неизвестны и подлежат определению.

В процессе выполнения работы требуется: