Векторы электромагнитного поля и параметры среды. Уравнения Максвелла в дифференциальной форме, страница 2

6. Вычислить средний за период поток энергии через поперечное сечение волновода.

7. Определить фазовую скорость и скорость распространения энергии волны. Рассчитать и построить графики зависимостей этих скоростей от частоты.

8. Нарисовать структуру волновых линий и токов на стенках волновода.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ

ПЕРВОЙ ЧАСТИ КУРСОВОЙ РАБОТЫ

1. По способу задания поля все задачи делятся на два класса:

а) задается комплексная амплитуда вектора напряженности электрического или магнитного поля, имеющего только поперечную составляющую;

б) задаются комплексные амплитуды продольных составляющих векторов напряженности электрического и магнитного поля.

В первом случае комплексная амплитуда недостающего вектора электромагнитнгого поля находится по формуле

                                                          (1)

или

 .                                                       (2)

Формулы для вычисления дифференциального оператора  rotа в декартовой и цилиндрической системе координат приведены в Приложении. В выражениях (1) и (2) e_а и m_а  - абсолютные диэлектрическая и магнитная проницаемости соответственно, а w - круговая частота, связанная с заданной частотой  f  соотношением w=2p f.

Так как зависимость поля в направляющей системе от продольной координаты z описывается множителем , то производная любой составляющей по этой координате записывается в виде

, где  - одна из составляющих электромагнитного поля; x и h  - поперечные координаты (x и y в декартовой системе координат,  r  и j  в цилиндрической системе координат).

Во втором случае для нахождения комплексных амплитуд поперечных составляющих векторов и  используют соотношения, выведенные в [1, разд. 13.3] и связывающие эти составляющие с комплексными амплитудами продольных составляющих  и . Эти соотношения имеют вид:

- в декартовой системе координат

  ;

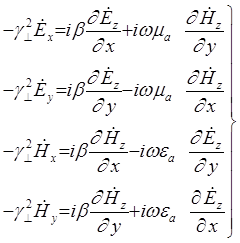- в цилиндрической системе координат

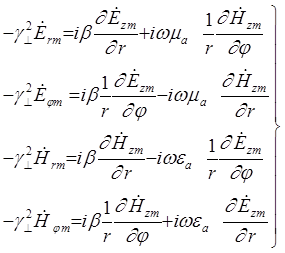, где

- поперечное волновое число, а b - коэффициент распространения волны вдоль направляющей системы.

2. Методика определения диапазона частот, в котором рассматриваемое поле представляет собой волну, бегущую вдоль оси Z, зависит от типа направляющей системы.

Для коаксиального волновода в условии задачи известна критическая длина волны типа Т (l_кр= ¥), поэтому критическая частота легко находится по формуле

 ,                                                                (3)

где

 - скорость света в среде, заполняющей волновод, и равна нулю.

Для круглого волновода задается значение корня функции Бесселя или ее производной (n), связанное с критической длиной волны равенством

 ,                                                               (4)

где  а - радиус волновода. Подставляя (9) в (7), найдем ¦_кр . Искомый диапазон определяется неравенством

 .                                                            (5)

Для прямоугольного волновода критическая длина волны либо задается неявно в формуле для коэффициента распространения b , например,

 

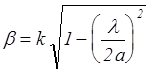
( l_кр=2а ), либо вычисляется по задаваемой формуле, например,

 

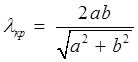
После определения l_кр , f_кр определяется по формуле (3), а искомый диапазон частот определяется неравенством (5).

3. Для получения выражений для мгновенных значений составляющих векторов напряженности электрического и магнитного полей необходимо взять действительную часть произведений соотношений для комплексных амплитуд на множитель .

При построении графиков зависимости мгновенных значений составляющих векторов напряженности электрического и магнитного полей следует обратить особое внимание на случай  f £ f_кр . В этом случае величина  оказывается меньше нуля и коэффициент распространения волны вдоль оси Z  (b ) оказывается мнимой величиной. Так как

, то, выбирая из физических соображений знак минус, получаем