Аналитического выражения для коэффициентов отражения и прохождения по давлению и по энергии. Аналитическое выражение для неоднородной волны

Санкт-Петербургский Государственный электротехнический университет им В.И. Ульянова (Ленина)

Кафедра ЭУТ

Курсовая работа

по курсу «Волновые задачи акустики»

Вариант 1.5

Выполнил:

Группа 0582

Преподаватель:

2014 г.

Содержание.

Задание………………………………………………………………………….3

Аналитического выражения для коэффициентов отражения и прохождения по давлению и по энергии……………………...4

Критический угол…………………………………………………………….13

Аналитическое выражение для неоднородной волны……………………..14

Численный анализ модулей и фаз коэффициентов отражения и прохождения по давлению и по энергии в диапазоне углов падения от 0 до 90……………………………………………………………19

Задание.

На бесконечную плоскую границу раздела двух сред 1 и 2, под углом θ, отсчитываемым от нормали к границе раздела, из среды 1 падает плоская гармоническая волна.

1.  Найти аналитическое выражение для коэффициентов отражения и прохождения по давлению и по энергии.

2.  Определить критический угол.

3.  Получить аналитическое выражение для неоднородной волны.

4.  Провести численный анализ модулей и фаз коэффициентов отражения и прохождения по давлению и по энергии в диапазоне углов падения от 0^о до 90^о.

Результаты численного анализа представить в графической форме. Номера вариантов и физические параметры рассматриваемых сред приведены в таблицах 1 и 2.

Таблица 1

№ варианта	5
Среда 1	Кремний–органическая жидкость
Среда 2	Вода

Таблица 2

Среда	С, м/с	ρ, кг/м3	ρС, кг/м2с (Па·с/м)
Кремний–органическая жидкость	1270	1000	1.27·106
Вода	1500	1000	1.5·106

Аналитического выражения для коэффициентов отражения и прохождения по давлению и по энергии.

Рассматриваемые среды будем считать лишенными вязкости, поэтому в них могут распространяться только продольные волны. Для жидких сред акустические задачи решаются проще с использованием такой вспомогательной абстрактной величины, как скалярный потенциал колебательной скорости φ. С физическими величинами (колебательной скоростью ξ, давлением p, смещением ξ) он связан простыми соотношениями:

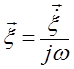 ,         ,        .                                                 (1)            

Для описания волн воспользуемся частным решением волнового уравнения в прямоугольной системе координат

,   (2)

где    ;     ;     -орты вдоль координатных осей. Пусть из среды І со скоростью звука  и плотностью , занимающей верхнее полупространство z>0, на границу раздела z=0  со средой ІІ с параметрами , , занимающей нижнее полупространство z<0, падает монохроматическая плоская волна частоты  (рис.1). Границу считаем неподвижной, поэтому частоты всех волн одинаковы. Плоскость xz совместим с плоскостью падения. При этом волновые векторы всех волн окажутся в плоскости xz  и не будет иметь проекций на ось y  .

С учетом (2) опишем поля падающей , отраженной  и преломленной  волн:

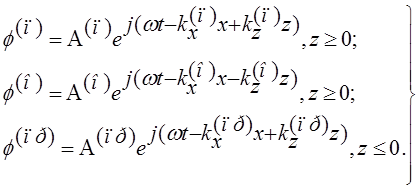                                                         (3)               

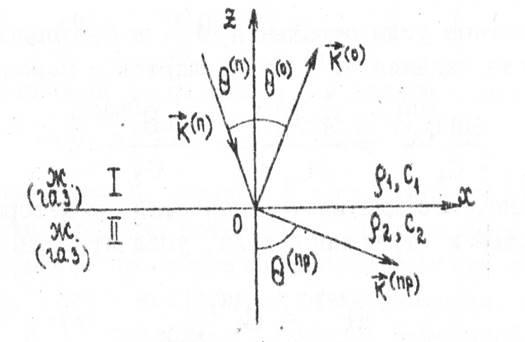
рис.1

Введем упрощающие запись обозначения для волновых чисел падающей, отраженной и преломленной волн:

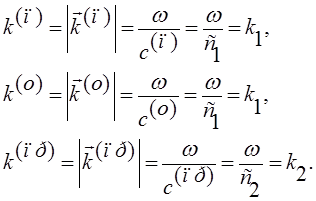
Здесь , так как волны (и падающая, и отраженная) распространяются в среде І. Выразим проекции волновых векторов через углы падения , отражения и преломления :

 

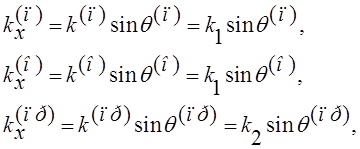
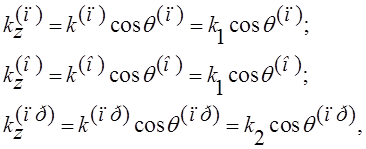
тогда (3) перепишутся в виде

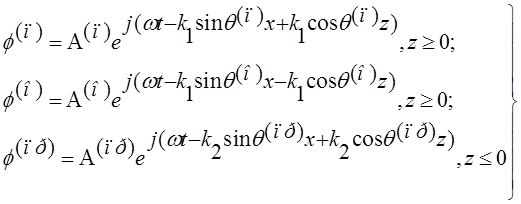                                        (4)                                                              

Неизвестные углы отражения и преломления при заданном угле падения определяются с помощью закона Снеллиуса:

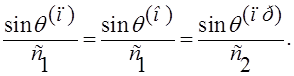                                                                              (5)                                        

Из него видно, что для изотропных сред, у которых равны скорости падающей и отраженной волн, угол отражения равен углу падения

                                                                                                         (6)    

Для нахождения неизвестных амплитуд отраженной и преломленной волн воспользуемся граничными условиями: непрерывностью нормальной компоненты вектора колебательной скорости

                                                                                                   (7)

и непрерывностью давления

                                                                                               (8)