Аналитического выражения для коэффициентов отражения и прохождения по давлению и по энергии. Аналитическое выражение для неоднородной волны, страница 2

Используя выражения (1),

     

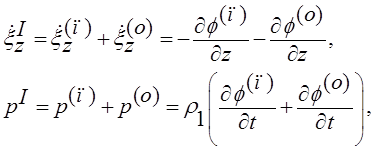
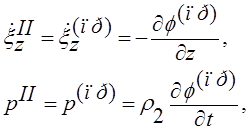
То (7) и (8) примут вид:

                                                                                                                                                                                                                         

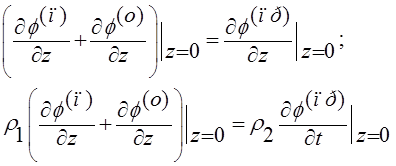
Подставим (4) в (9) и (10), сократим на экспоненциальные множители, учитывая (6), получим систему неоднородных алгебраических уравнений:

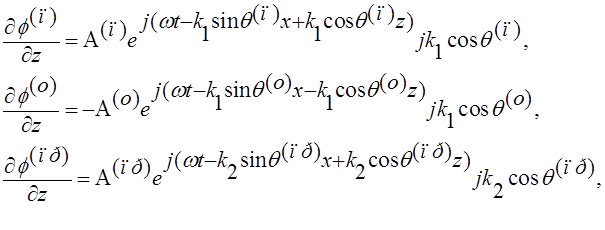
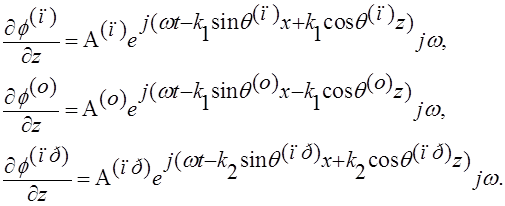
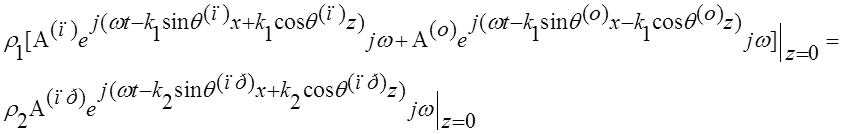
в итоге получили

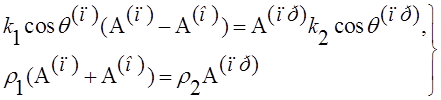                                                   (11)                            

Разделим оба уравнения на  введем обозначения

  ,                                   

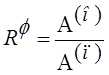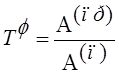
Назовем  коэффициентом отражения по потенциалу, а - коэффициентом  прохождения по потенциалу. В литературе  называют также коэффициентом  прозрачности границы или коэффициентом прозрачности границы или коэффициентом пропускания, реже коэффициентом преломления. Введение коэффициентов  и позволяет проводить относительную оценку амплитуд волн, участвующих в процессе отражения- преломления, и исключить задание амплитуды падающей волны. Система уравнений (11)примет вид:

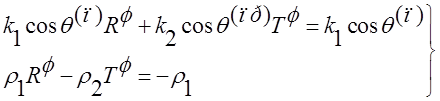
Решаем её относительно неизвестных   и  :

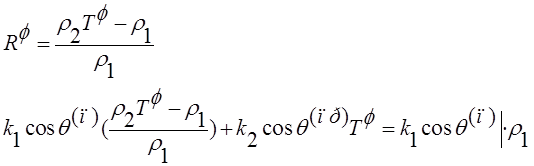
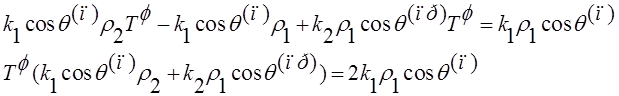
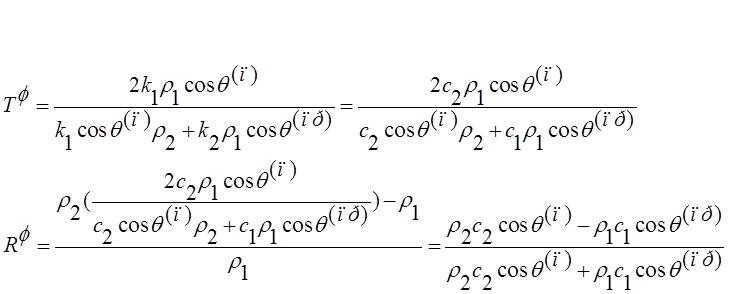
в итоге получили

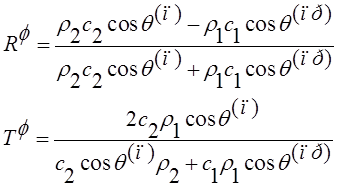
(12)

В акустических расчетах часто применяют выражение для коэффициентов отражения и прохождения других полей. Выразим их через уже полученные и .

Коэффициенты отражения и прохождения по давлению.

Представим давление через потенциал колебательной скорости

где - комплексная амплитуда давления. Коэффициент отражения по давлению будет:

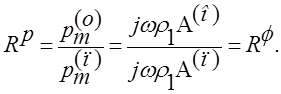                                                                             (13)                                         

Для коэффициента прохождения  по давлению получим:

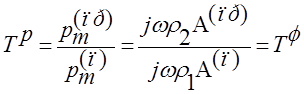                                                                         (14)                                                           

Коэффициенты отражения и прохождения по плотности потока энергии.

В акустических расчетах чаще всего используется комплексная форма записи величин.

Однако при вычислении энергетических характеристик используются только вещественные части комплексных величин, входящих в расчетные соотношения. Мгновенное значение вектора плотности потока энергии можно вычислить как

Представляет практический интерес среднее за период колебаний значение вектора плотности потока энергии

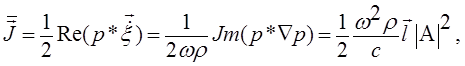                                              (15)                                         

где черта означает усреднение за период; звездочка - комплексное сопряжение; - амплитуда колебательной скорости.

Коэффициенты отражения и прохождения определим для проекции среднего за период  вектора плотности потока энергии на направление распространения  волны , т.е. для среднего за период значения интенсивности:

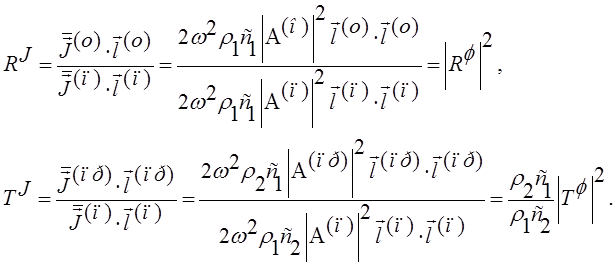
Коэффициенты отражения и прохождения по потоку энергии.

Поток энергии - это количество энергии, проходящее через плоскую площадку площадью S.

Среднее за период значение потока энергии можно представить как

где - единичная нормаль к площадке с площадью S.

Если волна распространяется перпендикулярно площадке, то  и можно написать

                                                                                                  (16)

Для получения коэффициентов отражения и прохождения рассмотрим энергетические трубки падающей, отраженной и преломленной волн с площадями сечений соответственно  (рис. 2). Эти сечения будем считать прямоугольными, причем ширина  всех сечений в направлении оси y будет одинакова, так как все энергетические трубки параллельны плоскости падения xz. С помощью рис.2. площади сечений можно представить

           

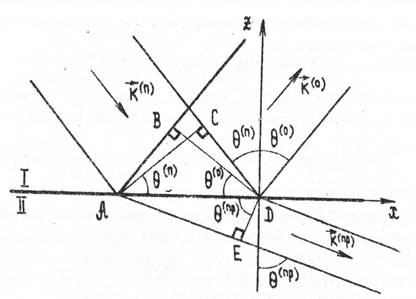
рис. 2

Выразив AC,BD и DE через длину общей области взаимодействия трубок AD, учитывая, что , получим:

     .

С учетом (16) коэффициенты отражения и прохождения будут иметь вид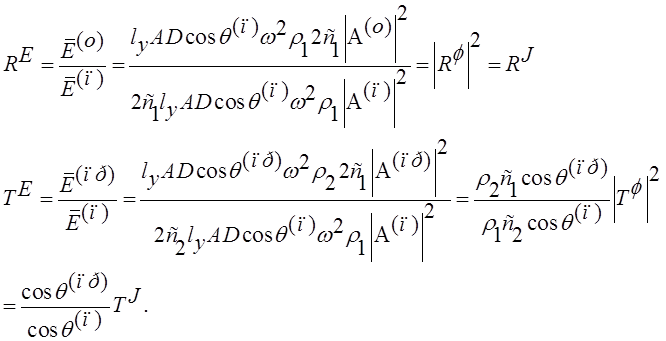                    

На основании закона сохранения энергии полученные коэффициенты связаны соотношением

Отметим, что полученную формулу (18) можно использовать только в случае, если в процессе отражения- преломления отсутствует явление полного внутреннего отражения, когда преломленная волна является неоднородной.

Критический угол.

Из закона Снеллиуса следует, что если >, то >. Это говорит о том, что при увеличении угла падения угол преломления достигает значения  раньше, чем угол падения. При этом преломленная волна начнет «скользить» вдоль границы раздела сред. Угол падения, при котором  и преломленная волна «скользит» вдоль границы, называется критическим углом:

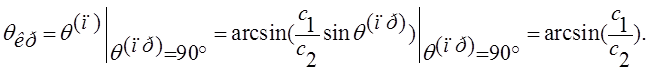
Аналитическое выражение для неоднородной волны.