











Курсовой проект
СИНТЕЗ ОПТИМАЛЬНОЙ СИСТЕМЫ УПРАВЛЕНИЯ
Цель работы – закрепление теоретических знаний по теории систем управления с помощью расчета оптимального регулятора и компьютерного моделирования системы управления.
Задача работы заключается в выборе структуры и параметров регулятора по интегральному квадратичному критерию.
1.ОБЪЕКТ УПРАВЛЕНИЯ
Объект управления задан в ![]() мерном пространстве
состояния векторным дифференциальным уравнением
мерном пространстве
состояния векторным дифференциальным уравнением
(1) ![]() , где векторы
, где векторы ![]() считаются
одностолбцовыми матрицами, квадратная постоянная матрица
считаются
одностолбцовыми матрицами, квадратная постоянная матрица ![]() имеет размер
имеет размер ![]() . Собственные
значения матрицы
. Собственные
значения матрицы ![]() произвольны.
произвольны.
Цель управления состоит в приведении системы к нулевому состоянию при минимизации интегрального квадратичного критерия:
(2) 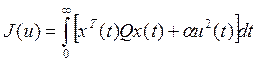 , где матрица
, где матрица![]() положительно
определенная, коэффициент
положительно
определенная, коэффициент ![]() .
.
Такого рода критерии часто используются для оценки качества длительной работы системы управления в режиме нормальной эксплуатации.
Выбор параметров критерия (2) можно связать с прямыми показателями качества.
2. ЗАДАНИЕ
Используя заданные для данного варианта параметры в (1) и (2) и пакеты прикладных программ рассчитать оптимальные параметры линейной обратной связи
(3)
![]() , т.е. коэффициенты
вектора
, т.е. коэффициенты
вектора ![]() . Провести
компьютерное моделирование оптимальной системы и получить графики элементов
вектора состояния. Выяснить влияние погрешностей решения и малых нелинейностей.
. Провести
компьютерное моделирование оптимальной системы и получить графики элементов
вектора состояния. Выяснить влияние погрешностей решения и малых нелинейностей.
3.ПОРЯДОК ВЫПОЛНЕНИЯ
1.Написать
характеристическое уравнение матрицы ![]() и
определить устойчивость однородной системы
и
определить устойчивость однородной системы ![]() по критерию Гурвица.
по критерию Гурвица.
Используя пакет СС вычислить собственные числа.
2.Проверить систему (1) на управляемость.
3.Составить алгебраическое матричное уравнение Риккати:
(4)
![]()
В пакете СС решить
линейно-квадратичную задачу и получить вектор ![]() для уравнения
обратной связи (3).
для уравнения
обратной связи (3).
4.Вычислить матрицу оптимальной системы
(5)
![]() .
.
и проверить её устойчивость по критерию Гурвица.
5.Смоделировать переходные процессы в оптимальной системе и вычислить критерий (2) в пакете TUTSIM. Получить графики процессов.
6.Исследовать
влияние неточности вычислений вектора ![]() на величину критерия
и качество процессов.
на величину критерия
и качество процессов.
7.С помощью датчика случайных чисел NOI исследовать влияние шума на переходные процессы.
8.Принять ![]() , где
, где ![]() , при
, при ![]() и
и ![]() при
при ![]() .
.
Исследовать
устойчивость по параметру ![]() с
помощью критерия Попова.
с
помощью критерия Попова.
Для этого построить в пакете СС частотную характеристику по передаточной функции.
4. ФОРМА И СОДЕРЖАНИЕ ОТЧЕТА
При защите курсового проекта студент должен продемонстрировать работающую программу, обеспечивающую
1) задание параметров;
2) моделирование динамических процессов ;
3) решение линейно-квадратичной задачи;
4) оценку изменений процессов при вариации параметров возмущений.
Пояснительная записка должна содержать
1)задание на проект;
2)краткие выдержки из теории управления;
3)систему уравнений модели;
4)блок-схему моделирования;
5)листинг структуры;
6) результаты моделирования в виде графиков;
7)сравнительный анализ результатов и выводы
Требуется получить графики временных зависимостей всех координат системы.
На защите курсовой работы студент должен показать уверенное владение техникой компьютерного моделирования, умение составлять и реализовывать схемы моделирования, знакомство с основами теории управления.
ПРИЛОЖЕНИЕ.
МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ НА ПЭВМ
ВО ВРЕМЕННОЙ ОБЛАСТИ
ПРЕДИСЛОВИЕ
Данные указания содержат описание входного языка пакета прикладных программ DYNSIM для моделирования на ПЭВМ непрерывных динамических систем и процессов.
Проблемно-ориентированный язык позволяет описывать математические модели, заданные в виде структурных схем, либо в виде систем обыкновенных дифференциальных и алгебраических уравнений, и является своего рода реализацией принципа аналогового моделирования на цифровой ЭВМ.
Программная система реализована на ПЭВМ типа IBM PC .
1. ЭЛЕМЕНТЫ ВХОДНОГО ЯЗЫКА
1.1 Общие замечания
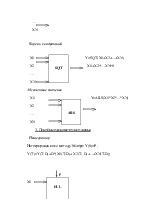
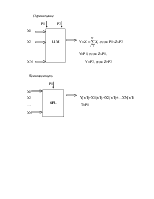
Рассматриваемая программная система (ПС) является диалоговой и использует проблемно-ориентированный язык (ПОЯ), реализующий принципы аналогового моделирования на цифровой ЭВМ. Моделируемая динамическая система представляется в виде схемы моделирования в терминах ПОЯ и описывается программой, включающей операторы структуры, параметров и управления. Основу ПОЯ составляют набор функциональных блоков (табл. 1.1).
Основными элементами входного языка являются числовые константы, символические имена, операторы, команды диалога.
Операторы структуры описывают связи переменных в схеме моделирования. Операторы параметров служат для присвоения числовых значений параметрам, константам, начальным условиям, таблично задаваемым переменным. Операторы управления служат для организации расчетов и вывода результатов.
При моделировании следует учитывать, что хотя формальное ограничение количества используемых при моделировании блоков отсутствует, на практике каждые дополнительные сто блоков ПОЯ требуют примерно 2К оперативной памяти ПЭВМ.
1.2 Числовые константы
Допускается применение числовых констант целого и вещественного типа. Правила их написания не отличаются от общепринятых:
24.576 Е08
-2.862 Е-8
-56.234
Общее число символов в записи вещественных констант не должно превышать двенадцати, абсолютная величина должна быть в пределах от 2.7Е-41 до 9.2Е38
1.3 Символические имена
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.