Синтез оптимальной системы управления. Закрепление теоретических знаний по теории систем управления с помощью расчета оптимального регулятора и компьютерного моделирования системы управления, страница 3

В дополнение к этому перечню можно использовать в процессе работы с ПС некоторые команды операционной системы MS DOS:

"CTRL/S"       - фиксирует кадр на экране дисплея. После ввода  любого символа (кроме пробела) вывод данных продолжается.

"CTRL/NumLock" – то же действие, что и при команде "CTRL/S"

"CTRL/C"       - возврат в MS DOS

"CTRL/BREAK"   - тоже действие, что и при команде "CTRL/C"

"|<-"          - удаление символа перед курсором.

"ESC"          - перемещение текущей строки символов.

"SHIFT/PRTSC"  - печать на принтере содержимого экрана дисплея.

"CTRL/PRTSC"   - подключение принтера в параллель к дисплею.

Символ  " / " означает одновременное нажатие двух указанных в  команде ключей.

2.  ПОСТРОЕНИЕ И ВВОД БЛОК-СХЕМЫ МОДЕЛИ

2.1 Построение и ввод блок-схемы модели на ПОЯ

Для введения в ПЭВМ информации о моделируемой системе необходимо построить блок-схему модели, представляющую собой  отображение модели в виде связанных и пронумерованных блоков ПОЯ из их ограниченного набора (табл. 1.1). Программа, соответствующая построенной  таким образом блок-схеме, состоит из четырёх сегментов:  структура  модели, параметры модели, выходные блоки, параметры таймера.

В общем случае функциональный блок ПОЯ имеет вид представленный на рис 2.1. Следует отметить что отдельные блоки имеют строго предписанное число входов и/или параметров.

Следует внимательно отнестись к выбору метода численного интегрирования. Возможности ПС включают использование двух  методов: Эйлера и Адамса-Башфорта.

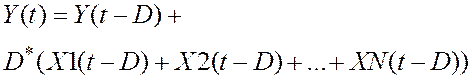                (2.1)

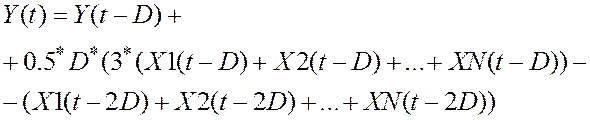(2.2)

Заметим, что при интегрировании гладких функций более точное решение получается с применением метода Адамса-Башфорта   (2.2).

Однако, при наличии разрывов в  функциях  или  резких изменениях предпочтительнее использовать метод Эйлера (2.1).

2. Элементарные математические функции                                            

Тригонометрические

SIN COS

              X1

             X2                                                                             Y=SIN(X1+X2+…+XN)

             …

             XN                                                                              Y=COS(X1+X2+…+XN)                        

EXP

   Экспонента

                      X1                                                                 Y= EXP(X1+X2+…+XN)                                            

                      X2                                                                                         

                      …

XN

Логарифм   натуральный

LOG

       X1

       X2                                                                                  Y=LN(X1+X2+...+XN)

       …

XN

Корень  квадратный

	SQT

 

    X1                                                                        Y=SQT(X1+X2+...+XN)                                                                                                                                                                                                                                    

    X2                                                                           X1+X2+…XN>0