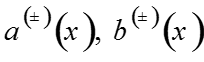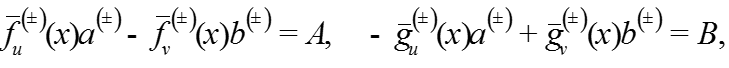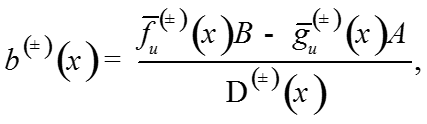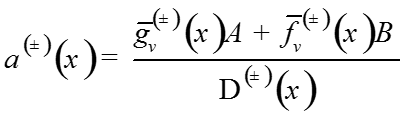КСТС для системы эллиптических уравнений

Физический факультет МГУ им. Ломоносова кафедра математики

КСТС для системы эллиптических уравнений

Научный руководитель:

Москва 23.05.2012

• Рассматривается краевая задача для системы двух уравнений второго порядка с разными степенями малого параметра
• (1)
• f и g – достаточно гладкие функции.

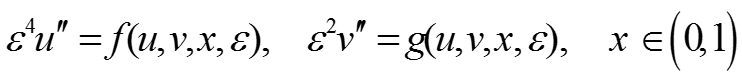
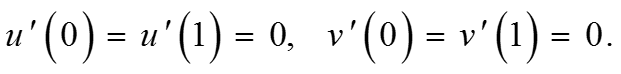
u v x g v1 v2 v3 v

• У1:
• У2:

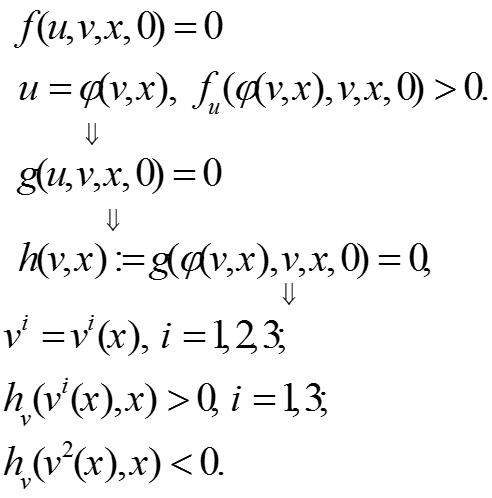
Обозначим У3: Пусть существует единственная точка - решение уравнения , причем .

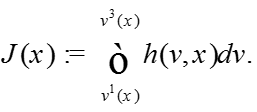
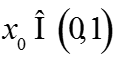
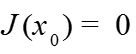
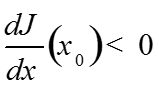
Условие квазимонотонности

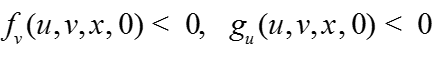
• Условие4: всюду в области

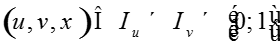
КСТС

Асимптотика

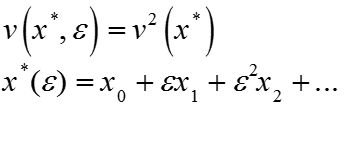
• Точка перехода:
• Асимптотика решения задачи строится отдельно справа и слева от точки перехода :
• где

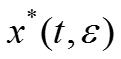
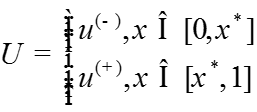
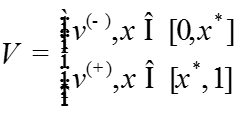
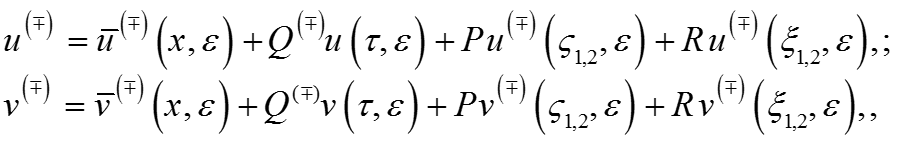
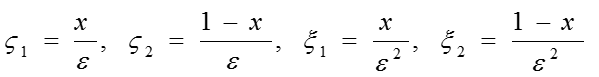
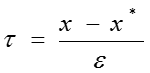
• Условия непрерывности асимптотического разложения v – компоненты решения в точке :
• Условия непрерывности производных асимптотических разложений в точке .

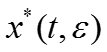
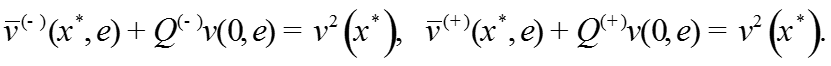
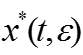
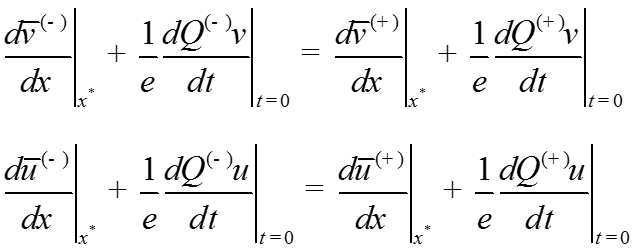
Регулярные члены асимптотики

• Для функций получается вырожденная система:
• Из условий У1 и У2 получаем:

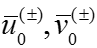
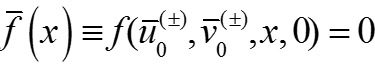
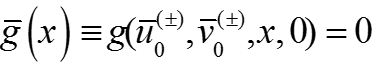
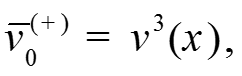
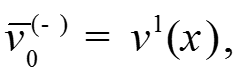
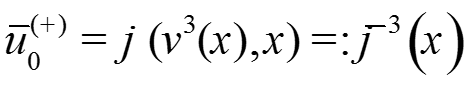
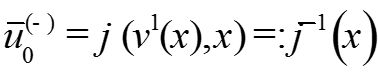
Система уравнений для функций переходного слоя

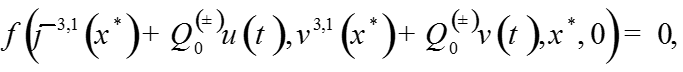
(1) где

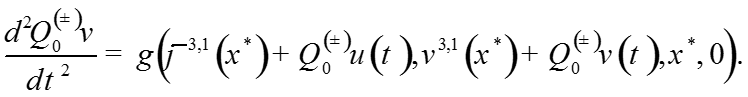
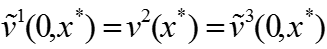
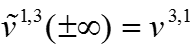
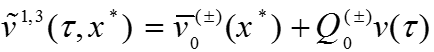
Обоснование асимптотики

• Теорема. При выполнении условий A1-A4 для достаточно малого существует решение задачи , для которого функции являются равномерным на [0;1] асимптотическим приближением с точностью порядка

• Функции имеют вид:

,

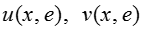
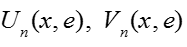
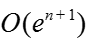
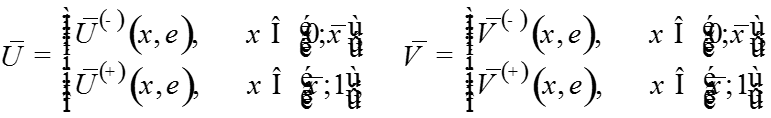
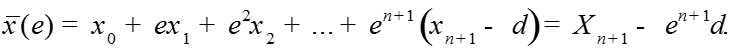
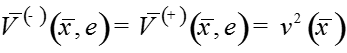
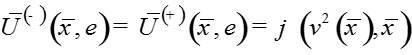
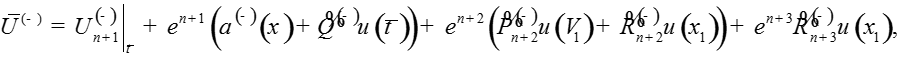
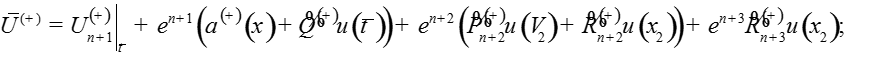
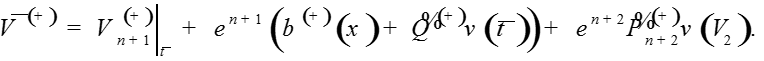
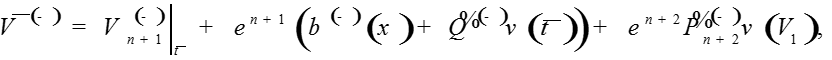
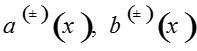
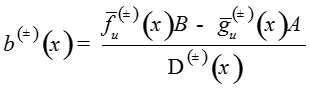
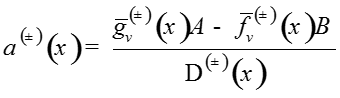
.ОБОСНОВАНИЕ АСИМПТОТИКИ В СЛУЧАЕ ОБРАТНОЙ КВАЗИМОНОТОННОСТИ

• Условие A4'. (Условие квазимонотонности).
• всюду в области .

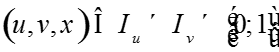
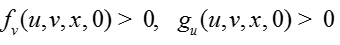
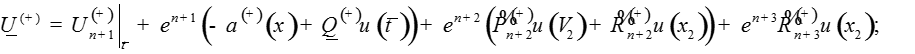
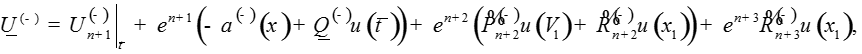
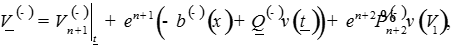
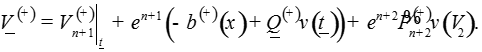
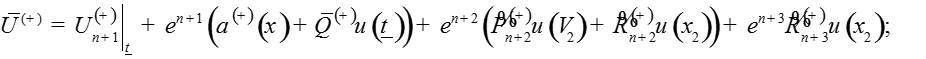
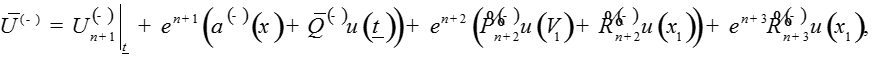
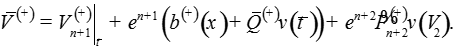
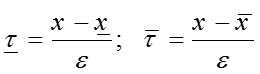
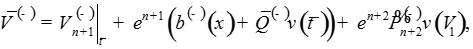
• Определим функции как решения систем
• уравнений
• где A и B – положительные числа.
• Запишем решение системы:
• где
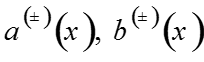
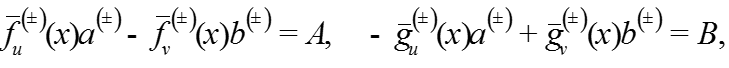
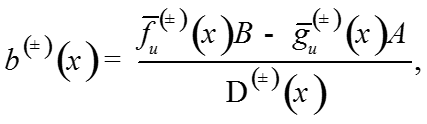
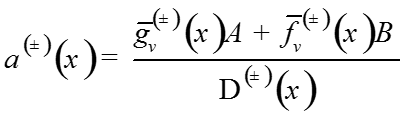
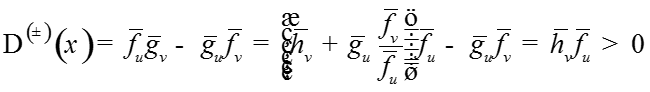
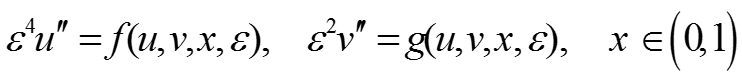
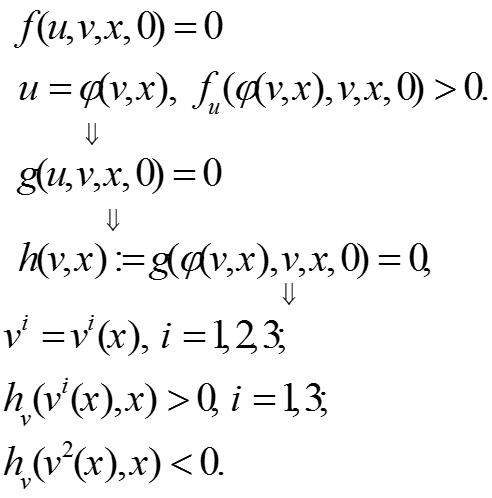
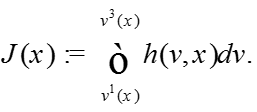
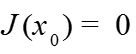
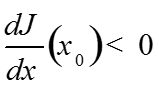
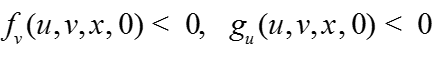
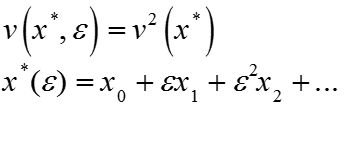
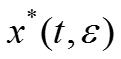
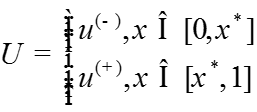
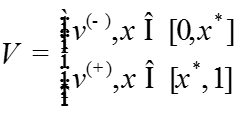
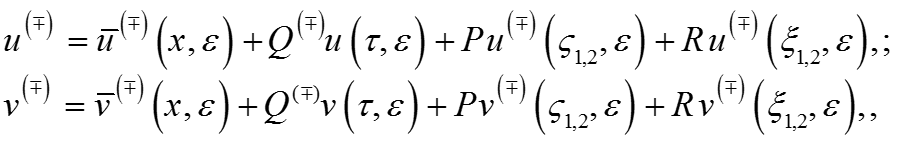
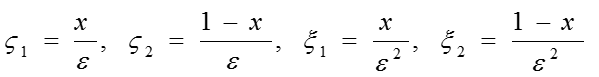
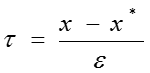
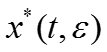
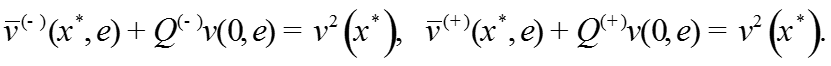
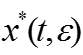
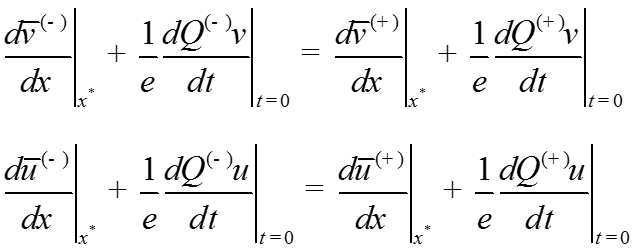
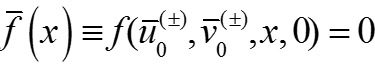
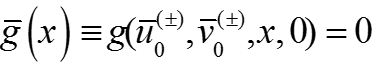
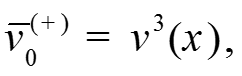
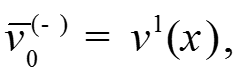
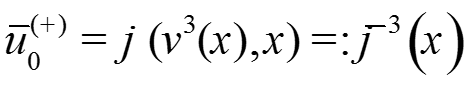
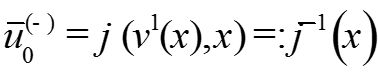
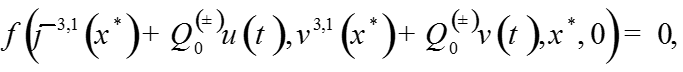
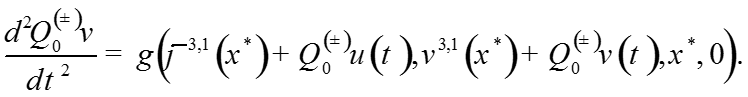
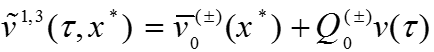
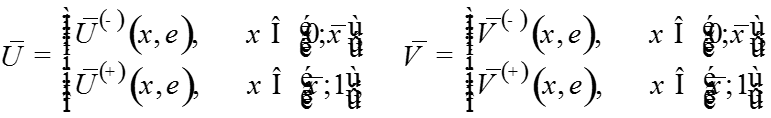
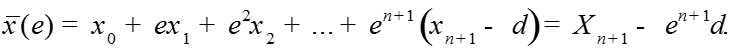
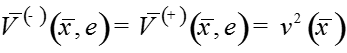
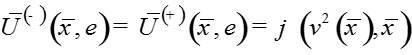
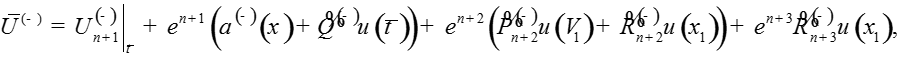
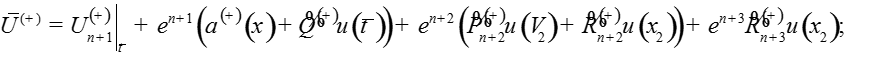
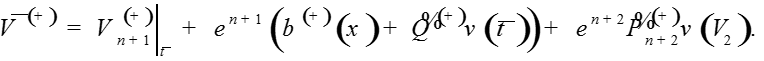
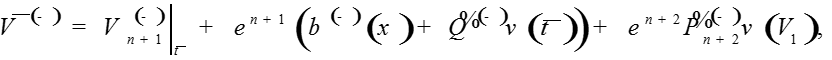
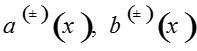
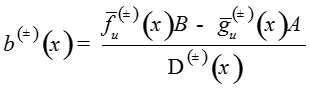
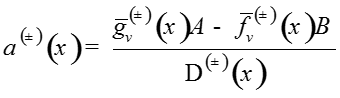
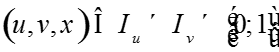
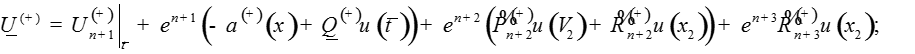
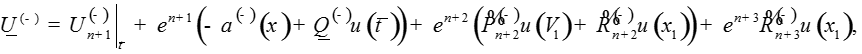
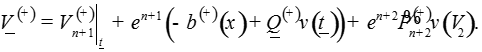
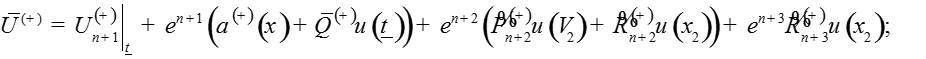
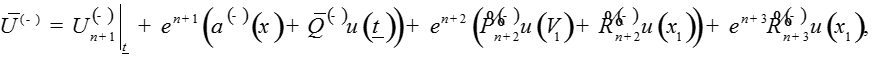
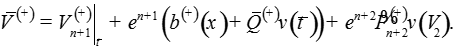
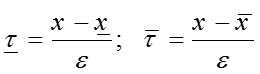