7. Максимальное значение регулируемой величины h=0.46
· Построим АЧХ системы и определим косвенные показатели качества:
 |
в
передаточной функции системы
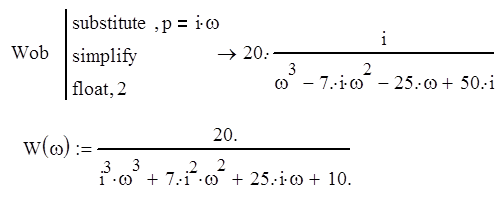График АЧХ будет иметь вид:
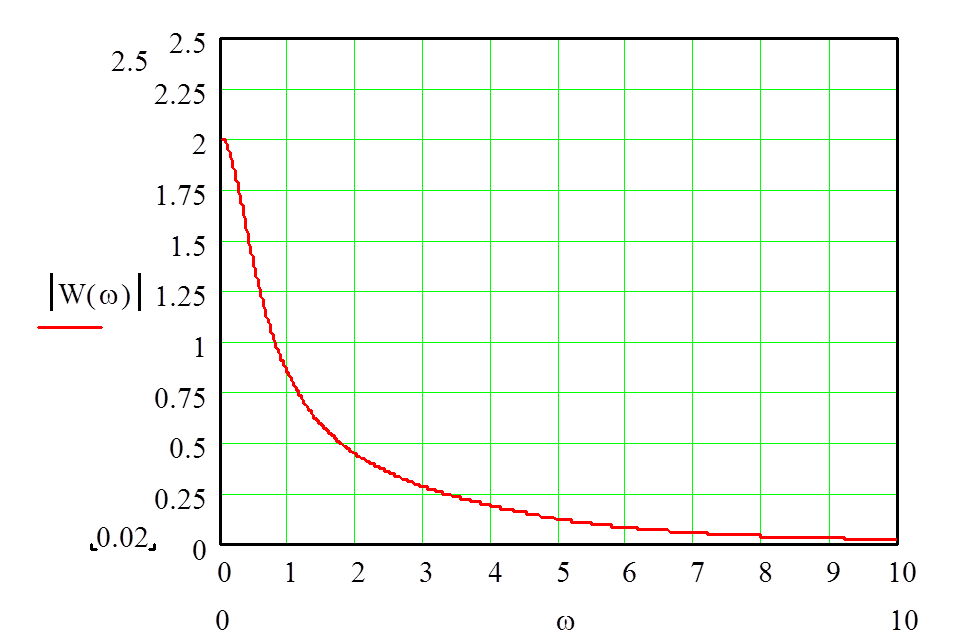
рисунок 5 - график АЧХ системы
Определим косвенные показатели качества:
1. Частота
среза w=4,5 (при значении амплитуды 0,1*А
)
2. Колебательность системы М=1
3. Полоса
пропускания: для ее определения считается значение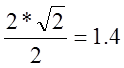 
Определяем значение частот при амплитуде 1.4: w1=0 w2=0.5
4. Значение амплитуды при нулевой частоте: А0=2
5. Максимальное значение амплитуды: Amax=2
6. 
Период колебаний:
7. Перерегулирование: d=15%
· Построим логарифмические характеристики системы: ЛФЧХ есть ФЧХ рассматриваемая как функция ln(ω). Для построения этих характеристик воспользуемся средой MATLAB.
s=zpk('s');w=20/(s^3+7*s^2+25*s+50) – создание ЗПК объекта
Zero/pole/gain:
20
--------------------------------
(s+3.878) (s^2 + 3.122s + 12.89)
>> sisotool(w)
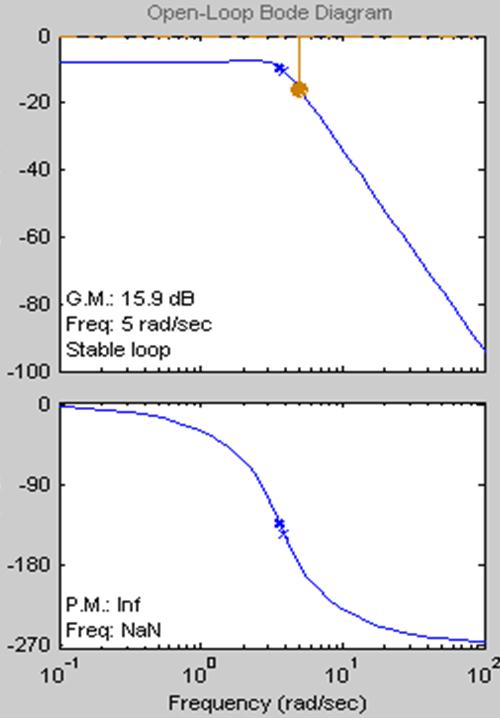
рисунок 6 –график ЛФЧХ и ЛАЧХ системы
Из графиков видно:
· запас устойчивости по фазе составляет γС=50
· запас устойчивости по амплитуде LЗАП=15.9 дБ
В ходе первой части курсовой работы была найдена общая передаточная функция системы, построены графики переходного процесса, АЧХ, ЛФЧХ и ЛАЧХ. Анализ показателей качества показывает, что система весьма точна в регулировании и не имеет колебаний. Однако другие характеристики говорят о низком запасе устойчивости по фазе, что весьма неблагоприятно скажется на управлении системы при изменении некоторых параметров управления. Данную ситуацию простым изменением коэффициентов исправить не удалось, есть вероятность, что требуется ввод дополнительных звеньев. Достаточно большой запас устойчивости по амплитуде дает шанс серьезного изменения коэффициентов усиления основной схемы, без потери устойчивости.
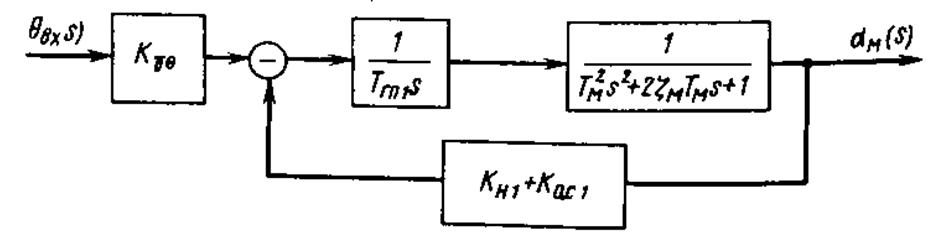Введем в систему нелинейный элемент –
гидравлическое реле. Характеристика данного реле содержит зону
нечувствительности (рисунок 8).
Рисунок 7 – система гидропривода с нелинейным элементом
 |
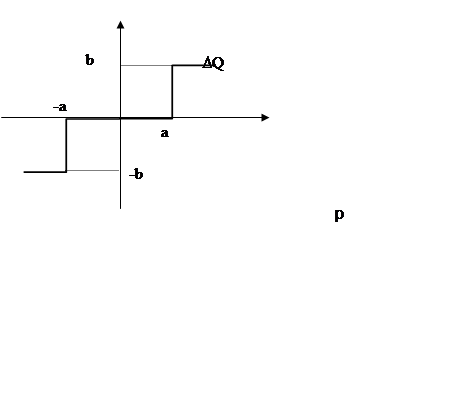Рисунок 8 – характеристика гидравлического реле
Данное реле работает следующим образом: насос подает количество жидкости на гидромотор, но до него не доходит до тех пор пока давление не достигнет значения а или –а.
Такая характеристика соответствует следующей системе:
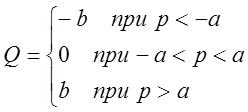(4.1)
где p – давление на входе гидравлического реле, Q-количества жидкости на выходе гидравлического реле. Для реализации задания, по построению фазового портрета примем следующие значения для b и a:
а=0,5 Па, b=5 м3/c (4.2)
На вход гидравлического реле с сумматора поступает разность давлений DP=Pзад-Pо.с (см. рис.8). Будем считать, что разность давлений системы P=0. Обозначим сигнал на выходе линейной части x=P(S) Тогда на вход нелинейного элемента будет поступать сигнал DР =-x, а на вход линейной части x1=F(DР)= F(-x). Преобразуем исходную систему (см. рисунок 7) в одноконтурную систему с последовательно соединенными нелинейной и линейной частями (рисунок 8).
|
|
 |
|||
|
|||
Линейная часть разомкнутой системы будет иметь следующую передаточную функцию:
>> W=w1*w2*w3*w4
Zero/pole/gain:
4
--------------------------
(0.04s^2 + 28s + 1)
На основании системы 4.1 и условий 4.2, имеет следующий вид:
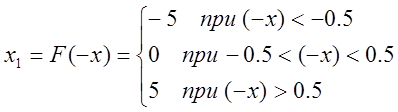(5.1)
Воспользовавшись передаточной функцией линейной части и релейной зависимостью F(-x), найдем дифференциальное уравнение, описывающее систему.
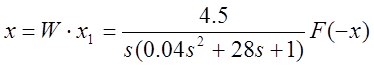(5.2)
Так как релейная характеристика элемента нечетная, то F(-x)=-F(x). Тогда получим:
(5.3)
Перехода в 5.3 к дифференциальному виду имеем:
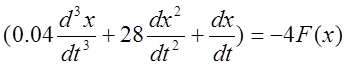(5.4)
Введем замену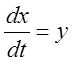 
Так как фазовый портрет строится на плоскости, отбросим члены у которых показатель степени выше 2:
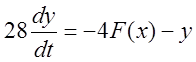(5.5)
Преобразуя (5.5) получим:
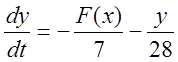
Для построения фазового портрета перейдем к дифференцированию
по переменной x (вводя замену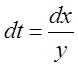 
):
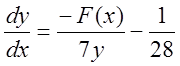(5.6)
Воспользовавшись системой 5.1, находим аналитическое значение выражения F(x):
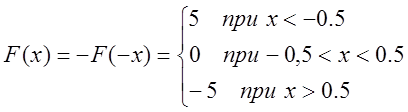(5.7)
Применяя полученную систему 5.7 к уравнению 5.6, получаем следующую зависимость:
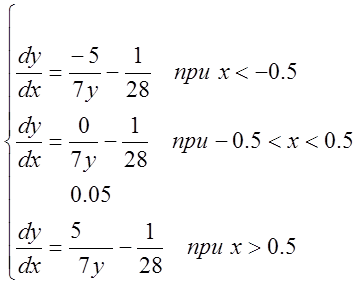(5.8)
Для построения фазовых траекторий на плоскости, воспользуемся программным математическим пакетом Mathcad. Зададим вектор начальных условий:
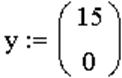
Определим функцию D по 3-м линейным участкам нелинейной статической характеристики (см (5.8)) Для этого применяем метод условного программирования.
Построим траекторию на фазовой
плоскости, предполагая, что первый столбец матрицы решения 
содержит точки, в которых ищется
решение дифференциального уравнения, второй 
-
содержит значения найденного решения, то есть y(t) и, наконец, третий столбец 
содержит первые производные этого
решения, то есть dy(t)/dt.
 |
Найдем матрицу решения заданной функции.
На рисунке 9 приведен полученный фазовый портрет.
 |
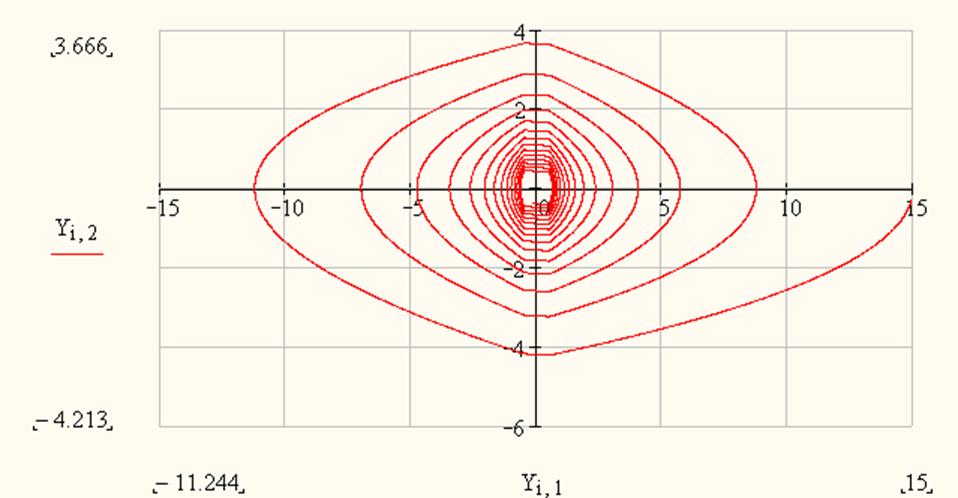рисунке 9 – фазовый портрет САР
 |
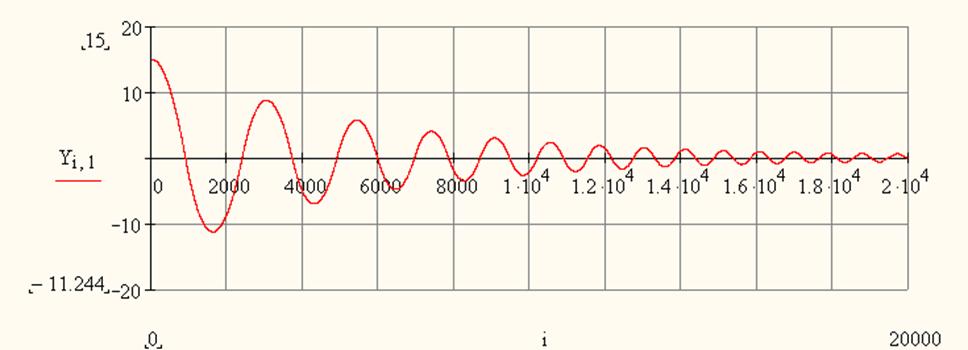рисунке 10 – график переходного процесса САР
Из графика переходного процесса и фазового портрета можно сделать вывод, что колебания в системе носят затухающий характер, с большим показателем времени затухания. Из точки, соответствующей начальным условиям, система движется в точку, где она находится в некотором равновесном состояние. Это является достаточным для нормального функционирования системы.
В результате исследование линейной системы автоматического регулирования угла поворота вала гидродвигателя можно сделать вывод, что рассматриваемая система при выбранных параметрах звеньев структурной схемы является устойчивой.
При вводе элемента, имеющего нелинейную характеристику, система будет стремится к некоторому равновесному состоянию. Такие выводы сделаны на основании исследования фазовых траекторий и графика переходного процесса.
Таким образом в ходе курсовой работы были изучены методы анализа линейных и нелинейных систем, рассмотрены их показатели качества и сделаны выводы по характеру их работы.
1. Попов Д.Н. Динамика и регулирование гидро- и пневмосистем. – М.: Машиностроение, 1987. 464 с.: ил.
2. Основы автоматического регулирования/Под ред. В.С. Пугачева. – М.: Наука, 1974. – 720 с.: ил.
3. Дифференциальное и интегральное исчисления; Пискунов Н. С. – М. Высшая школа. 1961 г.- 460 с.: ил.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.