
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНСТИТУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
Лабораторная работа №4
ИССЛЕДОВАНИЕ САУ НА ФАЗОВОЙ ПЛОСКОСТИ
Выполнил:
ст. гр. УИТ-42
Синегубов А.А
Проверил: Мефедова Ю. А.
Балаково 2004
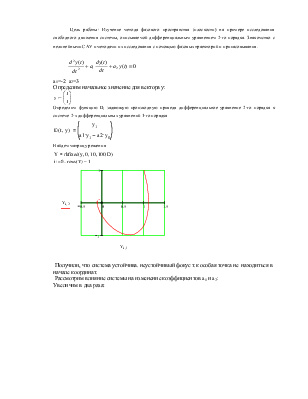
Цель работы: Изучение метода фазового пространства (плоскости) на примере исследования свободного движения системы, описываемой дифференциальным уравнением 2-го порядка. Знакомство с нелинейными САУ и методами их исследования с помощью фазовых траекторий и припасовывания.
|
|
a1=-2 a2=3
Определим начальное значение для вектора у:
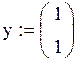
Определим функцию D, задающую производную приведя дифференциальное уравнение 2-го порядка к системе 2-х дифференциальных уравнений 1-го порядка
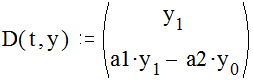
Найдем матрицу решения
![]()
![]()
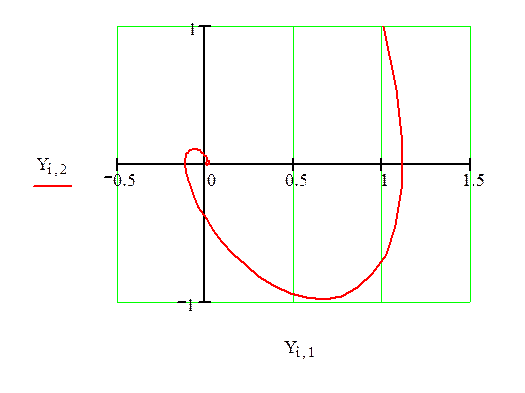
Получили, что система устойчива. неустойчивый фокус т.к особая точка не находиться в начале координат.
Рассмотрим влияние системы на изменение коэффициентов a1 и a2:
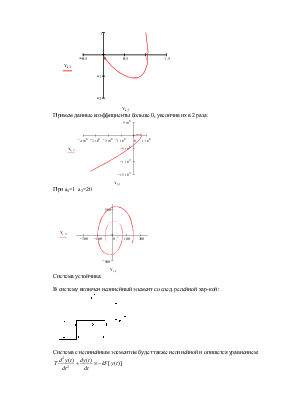
Увеличим в два раза:
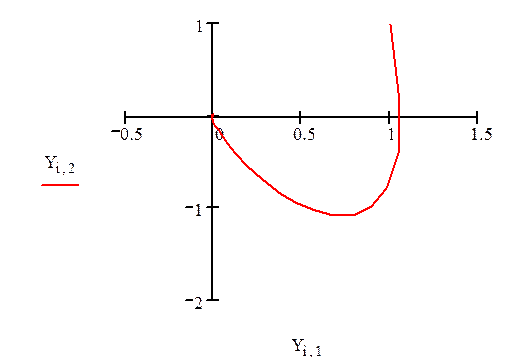
Примем данные коэффициенты больше 0, увеличив их в 2 раза:
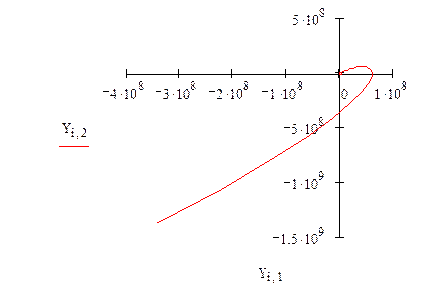
При a1=1 a2=20
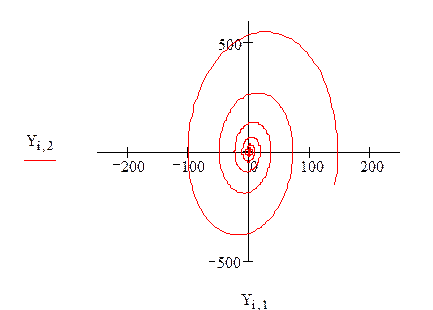
Система устойчива.
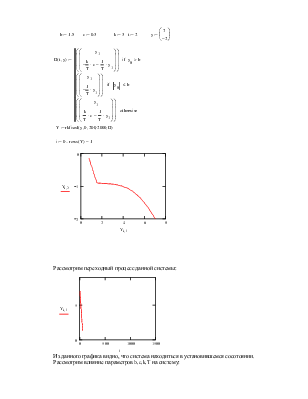
В систему включен нелинейный элемент со след. релейной хар-кой:
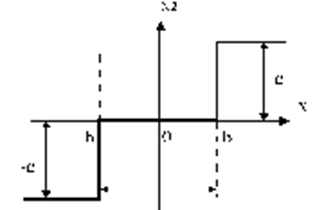
Система с нелинейным элементом будет также нелинейной и
опишется уравнением: 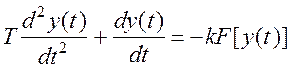
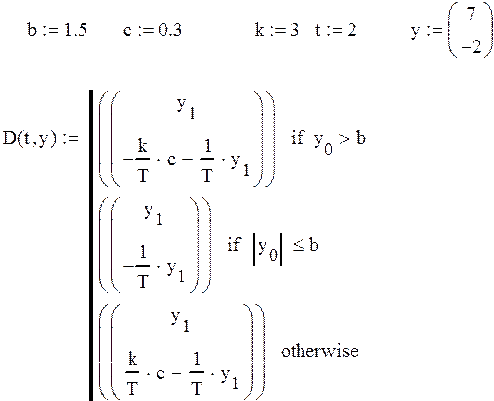
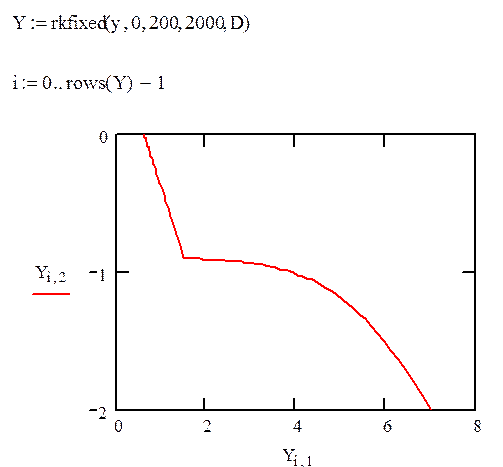
Рассмотрим переходный процесс данной системы:
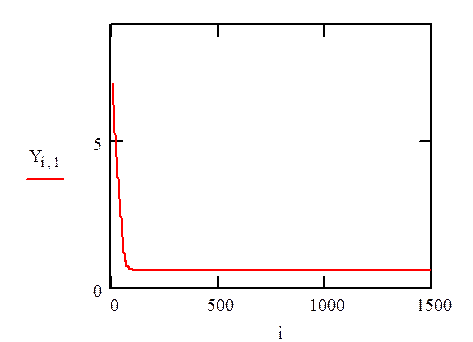
Из данного графика видно, что система находиться в установившемся сосотоянии.
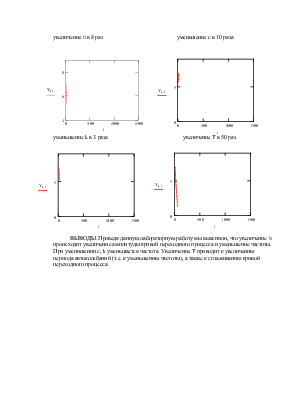
Рассмотрим влияние параметров b,c,k,T на систему:
увеличение b в 8 раз уменьшение с в 10 раза
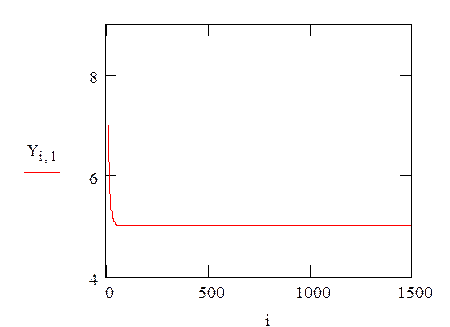
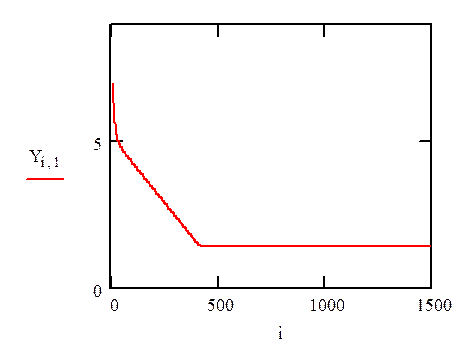
уменьшение k в 3 раза увеличение Т в 50 раз
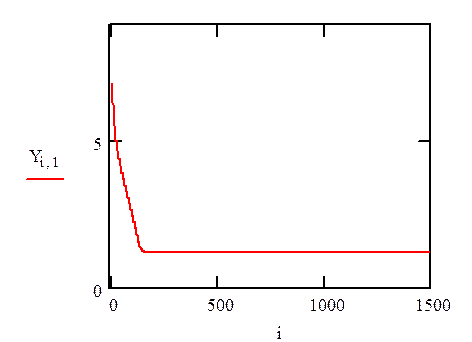

ВЫВОДЫ. Проведя данную лабораторную работу мы выяснили, что увеличение b происходит увеличение амплитуды кривой переходного процесса и уменьшение частоты. При уменишении с, k уменьшается частота. Увеличение Т приводит к увеличению периода автоколебаний (т.е. к уменьшению частоты), а также к сглаживанию кривой переходного процесса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.