Тарировка датчика. Средняя дисперсия выходного параметра в опытах матрицы, страница 5

1	0,1	103,183	0,971	5,317	84,786	121,580
2	0,2	116,666	0,824	5,292	98,355	134,976
3	0,3	130,149	0,693	5,273	111,903	148,394
4	0,4	143,631	0,590	5,261	125,429	161,833
5	0,5	157,114	0,530	5,254	138,934	175,294
6	0,6	170,596	0,530	5,254	152,416	188,776
7	0,7	184,079	0,590	5,261	165,877	202,281
8	0,8	197,562	0,693	5,273	179,316	215,807
9	0,9	211,044	0,824	5,292	192,734	229,355
10	1	224,527	0,971	5,317	206,130	242,924

По графику, показанном на рисунке 3.4, видно, что все индивидуальные значения выходного параметра попадают в доверительную зону, т.е. располагаются между линиями  и .

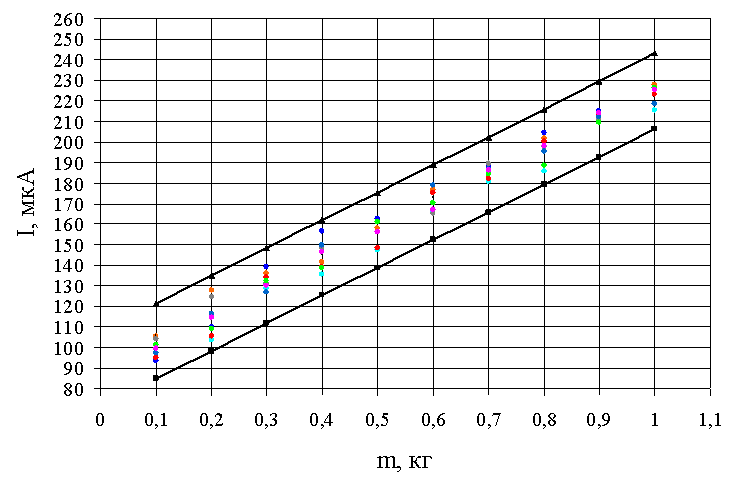
Рисунок 3.4 – Доверительные интервалы для индивидуальных значений выходного параметра

Определим погрешность, вносимую датчиком при измерении. Коэффициент  формулы (3.1) находится по следующему выражению [2]:

                                              (3.26)

где  – угол, показанный на рисунке 3.5.

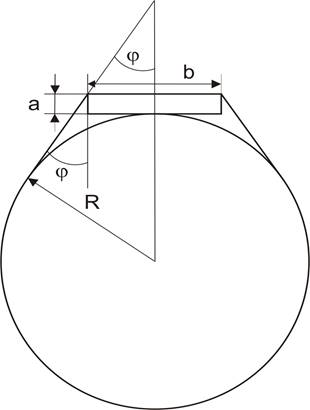
Рисунок 3.5 – Расположение датчика на цилиндрической поверхности

Определим выражение для расчета .

По рисунку 3.5 записываем соотношение:

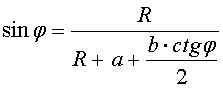                                        (3.27)

Преобразуем выражение (3.27) таким образом, чтобы в него входил .

                                    (3.28)

                                   (3.29)

Введем в выражении (3.29) замену .

                                       (3.30)

Решим уравнение (3.30) относительно .

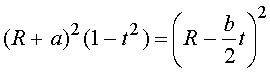                                (3.31)

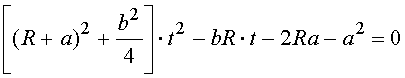                   (3.32)

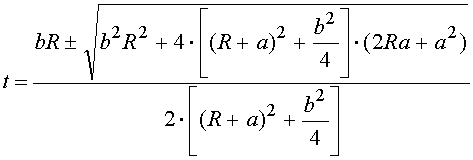                  (3.33)

Поскольку угол  изменяется от 0 до 90⁰, т.е. , то принимаем во внимание только положительный корень уравнения (3.30). Тогда выражение для вычисления  имеет вид:

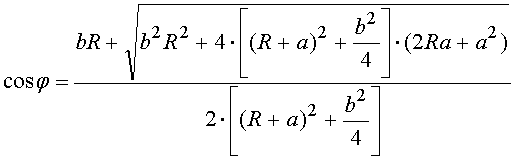           (3.34)

Коэффициент  находится по формуле (3.35).

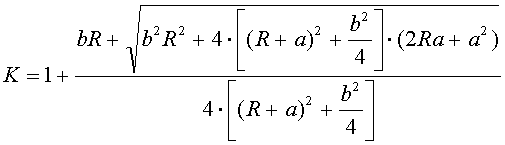            (3.35)

Подставляя численные значения  и , получим зависимость  от радиуса тела  (в миллиметрах) в месте измерения:

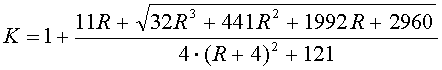             (3.36)

Рассчитаем значение коэффициента  при максимальном и минимальном радиусах тела:

- при  ;

- при  .

Действительное давление изделия на тело в месте измерения будет меньше измеряемого датчиком в  раз. Т.е. относительная погрешность из-за собственных размеров датчика . Данная погрешность относится к классу систематических.

Значение  при тарировке датчика .

Подставляя в формулу (3.1) числовые значения, находим зависимость между давлением и массой грузов:

                                                (3.37)

где  – давление на датчик, кПа;

 – масса грузов, кг.

С учетом перевода величины массы грузов в величину давления регрессионное уравнение (3.12) запишется в виде:

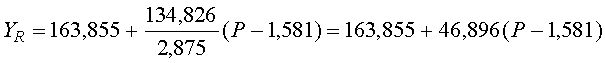.          (3.38)

Уравнение (3.38) представляет собой регрессионную зависимость величины измеряемого выходного тока от давления. По данному уравнению строится характеристика шкалы прибора, отградуированная в величинах давления (рисунок 3.6).

Поскольку датчик имеет разборную конструкцию, то возможно использование чувствительных элементов с различной жесткостью для измерения давления в разных диапазонах. В таком случае тарировку необходимо проводить для каждого чувствительного элемента. Чувствительный элемент, для которого проводилась тарировка пригоден для измерения давлений в диапазоне от 0,3 кПа до 2,9 кПа. Для проведения измерений больших давлений необходимы чувствительные элементы с большей жесктостью измерительной пружины.

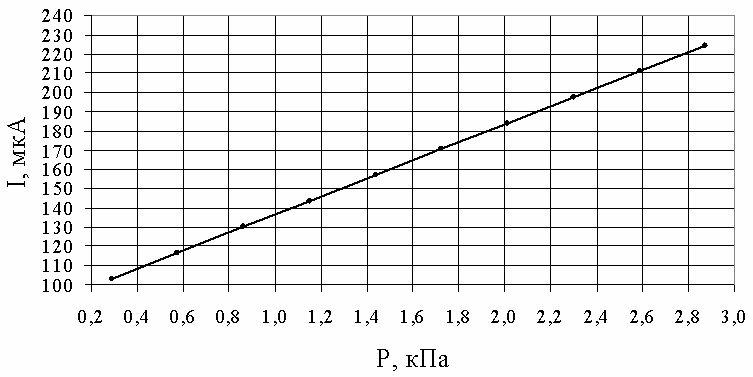
Рисунок 3.6 – Тарировочная характеристика прибора в величинах давления

Выводы по разделу

В данном разделе представлены данные экспериментальной тарировки датчика. В результате обработки данных получена линейная регрессионная модель шкалы прибора, определены коэффициенты регрессии, адекватность полученной зависимости, значимость коэффициентов регрессии и их доверительные интервалы, а также доверительные интервалы средних и индивидуальных значений выходного параметра при фиксированном значении фактора.

Также проведена оценка систематической погрешности, вносимой датчиком в измерения, найдена зависимость коэффициента, учитывающего эту погрешность, от радиуса тела при заданных размерах датчика.