Тарировка датчика. Средняя дисперсия выходного параметра в опытах матрицы, страница 2

Исключим резко выделяющиеся экспериментальные данные. Для определения данных, подлежащих исключению, используется статистический метод, который включает в себя следующую последовательность действий [11]:

- определение среднего значения и дисперсии для полученных значений случайных величин:

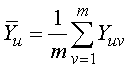;                                            (3.2)

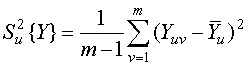;                                  (3.3)

где  – среднее значение выходной величины при значении фактора ;

 – дисперсия при значении фактора .

- определение расчетного значения критерия Смирнова-Грабса по формулам:

при подозрении резко выделяющегося максимального значения

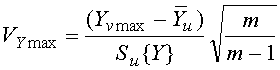                              (3.4)

при подозрении резко выделяющегося минимального значения

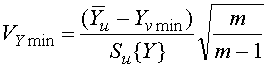.                               (3.5)

Затем  и  сравнивают с табличным критическим значением критерия , который определяется по специальным таблицам [11] при заданной доверительной вероятности  и количестве опытов . Если  или , то резко выделяющиеся значения и  и  исключают из дальнейшей статистической обработки данных.

Данные, обработанные по указанной методике, представлены в таблице 3.2.

При значении доверительной вероятности  и  значение критерия . Как видно из таблицы 3.2, все  и , т.е. данных, подлежащих исключению, нет.

Проверим гипотезу о нормальном распределении случайных величин . Проверка этой гипотезы для каждого -го опыта матрицы включает определение среднего значения , определение дисперсии выходного параметра для каждого опыта матрицы; определение расчетного критерия  по формуле 3.6.

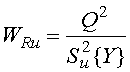;                                            (3.6)

где

;                    (3.7)

при четном значении  ;  . Значения  для ; приведены в таблицах [11].

После расчета значения критерия  его сравнивают с табличным значением . Если , то гипотеза о нормальном распределении случайных величин не отвергается.

Рассчитав значения , заносим их в таблицу 3.2.

Таблица 3.2 – Результаты обработки экспериментальных данных