Тарировка датчика. Средняя дисперсия выходного параметра в опытах матрицы, страница 4

Доверительные абсолютные ошибки коэффициентов регрессии вычисляем по формуле (3.19).

                                           (3.19)

Подставив значения, получим: , .

Доверительные интервалы для истинных значений коэффициентов регрессии ,  определяются неравенством (3.20).

                                  (3.20)

Доверительные интервалы коэффициентов регрессии: ;  или  и .

Определим доверительные интервалы средних значений выходного параметра при фиксированном значении фактора. Чтобы определить степень отклонения расчетных значений выходного параметра  от истинного его значения при каждом уровне фактра , определяем доверительные ошибки  расчетного значения выходного параметра и доверительные интервалы среднего значения выходного параметра.

Доверительные ошибки расчетных значений выходного параметра для каждого уровня фактора рассчитываем по формуле (3.21).

                                           (3.21)

где  – оценка среднего квадратического отклонения расчетного значения выходного параметра  для каждого значения , определяемого по формуле (3.22).

                      (3.22)

Зная ошибки расчетной величины, можно найти доверительные интервалы для истинных средних значений выходного параметра, используя следующее равенство:

       (3.23)

Результаты расчетов по указанной методике показаны в таблице 3.3

На основе данных, представленных в таблице 3.3, строим графики зависимости  и  (рисунок 3.3).

В область, ограниченную линиями  и  попадают средние экспериментальные значения . Любое сечение этой области прямой, параллельной оси ординат, соответствует доверительному интервалу, в котором с заданной вероятностью будет находиться истинное среднее значение выходного параметра .

Таблица 3.3. – Определение доверительных интервалов средних значений выходного параметра

1	0,1	0,2025	0,971	3,361	103,183	99,822	106,544
2	0,2	0,1225	0,824	2,851	116,666	113,815	119,516
3	0,3	0,0625	0,693	2,397	130,149	127,751	132,546
4	0,4	0,0225	0,590	2,040	143,631	141,591	145,671
5	0,5	0,0025	0,530	1,835	157,114	155,279	158,949
6	0,6	0,0025	0,530	1,835	170,596	168,761	172,431
7	0,7	0,0225	0,590	2,040	184,079	182,039	186,119
8	0,8	0,0625	0,693	2,397	197,562	195,164	199,959
9	0,9	0,1225	0,824	2,851	211,044	208,194	213,895
10	1	0,2025	0,971	3,361	224,527	221,166	227,888

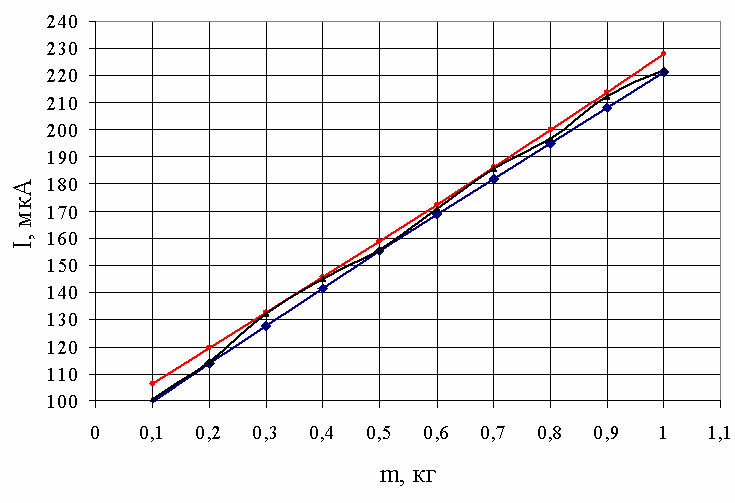
Рисунок 3.3 – Доверительные интервалы средних значений выходного параметра

Границы доверительного интервала для индивидуальных значений выходного параметра  при каждом уровне фактора  определяются по формулам:

                      (3.24)

                      (3.25)

где .

Результаты расчета границ доверительных интервалов для индивидуальных значений выходного параметра при каждом уровне фактора показаны в таблице 3.4.

Таблица 3.4 – Границы доверительных интервалов для индивидуальных значений выходного фактора