Тарировка датчика. Средняя дисперсия выходного параметра в опытах матрицы, страница 3

Табличное значение  при  и  равно 0,842. Поскольку  гипотеза о нормальном распределении не отвергается. Это первое условие возможности проведения регрессионного анализа.

Проведем проверку гипотезы об однородности дисперсий в опытах матрицы. Так как число повторных опытов () одинаково для всех опытов матрицы, то для проверки однородности дисперсий применяется критерий Кочрена, расчетное значение которого:

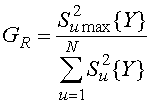.                                         (3.8)

Расчетное значение  сравнивается с табличным значением , которое определяется в зависимости от числа опытов в матрице  и числа степеней свободы дисперсии  для заданной доверительной вероятности.

В рассматриваемом случае , . Т.к. , то гипотеза об однородности дисперсий, т.е. равноточности и воспроизводимости опытов не отвергается.

Определим среднюю дисперсию выходного параметра в опытах матрицы. Средняя дисперсия определяется по формуле (3.9).

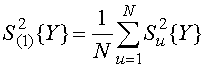.                                          (3.9)

Число степеней свободы этой дисперсии равно:

.                                    (3.9)

В результате расчетов получаем ; .

Средняя дисперсия (дисперсия воспроизводимости) характеризует средний разброс значений выходного параметра относительно его средних значений при каждом уровне факторов, т.е. ошибку опытов в эксперименте.

Определим подходящий вид регрессионной модели графическим методом. Для этого построим график зависимости среднего значения выходного параметра  от значения фактора (рисунок 3.2).

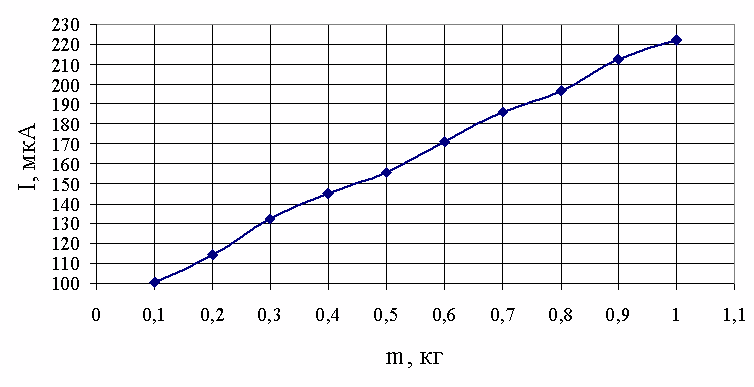
Рисунок 3.2 – График экспериментальной зависимости

По виду полученного графика выбираем линейный вид регрессионной модели. В этом случае для описания экспериментальных данных можно условно принять уравнение прямой линии:

.                               (3.10)

где .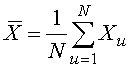

Определим значения коэффициентов регрессии по формулам:

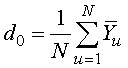;                                            (3.10)

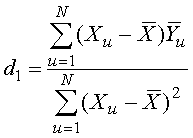.                                            (3.11)

В результате расчета получаем следующие коэффициенты линейной регрессии: ; . Уравнение регрессии будет иметь вид:

.                               (3.12)

Определим адекватность полученной регрессионной модели используя критерий Фишера, расчетное значение которого определяется по формуле 3.13.

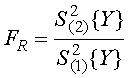,                                             (3.13)

где  – средняя дисперсия или дисперсия воспроизводимости, определяемая по формуле (3.9);

 – дисперсия, характеризующая рассеивание средних экспериментальных значений  относительно прямой линии, определяемой по формуле (3.10).

Дисперсия  характеризует точность аппроксимации зависимости  прямой линии и определяется по следующей формуле:

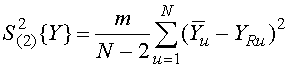,                           (3.13)

Число степеней свободы этой дисперсии . Расчетное значение  сравнивают с табличным значением критерия Фишера , которое определяют для заданной доверительной вероятности и числе степеней свободы дисперсий  и . Если , то гипотеза об адекватности линейного уравнения опытным данным не отвергается.

В результате расчетов получаем: , ; . Находим табличное значение критерия Фишера при ; ;   .

Т.к. , то гипотеза об адекватности полученного линейного уравнения экспериментальным данным не отвергается.

Определим значимость коэффициентов регрессии и их доверительные интервалы. Для оценки значимости коэффициентов регрессии используется критерий Стьюдента, расчетное значение которого определяется по формуле (3.14).

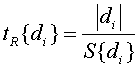                                            (3.14)

где  – оценка среднего квадратического отклонения коэффициента регрессии .

Для оценки дисперсий коэффициентов регрессии  и  в уравнении (3.10) используются следующие формулы:

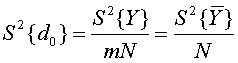                                     (3.15)

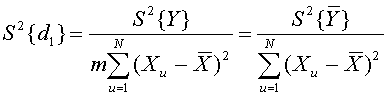                      (3.16)

В формулы (3.15) и (3.16) входит дисперсия , которая является сводной оценкой дисперсии случайной величины  выходного параметра. Эта дисперсия определяется по следующей формуле:

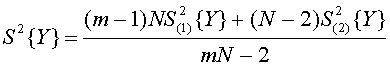                      (3.17)

Число степеней свободы этой дисперсии

                                         (3.18)

В результате расчета, получаем:

- сводная дисперсия случайной величины: ;

- число степеней свободы сводной дисперсии: ;

- дисперсии коэффициентов регрессии , ;

- расчетные значения критерия Стьюдента: , .

Табличное значение критерия Стьюдента при  и  . Поскольку  и , полученные коэффициенты регрессии значимы и, следовательно, и связь между  и  значима.