Физика \ Физика

Расчётная часть курсового проекта. Погрешность измерительного канала

7 страниц (Word-файл)

4 Расчётная часть проекта

Исходные данные:

Измеряемая среда – конденсат.

Внутренний диаметр трубопровода, округленный по ГОСТу до стандартного при температуре 20˚С, D₂₀=50 мм.

Номинальный массовый расход сетевой воды, Q_ном=13.

Абсолютное давление среды перед сужающим устройством, Р=3 МПа.

Температура воды перед сужающим устройством, t=50˚С.

Материал трубопровода – сталь 12Х17.

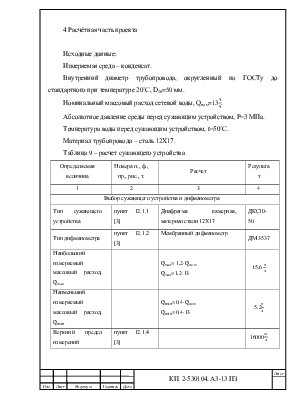
Таблица 9 – расчет сужающего устройства

Определяемая величина	Номера п., ф., пр., рис., т.	Расчет	Результат
1	2	3	4
Выбор сужающего устройства и дифманометра
Тип сужающего устройства	пункт 12.1.1 [3]	Диафрагма камерная, материал стали 12Х17	ДКС10-50
Тип дифманометра	пункт 12.1.2 [3]	Мембранный дифманометр	ДМ 3537
Наибольший измеряемый массовый расход,		= 1,2· =1,2·13	15,6
Наименьший измеряемый массовый расход,		=0,4· =0,4·13	5,2
Верхний предел измерений дифманометра,	пункт 12.1.4 [3]		16000

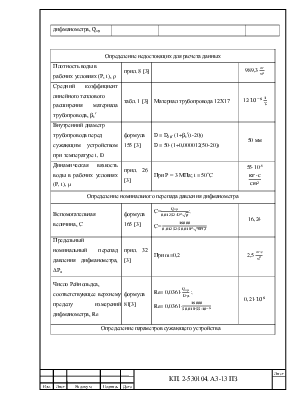
Определение недостоющих для расчета данных
Плотность воды в рабочих условиях (Р, t), ρ	прил. 8 [3]		989,3
Средний коэффициент линейного теплового расширения материала трубопровода,	табл. 1 [3]	Материал трубопровода 12Х17	12·
Внутренний диаметр трубопровода перед сужающим устройством при температуре t, D	формула 155 [3]	=·(1+(t-20)) = 50·(1+0,000012(50-20))	50 мм
Динамическая вязкость воды в рабочих условиях (P, t), µ	прил. 26 [3]	При Р = 3 МПа; t = 50˚С	55·10^-6
Определение номинального перепада давления дифманометра
Вспомогательная величина, С	формула 165 [3]	С=; С=	16,24
Предельный номинальный перепад давления дифманометра, ∆	прил. 32 [3]	При m=0,2	2,5
Число Рейнольдса, соответствующее верхнему пределу измерений дифманометра, Re	формула 81[3]	Re= 0,0361· ; Re= 0,0361·	0,21·
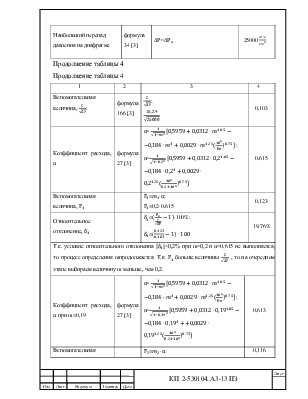
Определение параметров сужающего устройства
Наибольший перепад давления на диафрагме	формула 34 [3]	∆Р=∆	25000

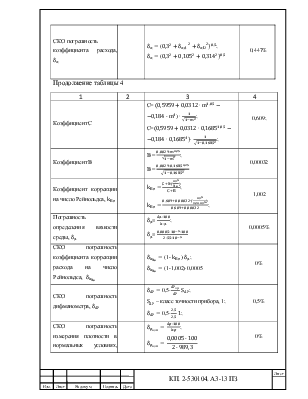
Продолжение таблицы 4

1	2	3		4
Вспомогательная величина, ;	формула 166 [3]	;		0,103
Коэффициент расхода, α	формула 27 [3]	α= ; α=		0,615
Вспомогательная величина,		=·α; =0,2·0,615		0,123
Относительное отклонение,		=·100%; =(		19,76%
Т.к. условие относительного отклонения ˂0,2% при m=0,2 и α=0,615 не выполняется, то процесс определения mпродолжается. Т.к. больше величины , то на очередном этапе выбираем величину m меньше, чем 0,2.
Коэффициент расхода, α при m=0,19	формула 27 [3]	α= ; α=	0,613
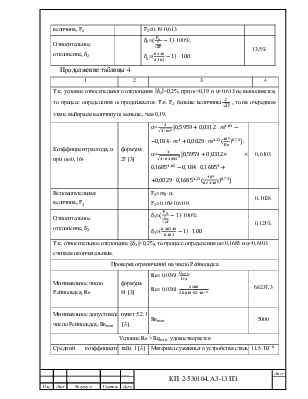
Вспомогательная величина,		=·α; =0,19·0,613	0,116
Относительное отклонение,		=·100%; =(	13,5%