Проектирование привода рабочей машины, страница 6

Рассчитываем изгибающие моменты по нагруженным участкам вала в горизонтальной плоскости YAZ:

, ,

, ,

, , .

, ,

, , ,

, , .

По полученным значениям строим эпюру изгибающих моментов (рис. 3, д).

Определяем величины суммарных изгибающих моментов в сечениях вала (точки 1…3):

,

,

, ,

,

.

По полученным значениям строим эпюру изгибающих моментов (рис. 3, е).

Строим эпюру крутящих моментов Т, определяя по схеме привода нагруженные участки вала (рис. 3, ж).

Находим опасное сечение по величине  и Т на эпюрах. Из рис. 3 видно, что опасное сечение находится под шестерней, т.к в этом сечении максимальное значение изгибающего момента и наличие крутящего момента.

Эквивалентный момент в этом сечении равен:

,

,

Уточняем диаметр вала в опасном сечении под шестерней, принимая допускаемое напряжение при изгибе , МПа:

,

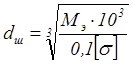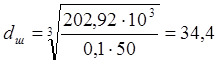, мм.

Расчет показал, что диаметр вала под шестерней необходимо уменьшить по сравнению с ранее принятым , мм. По ГОСТу принимаем , мм.

6.2. Выходной вал редуктора

Строим общую расчетную схему нагружения вала (рис 4, а). Направление сил в зацеплении зубчатых колес и в открытой передаче определяем по рисунку в задании.

Вычерчиваем схему нагружения вала в вертикальной плоскости XAZ, представляя его в виде балки на двух опорах – А и В (рис 4, б).

Рассчитываем реакции опор в точках А и В из условий равновесия:

,

,

,

, Н.

,

,

,

,  Н.

Выполняем проверку:

Определяем изгибающие моменты по нагруженным участкам вала в вертикальной плоскости XAZ:

, ,

, ,

, , .

, ,

, ,

, , .

Строим эпюру изгибающих моментов в вертикальной плоскости (рис. 4, в)

Вычерчиваем схему нагружения вала в горизонтальной плоскости YAZ, для чего совмещаем плоскость YAZ с плоскостью чертежа (рис. 4, г).

Определяем реакции опор в плоскости YAZ:

,

,

,

, Н.

,

,

,

, Н.

Выполняем проверку:

Рассчитываем изгибающие моменты по нагруженным участкам вала в горизонтальной плоскости YAZ:

, ,

, ,

, , .

, ,

, ,

, , .

По полученным значениям строим эпюру изгибающих моментов (рис. 4, д).

Определяем величины суммарных изгибающих моментов в сечениях вала (точки 1…4):

,

,

, ,

По полученным значениям строим эпюру изгибающих моментов (рис. 4, е).

Строим эпюру крутящих моментов Т, определяя по схеме привода нагруженные участки вала (рис. 4, ж).

Находим опасное сечение по величине  и Т на эпюрах. Из рис. 4 видно, что опасное сечение расположено под зубчатым колесом.

Эквивалентный момент в этом сечении равен:

 .

Уточняем диаметр вала в опасном сечении под зубчатым колесом, принимая допускаемое напряжение при изгибе , МПа:

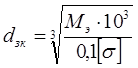
мм

Расчет показал, что диаметр вала под колесом необходимо уменьшить по сравнению с ранее принятым , мм. По ГОСТу принимаем , мм. Корректируем диаметры остальных участков вала: , мм; , мм;  мм;  , мм; , мм.

  6.3 Уточнённый расчёт выходного вала на усталостную прочность.

Этот расчёт уточняет результаты проверочного расчёта выходного вала редуктора и заключается в определении коэффициента запаса прочности n в опасном сечении вала. В данном случае учитываются дополнительные концентраторы напряжения, которые не были учтены в предыдущем расчёте на статическую прочность.

Условие прочности имеет вид:

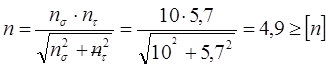
Где

коэффициент запаса прочности в опасном сечении;

коэффициенты запаса прочности по нормальным и касательным напряжениям;

(1,5…4,0)-рекомендуемый коэффициент запаса прочности .

  

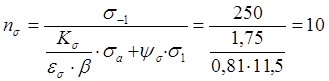
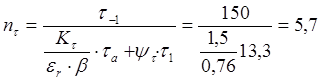
Где

,- пределы выносливости при изгибе и кручении ,МПа;

,- эффективные коэффициенты концентрации напряжений при изгибе и кручении;

,-масштабные коэффициенты;

- коэффициент поверхностного упрочнения , =1 ;

,-амплитудные значения нормальных и касательных напряжений, МПа;

,- средние значения нормальных и касательных напряжений, МПа;