Разработка цифрового спектронализатора. Расчетно-пояснительная записка, страница 3

Так как близким по частоте гармоническим составляющим сигнала s(t) должна соответствовать в наблюдаемом спектре последовательность максимумов G_u(f), разделенных провалами, то для корректного отображения соседних гармонических компонент помимо двух отсчетов - максимумов спектра - необходим по меньшей мере один отсчет, соответствующий минимуму. Поэтому теоретическим пределом разрешающей способности Df  при классической методике спектрального оценивания служит величина Df_min = 2×f₁  [8]. С другой стороны, из-за значительной ширины главного лепестка спектра весовой функции минимально необходимый для четкого разрешения частотный интервал между спектральными составляющими будет равен (J_D/2 + 1)×f₁.

Таким образом, спектроанализатор обеспечивает разрешающую способность по частоте

,  Гц.

Отсюда требуемый частотны разнос дискретных компонентов спектра

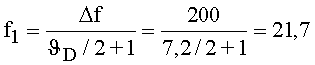Гц,

и время накопления сигнала

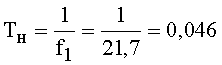 с =46 мс.

Это время примерно в два раза превышает допустимое время одного цикла анализа не более =28 мс. ). Поэтому для расчета спектра нужно использовать исходные данные из нескольких последовательных блоков памяти, обновляя при каждом цикле анализа лишь небольшую их часть, содержащуюся в одном очередном блоке.  В результате обновленные спектральные данные будут поступать через интервал времени

T_{А парал 2}  =  Т ∙ N_блока.

Число отсчетов .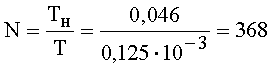

С учетом требований реализации быстрого преобразования Фурье (по степеням 2) принимаем N=512. При этом, уточненное время накопления составит

.

Найдем время вычислений спектра. Продолжительность цикла анализа не может быть меньше времени, затрачиваемого на преобразование набора отсчетов из временной области в частотную. Конкретное время расчета зависит от быстродействия аппаратуры, размерности N и выбранного алгоритма преобразования; приближенно оно может быть оценено по формуле

t_расч(N) = A_r(N) × t_Å + M_r(N) × t_Ä , где t_Å - длительность операции суммирования, t_Ä - длительность операции умножения, A_r(N) и M_r(N) - общее количество вещественных сложений и умножений. Для некоторых часто используемых алгоритмов величины A_r(N) и M_r(N) приведены в таблице 2.

Таблица 2 - Вычислительная сложность алгоритмов быстрого преобразования Фурье типа Кули-Тьюки

Основание преобразования	Общее число умножений Mr(N)	Общее число сложений Ar(N)
N = 2m (алгоритм 1)	N×(2×log2N – 7) + 12	3×N×(log2N –1) + 4
N = 4m	9/8×N×(log2N – 2)	N/8×(25×log2N – 18)

Используя табличные данные и требования технического задания, находим:

t_расч = (512×(2×log₂2048 – 7) + 12)× t_Å + (3×512×(log₂2048 –1) + 4) × t_Ä=

=0,0045 с=4,5 мс.

Полученное время является допустимым.

Так как  Т_н > Т_расч(N), то для записи поступающих данных выделим четыре блока памяти по 128 ячеек. В этом случае время цикла анализа будет равно

T_А= Т_н/4=16 мс,

что соответствует заданным требованиям.

Таким образом, необходимый интервал дискретизации Т, размерность преобразования Фурье N, весовая функция W(t) и параметры оперативного запоминающего устройства определены. Во втором и третьем разделах проводится подтверждение принятых технических решений методом математического  моделирования.