Электротехника \ Основы радиоэлектроники и связи

Разработка цифрового спектронализатора. Расчетно-пояснительная записка, страница 2

Gu(f)  =  0.5×S0×Gw( f+F0 )  +  0.5×S0×Gw( f-F0 ).

Наличие в зависимости Gu(f) боковых лепестков, величина которых определяется спектральной плотностью Gw(f) используемой весовой функции w(t), существенно осложняет спектральное оценивание. Ведь если анализируемый сигнал s(t) содержит на самом деле не одну, а несколько гармоник различной амплитуды, то функция Gu(f) будет представлять собой, соответственно, сумму соответствующих откликов на каждую из имеющихся гармоник. Отличить же в результирующей зависимости Gu(f) центральные лепестки, порождаемые присутствующими в s(t) слабыми гармониками, от боковых лепестков, порождаемых более мощными спектральными составляющими, невозможно. Таким образом, значительная величина боковых лепестков спектра весовой функции приводит на практике к ложному обнаружению спектральных составляющих анализируемого колебания.

В таблице 1 приведены наиболее употребительные оконные функции, применяемые при спектральном анализе.

Если разброс амплитуд гармонических составляющих сигнала не превышает

Ds = 20 lg( Smin / Smax )    дБ, где Smax - амплитуда наибольшей, а Smin - наименьшей спектральной составляющей сигнала, то используя функцию w(x) с уровнем боковых лепестков

D ≤ Ds, и игнорируя при анализе получаемого спектра    все локальные максимумы, отличающиеся от уровня глобального максимума более чем на  D  децибелл, можно гарантировать, что каждый из учитываемых спектральных всплесков будет соответствовать одной или нескольким маскирующим друг друга гармоническим составляющим сигнала, но ни один боковой лепесток спектра w(x) не будет ложно принят за реальную компоненту сигнала.

Таблица 1 - Весовые функции при спектральном оценивании и их параметры

Весовая функция во временной области w(x), |x| £ 0.5

Параметры

Уровень боковых лепестков D окна, дБ

Относительная ширина спектра окна, JD

Нормированная разрешающая способность Dfw

Прямоугольная,  w(x) = 1

1

-13

1,64

2,0

Хеннинга,  w(x) =

m = 3

-39,3

4,78

3,39

m = 4

-46,7

5,80

3,90

Хемминга, w(x) =

-

-42,7

3,82

2,91

Кайзера-Бесселя, w(x) =

a = 2,7

-62,5

5,66

3,83

a = 3,1

-72,1

6,42

4,21

a = 3,5

-81,8

7,20

4,60

Блекмана-Херриса,

W(x) =

a0 = 0,35875;

a1 = 0,48829

a2 = 0,14128;

a3 = 0,01168

-92,0

7,90

4,95

Исходя из технического задания оконная функция должна иметь уровень боковых лепестков ниже минус 78 дБ. Поэтому выбираем функцию Кайзера-Бесселя с параметром a=3,5. При этом относительная ширина спектрального окна JD=7,2 и нормированная разрешающая способность Dfw=4,60.

В выражение для окна Кайзера-Бесселя входит модифицированная функция Бесселя, имеющая вид:

I0(z) ≈ 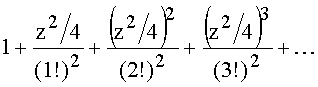    Далее определим требуемое время накопления (наблюдения) сигнала. Эта характеристика тесно связана с разрешающей способностью. Под разрешающей способностью по частоте (РСЧ) понимают способность спектроанализатора разделять (в частности, раздельно отображать) две соседние спектральные составляющие анализируемого воздействия.

Количественной мерой разрешающей способности служит наименьший интервал по частоте между спектральными составляющими Df, при котором число максимумов в наблюдаемом спектре однозначно определяется числом гармонических компонент в составе анализируемого колебания.

Скачать файл