Выделение областей устойчивых и неустойчивых состояний с помощью D-разбиения

7. Выделение областей устойчивых и неустойчивых состояний с по­мощью D-разбиения

Применение метода D-разбиения позволяет исследовать устойчи­вость замкнутой системы с помощью характеристического уравнения на плоскости, выделяя один или два параметра. В качестве таких параметров могут быть приняты передаточные коэффициенты  или постоянные времени передаточных функций

Рассмотрим

                                                          (67)

Из выражения (67) найдем:

                                                                (68)

Положим, что w – комплексное число, и отобразим мнимую ось плоскости корней    на плоскость w. Тогда при  из уравнения (67) получим

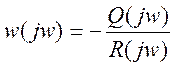                                                             (69)

или

Изменяя значения  w от до , построим в плоскости w(или и, v) кривую, отображающую мнимую ось jwплоскости Sна плос­кость w(jw). Получаемая в результате этого кривая является кривой D-разбиения. Такая кривая всегда симметрична относительно действитель­ной оси; поэтому можно строить лишь участок, соответствующий измене­нию чистоты от 0 до , а затем дополнить его зеркальным отображением кривой D-разбиения относительно действительной оси. В результате по­лучим несколько областей. Однако судить о том, в какой из областей все корни характеристического уравнения имеют отрицательные дей­ствительные части, не представляется возможным. Для этого необходимо пользоваться правилом штриховки кривых D-разбиения, Сформулируем это правило применительно к D-разбиению плоскости относительно одно­го параметра или , в следующем виде.

При перемещении вдоль кривой D-разбиения от частоты  до  ее следует штриховать слева, как показано на рисунке 2. Та­ким образом, на плоскости получим несколько зон, отделенных одна от  другой кривой D-разбиения.

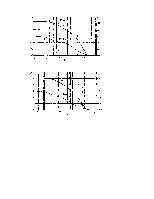
Рассмотрим рисунок 2, а, где показаны три области 1-3. Будем счи­тать, что в зоне 1 каждой точке плоскости соответствует комплексное чис­ло к корней с отрицательной действительной частью. Если при переходе из зоны 1 в зону 2 происходит пересечение кривой D-разбиения с не заштри­хованной стороны на заштрихованную, то в зоне 2 число корней с отрица­тельной действительной частью увеличивается на единицу и отметка точки к становится равной к+ 1. При переходе кривой D-разбиения из зо­ны 1 с заштрихованной стороны на не заштрихованную (зона 3) число корней с отрицательной частью уменьшается на единицу, и отметка точки будет равна к—1.

Интерес представляет исследование только действительных значе­ний параметра w. Поэтому, построив кривые D-разбиения, находят такой отрезок действительной оси на плоскости w(jw), который принадлежит об­ласти устойчивости. Равенство числа отрицательных корней степени ха­рактеристического уравнения позволяет выделить зону, где точки плоско­сти с наибольшим числом соответствуют области устойчивости системы. Числовые значения на действительной оси в этой области определяют принятые параметры или .

Из рисунка 2, а можно установить, что в зоне 2 имеется самая большая отметка точки к + 1, и если она равна п, то в зоне 2 обе­спечивается устойчивость. Числовые значения по оси абсцисс для рас­сматриваемого параметра в области 2 гарантируют устойчивость работы системы. На рисунке 2, б изображена кривая D-разбиения с пятью зонами I-V. В зонах // и Vобеспечивается условие к+1=п и система устойчива. Кривая D-разбиения (рисунок 2, в) выделяет две зоны. В зоне // будет точ­ка с отметкой к +1=п. Она соответствует устойчивости системы. В за­ключение воспользуемся кривыми D-разбиения, приведенными на рисунке 2, г. При этом видно, что наибольшая отметка числа к в зоне /; при к =п зона / является областью устойчивости.

Для удобства вычислений можно брать w = 0 и находить корни ос­тавшегося уравнения. При их числе, равном  с отрицательными действительными частями, имеем k=, а область устойчивости системы будет иметь отметку с точкой  (где =1,2,3,…), равной порядку характеристического уравнения n. Воспользуемся данным положением. Допустим, что кривая D – разбиения, изображенная на рисунке 2, в, построена по характеристическому уравнению вида:

                               (70)

где постоянные коэффициенты.

          Это нетрудно показать, если уравнение (70) можно переписать в виде

                                             (71)

Пусть s=w; тогда выражение (71) будет иметь вид

                                          (72)

Задаваясь в уравнении (72) различными значениями w, построим на рисунке 2, в, кривую D – разбиение.

Рисунок 2. Кривые D – разбиения по одному параметру на пл. w для  определения областей устойчивых и неустойчивых состояний систем:

          а, в, г – с тремя областями; б – с пятью областями.

Теперь положим ; тогда из уравнения (72) получим

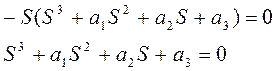                           (73)

откуда  Из уравнения                                                                                                        (73) определим

          Итак, устанавливаем, что один корень имеет нулевое значение, а в трех остальных действительные части отрицательны, т.е. . Так как в зоне 2   k+1=i+, то при i=1  найдем  k+1=4, так как порядок уравнения (73) четвертый. Следовательно, зон 2 соответствует устойчивой системе. При этом ее параметр  изменяется в диапазоне действительных чисел, выделенных на рисунке 2, в, жирной стрелкой.

          Перейдем теперь к рассмотрению САР, в которых можно выделить два параметра  и . Если эти параметры входят в характеристическое уравнение (70) линейно, то его можно переписать в виде:

                                                           (75)

При  из уравнения (75) получим

                        (76)

          Для построения кривой D – разбиения необходимо определить   и  при различных значениях w, решая совместно уравнения:

          В результате из выражений (75) и (76)  найдем два уравнения, в которых можно выделить  и , т.е.

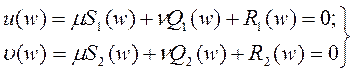                                       (77)

          Из уравнений имеем

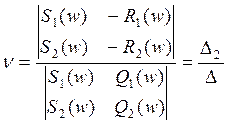
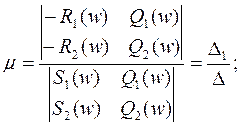
          Пользуясь соотношениями и изменяя w от до  получим в системе координат  кривые D – разбиения.

Сформулируем правило штриховки кривой D-разбиения, постро­енной относительно двух параметров.

При перемещении вдоль кривой D – разбиения от частоты  до  ее следует штриховать слева кривой в тех точках, для которых  и справа при . Отметим, что при изменении со кривая D-разбиения пробегает дважды от w=0 до w=+ и до w=, и ее следует вы­делять двойными штрихами. На рисунке 3, а изображены две различные кривые D-разбиения, которые обозначены цифрами 1 и 2. Из рисунка 3,а видно, что если переход через кривую 2 от точки к происходит с не за­штрихованной стороны на заштрихованную, то число корней с отрица­тельной действительной частью увеличивается на два и отметка точки к становится к + 2. При переходе кривой 1 из зоны с заштрихованной сторо­ны на не заштрихованную число корней с отрицательной действительной частью уменьшается на два и точка отмечается как к— 2.

При движении по кривой D-разбиения в плоскости двух параметров знак  может изменяться только в бесконечности или при частотах w, ко­торым соответствуют особые прямые. В результате этого направление штриховки кривой Д-разбиения меняется только в тех точках, где кривая пересекается с особыми.