Теоретические основы электротехники, страница 4

2.  Составить систему дифференциальных уравнений для метода переменных состояния и рассчитать ток в катушке индуктивности и напряжение на конденсаторе   при   помощи специализированной программы.

3.  Построить временные зависимости в одной системе координат по результатам, полученными двумя методами для:

a.  тока в ветви с индуктивностью

b.  напряжения на конденсаторе

Результаты расчетов занести в таблицу ответов на титульном листе.

 

Решение

Рассмотрим цепь до коммутации (t=0-) и определим начальные условия

 

 

 

В установившемся режиме после коммутации (t→)

 

 

0 A

0 B

Запишем выражение входного сопротивления для послекоммутационной схемы на переменном токе определим корни характеристического уравнения.

 

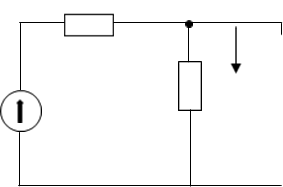                                                                      UL                                   UC                I3

 

 

јω=P

R

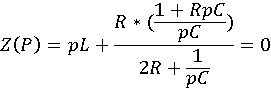
Подставив численные данные и решим относительно p:

16*10^(-4)*p^2+0.28p+20=0

Комплексно-сопряженные корни говорят о периодическом характере переходного процесса. При этом:

Определим напряжение на конденсаторе.

Принужденная составляющая напряжения это установившееся значение напряжения после завершения переходного процесса:

Свободная составляющая это общее решение однородного дифференциального уравнения второго порядка, которое записывается в виде

где - постоянная интегрирования,

Следовательно,

Продифференцируем по времени

Для определения необходимо определить значение искомой функции ее первой производной в начальный период времени. Полагая t=0+ получим два уравнения для определения

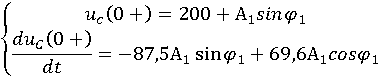
В соответствии с законом коммутации:

Ток в конденсаторе , откуда ;

Запишем уравнения по законам Кирхгофа для начального времени:

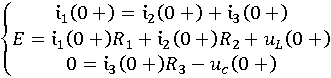
Из третьего уравнения системы:

Подставим в первое уравнение:

 А

Подставим данные значения в систему:

 

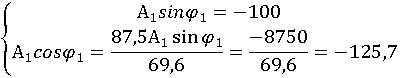
Искомая функция имеет вид

Определим переходной ток через конденсатор:

+

=

Определим ток

Принужденная составляющая и свободная составляющая соответственно равны:

Определим постоянные интегрирования:

В начальный момент времени:

Напряжение на катушке

В соответствии с законом коммутации:

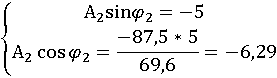
Искомая функция имеет вид

Определим переходное напряжение на катушке индуктивности:

+

-111,36

По первому закону Кирхгофа определим переходной ток

Вывод системы дифференциальных уравнений для метода переменных состояния и расчёт тока в катушке индуктивности и напряжения на конденсаторе   при   помощи специализированной программы.

Выразим из уравнения 1 ток  и подставим в уравнение 3      

Преобразуем и выразим ток

k – Номер шага итерации

k = 0, 1, 2,……. n

Подставив значения в выражение получим:

Для напряжения

 

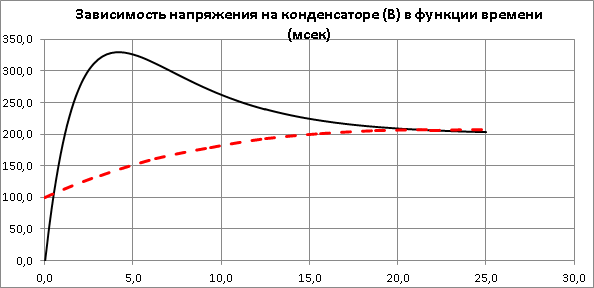
Сведем все результаты в таблицу:

Функция	Вид решения	Значения функции
		при	при	при
=		5	5	10
=		5	5	10
=		0	0	0
=		0	0	0
=		100	100	200