Физика \ Физика

Выбор расчетного напряжения для определения радиальных размеров и допустимых радиальных напряженностей., страница 6

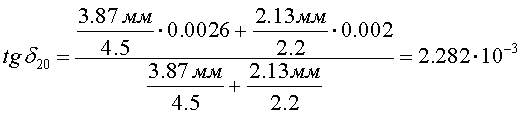
При температуре 90 °С тангенс угла диэлектрических потерь для бумаги и масла , . Тогда тангенс угла диэлектрических потерь комбинированного диэлектрика при 90°С будет равен:

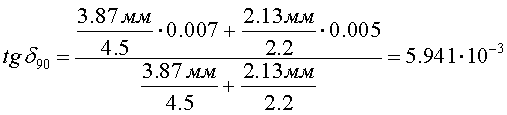
Определим er комбинированного диэлектрика:

.

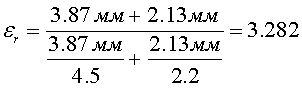Аппроксимируем зависимость tgd = f(T) зависимостью вида tgd = A×exp(B×T). Зная значения tgd и T для двух точек зависимости можно определить коэффициенты A и B: , , тогда:

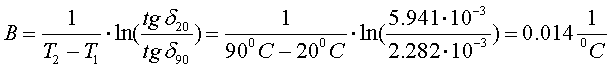
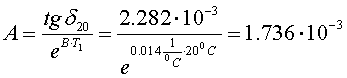
Исходя из полученных данных зависимость примет вид:

Ниже приведен график данной зависимости.

Зависимость тангенса угла диэлектрических потерь от температуры.

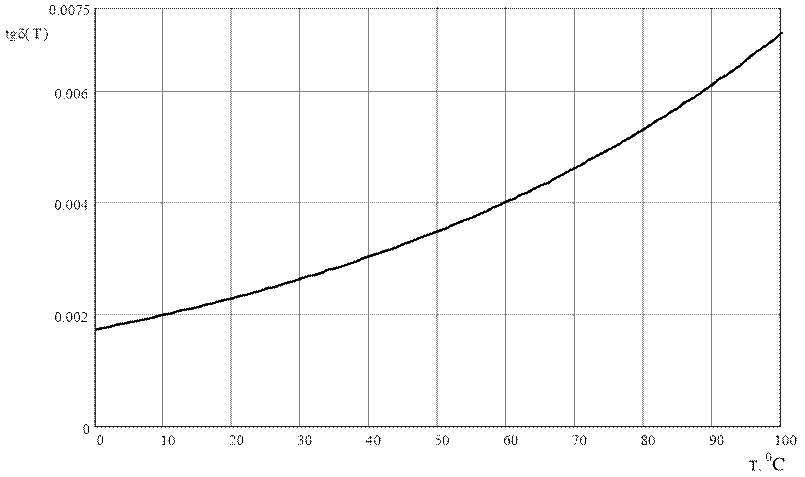
Рис. 7.

Исходными данными для теплового расчёта являются номинальный ток

Iн = 800 А, температура окружающей среды T0 = 35°C, а также результаты электрического расчёта.

На первом шаге задаёмся температурой стержня изолятора Tc = 40 °C. Тогда электрические потери в стержне составят:

1-й слой

Диэлектрические потери в изоляции первого слоя:

где , вместо 44,28 надо 10,4

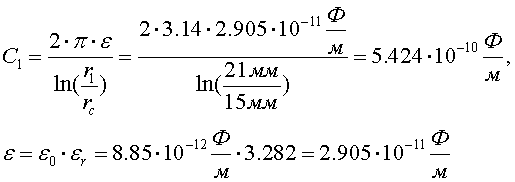
Определим тепловое сопротивление первого слоя на единицу длины при коэффициенте теплопроводности бумажно-масляной изоляции, равном kб = 0.2 Вт/м·оС:

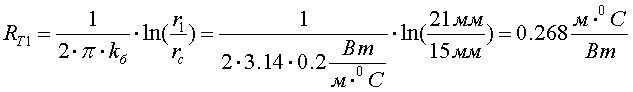
Перепад температуры в первом слое составит:

 

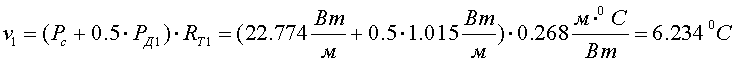
Найдем тепловой поток, проходящий через изоляцию первого слоя:

Температура первой обкладки будет равна:

2-й слой

Диэлектрические потери в изоляции второго слоя:

где

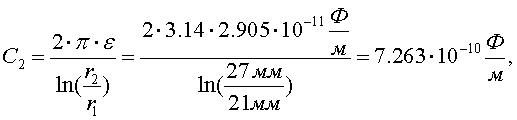
Определим тепловое сопротивление второго слоя на единицу длины при коэффициенте теплопроводности бумажно-масляной изоляции, равном kб = 0.2 Вт/м·оС:

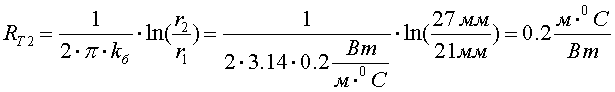
Перепад температуры во втором слое составит:

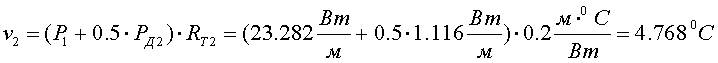
Найдем тепловой поток, проходящий через изоляцию второго слоя:

Температура второй обкладки будет равна:

.

Аналогично расчет ведется для остальных слоев изоляции.

Далее определяем полный тепловой поток Ри, проходящий через бумажно-масляную изоляцию и остальные элементы цилиндрической системы изолятора, а также температуру внешней поверхности изоляции Ти:

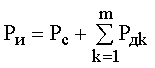
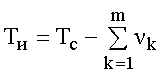
По такой же методике «шаг за шагом» просчитываются аналогичные параметры при Тс = 60, 80 и 100 °С. Результаты теплового расчета сведены в табл. 8.

По полученным данным строится зависимость Ри = f(Ти), а затем зависимость количества тепла, отводимого в единицу времени от наружной поверхности бумажно-масляной изоляции в окружающую среду, от температуры наружной поверхности Ти. Эта зависимость определяется соотношением

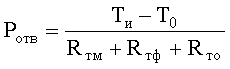, для температуры 40 °С:

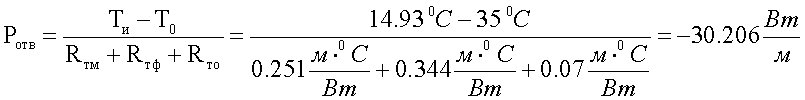
Pотв аналогично рассчитывается для Тс = 40, 60, 80 и 100 °С.

Полученные зависимости приведены на рис. 8.

Таблица 8.

Результаты теплового расчета..

№ слоя

Тепловое

сопротивление

RТк

Погонная

емкость слоя, Ск·10-9 Ф/м

Температура слоя, Тк, 0С

при Тс :

Перепад температуры в слоях, υк, 0С при Тс :

Диэлектрические потери слоя, Рдк, Вт/м при Тс :

40

60

80

100

40

60

80

100

40

60

80

100

1

0.268

0.542

33.766

53.281

72.782

92.246

6.234

6.719

7.218

7.736

1.015

1.343

1.777

2.352

2

0.2

0.726

28.998

48.116

67.197

86.232

4.768

5.165

5.584

6.032

1.116

1.467

1.927

2.532

3

0.16

0.909

25.093

43.863

62.571

81.197

3.905

4.252

4.626

5.034

1.227

1.604

2.095

2.734

4

0.133

1.093

21.754

40.208

58.57

76.812

3.339

3.655

4.001

4.385

1.333

1.734

2.253

2.924

5

0.114

1.275

18.813

36.973

55.008

72.881

2.941

3.235

3.562

3.931

1.413

1.83

2.367

3.055

6

0.1

1.458

16.162

34.042

51.763

69.277

2.65

2.93

3.245

3.604

1.568

2.022

2.602

3.342

7

0.045

3.193

14.93

32.676

50.246

67.585

1.232

1.366

1.518

1.692

0.954

1.225

1.57

2.007
Скачать файл