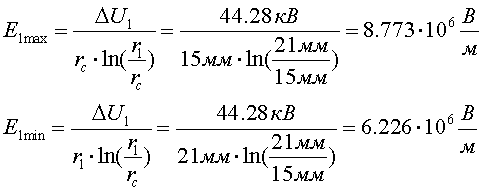
Остальные величины напряженностей слоев приведены в табл. 7.
Таблица 7.
Напряженности слоев.
|
Номер слоя, m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Максимальная напряженность, Ek max·106, В/м |
8.773 |
7.941 |
7.493 |
7.198 |
6.936 |
6.91 |
7.17 |
|
Минимальная напряженность, Ek min·106, В/м |
6.266 |
6.177 |
6.131 |
6.091 |
6.011 |
6.097 |
6.771 |
По полученным данным строим график распределения радиальных напряженностей по слоям, по оси абсцисс которого откладывается радиус слоя, а по оси ординат – значение напряженности, соответствующей этому радиусу.
График распределения радиальных напряженностей.
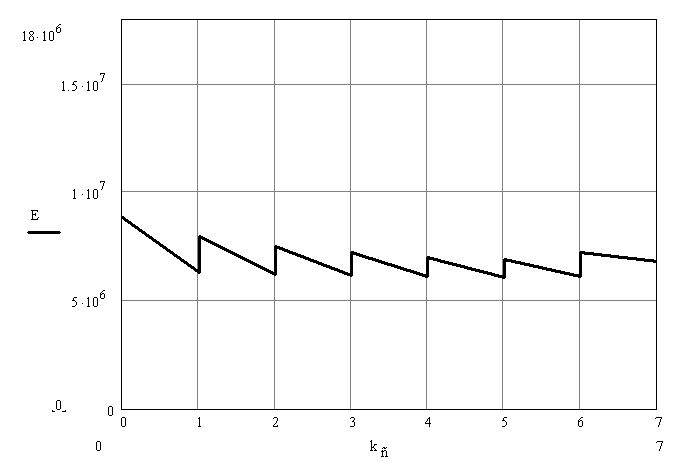
Рис. 5.
Из расчета видно, что напряженность в каждом слое не превышает допустимое значение 18 кВ/мм, это говорит о том, что электрический расчет выполнен верно.
При расчёте тепловой устойчивости проходного изолятора выясняется возможность развития теплового пробоя в проектируемой конструкции при заданном токе, проходящем по токоведущему стержню, и наибольшем допустимом напряжении.
Так как аксиальные размеры изолятора существенно больше радиальных, при проведении теплового расчёта принимают, что тепловое поле изолятора радиально, т.е. вся теплоотдача осуществляется только в радиальном направлении (рис. 3.1).
Схема для графического расчёта тепловой устойчивости
изолятора конденсаторного типа
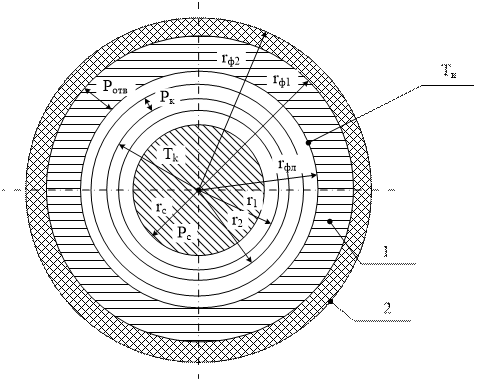
1 – масло, 2 – фарфор.
Рис. 6.
Расчёт выполняется для установившегося теплового режима изоляции. Исходными данными при расчёте являются ток в стержне изолятора, температура окружающей среды и зависимость tgd от температуры для применяемой изоляции.
Расчёт производится методом «шаг за шагом». Для проведения расчёта задаются рядом значений температуры стержня Тс1, Тс2, …, Тсn. Эти значения произвольны, но должны быть близки к возможной искомой температуре стержня Тс при данных условиях. Практически для изоляторов высокого напряжения удобно принять значения Тс равными 40, 60, 80 и 100 °С.
Найдем тепловые сопротивления масляного зазора, фарфоровой покрышки, окружающей среды. Тепловое сопротивление масляного зазора:
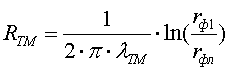
где ![]() -
коэффициент теплопроводности масла.
-
коэффициент теплопроводности масла.
Принимаем толщину зазора Δз = 20 мм, а толщину фарфоровой стенки изолятора – Δф = 40 мм, тогда:
![]()
![]()
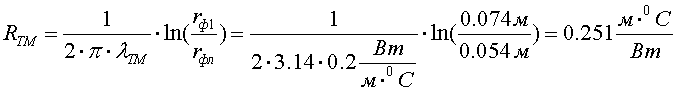
Тепловое сопротивление фарфоровой покрышки:
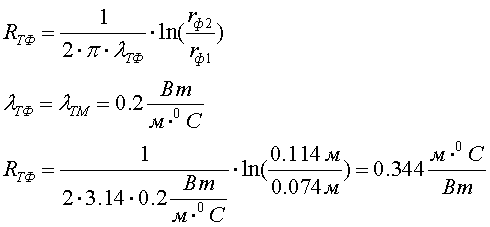
Для расчёта теплоотдачи ввода в окружающую среду принимается коэффициент теплоотдачи с поверхности фарфора kтв = 20 Вт/(м2 ×°С), тогда:
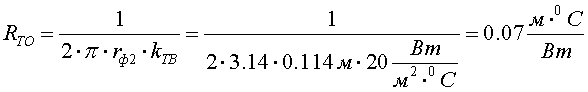
Определим полный тепловой поток изолятора и соответствующей ему температуры внешней поверхности изолятора. Найдем потери в токоведущем стержне:
![]() ,
где
,
где
![]() -
температурный коэффициент сопротивления медного стержня;
-
температурный коэффициент сопротивления медного стержня;
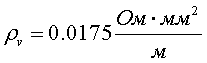 -
удельное объемное сопротивление медного стержня;
-
удельное объемное сопротивление медного стержня;
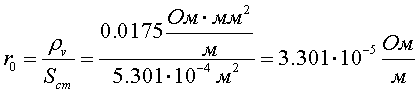 -
активное сопротивление стержня;
-
активное сопротивление стержня;
![]() -
сечение стержня.
-
сечение стержня.
Для теплового расчета изолятора требуется значение tg δ в диапазоне температур от 40 до 100 оС. Для данного ввода применяется масло ГК и кабельная бумага КВМСУ 120. Произведем аппроксимацию зависимости
tg δ = f(T) зависимостью вида: tg δ = A·exp(B·T).
Определим тангенс угла диэлектрических потерь комбинированной изоляции.
Для бумажно-масляной изоляции tg δ и εr рассчитываются по формулам:
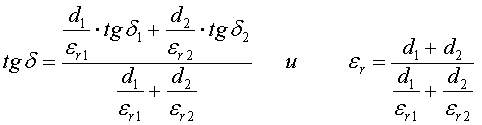 ,
,
![]() –
соответственно толщина, относительная диэлектрическая проницаемость и тангенс
угла диэлектрических потерь бумаги;
–
соответственно толщина, относительная диэлектрическая проницаемость и тангенс
угла диэлектрических потерь бумаги;
![]() –
соответственно толщина, относительная диэлектрическая проницаемость и тангенс
угла диэлектрических потерь масла.
–
соответственно толщина, относительная диэлектрическая проницаемость и тангенс
угла диэлектрических потерь масла.
Для бумаги и масла можно принять er1 = 4.5, er2 = 2.2.
Предполагая, что бумага пористая и все поры бумаги заполнены пропитывающим составом, имеем:
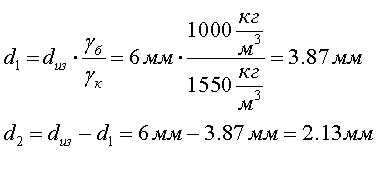
где gб, gк – плотность бумаги и клетчатки соответственно, dиз – полная толщина изоляции.
При температуре 20°С тангенс угла
диэлектрических потерь для бумаги (индекс 1) и масла (индекс 2) равны
соответственно ![]() и
и
![]() ,
тогда тангенс угла диэлектрических потерь комбинированного диэлектрика при 20°С будет равен:
,
тогда тангенс угла диэлектрических потерь комбинированного диэлектрика при 20°С будет равен:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.