Анализ устойчивости системы по критериям устойчивости Гурвица и Найквиста, страница 2

Критерий Найквиста позволяет по годографу амплитудной фазовой характеристики системы судить об устойчивости замкнутой системы. Годограф имеет действительную  и мнимую оси, на которых откладываются соответственно действительные и мнимые значения передаточной функции  в зависимости от частоты. Критерий Найквиста можно сформулировать следующим образом: САР, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если годограф не охватывает точку (-1, j0). В противном случае, при неустойчивости системы, годограф охватывает эту точку в положительном направлении  раз, где p – количество корней.

Для этого в выражении для Wобщ(p) заменим p на jw.

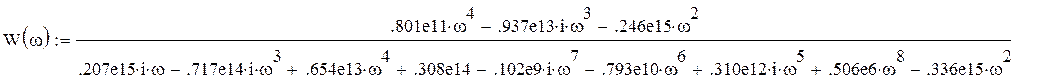
Определим действительную U(w)  и мнимую части V(w) передаточной функции. Для этого необходимо умножить  числитель и знаменатель выражения W(w) на сопряженное знаменателю выражение. В итоге получим выражение:

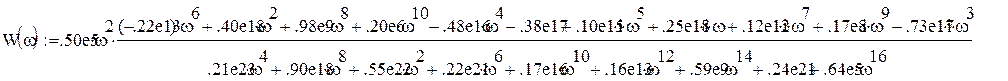
Выражения для действительной и мнимой частей соответственно:

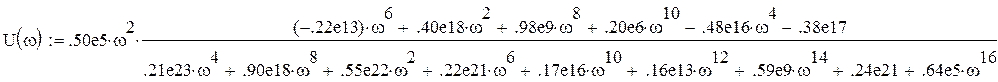
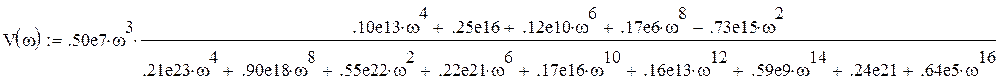
Построим зависимость V(w)  от U(w), чтобы определить устойчивость системы.

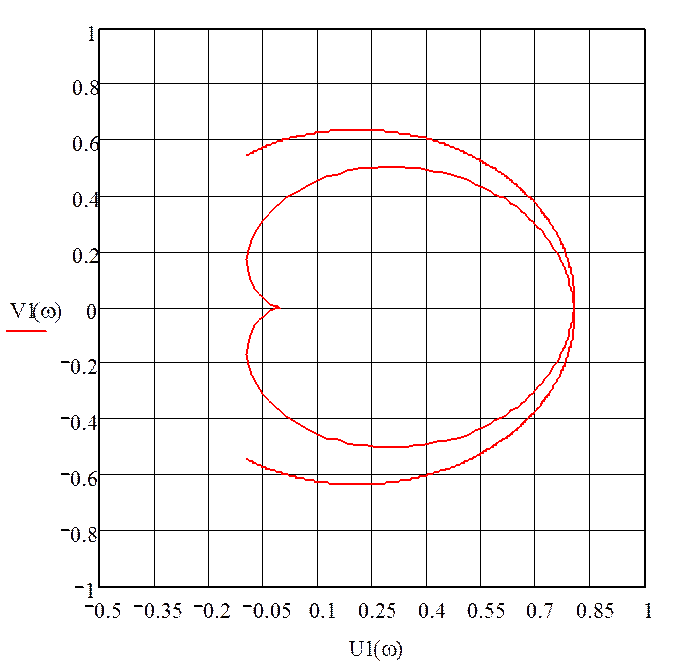
Рисунок – Годограф ………

На графике видно, что годограф не охватывает точку (-1;j0). Это означает, что система устойчивая.

1.6  Построение переходного процесса.

Он определяется как  обратное преобразование Лапласа от W(p)/p. Тогда получим

                                                                      

                        

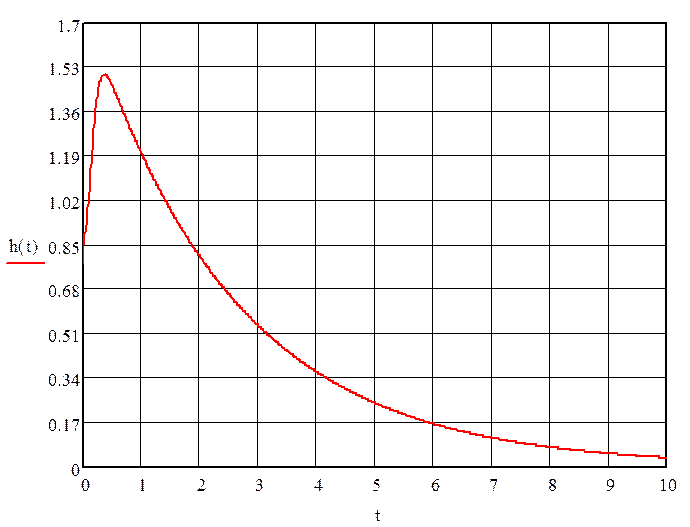
                   Рисунок – График переходного процесса системы

По графику переходного процесса определим все характеристики системы.

h_max=1,53        h_уст=0        t_max=0,3         t_p=8,4       t_согл=9,5

Перерегулирование равно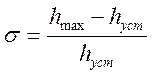. Так как h_уст=0 , то определить перерегулирование для данной системы не допустимо.

6) Построим амплитудно-частотную характеристику.

АЧХ определяется по выражению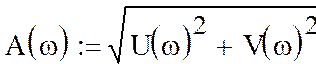 

Подставив ранее рассчитанные выражения для U(w) и V(w), получим

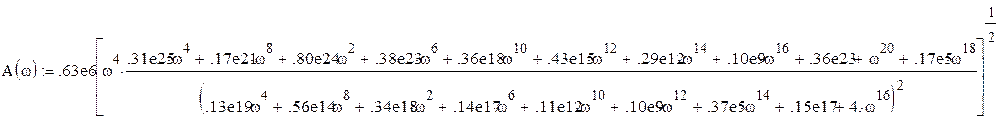
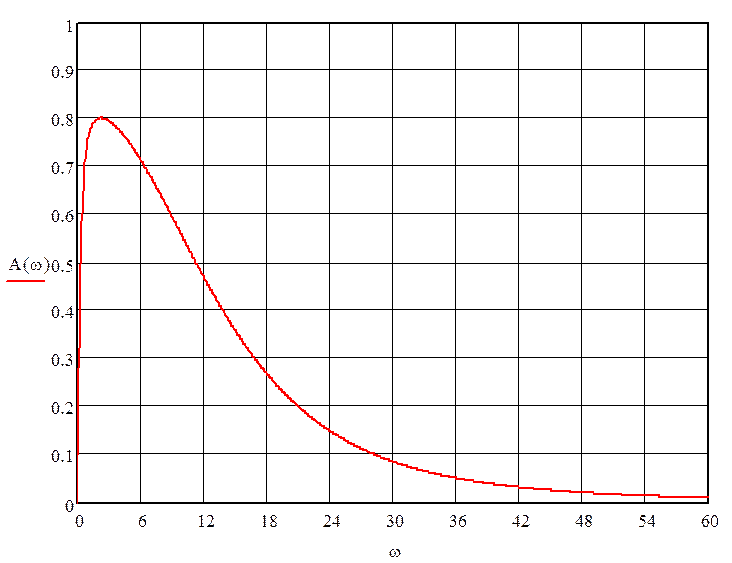
Рисунок – График амплитудно-частотной характеристики системы

По графику определим следующие характеристики:

 Amax=0,55       A(0)=0      A=0,7Amax=0,38    

Полоса пропускания сигнала  равна    (  ),

 то есть равна 11,72.

Показатель колебательности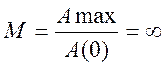

Вывод по линейной части:

Проведя анализ устойчивости системы по критериям устойчивости Гурвица и Найквиста, было определено, что данная система очистки сточных вод в аэротенках устойчивая, так как……… По графику переходной функции видно, что быстродействие системы равно 8,4 с. По графику амплитудно-частотной функции видно, что полоса пропускания сигнала равна 11,72.

2 ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ ЧАСТИ СИСТЕМЫ

2.1 Упрощение структурной схемы системы с нелинейным элементом

Структурная схема с нелинейным элементом имеет вид:

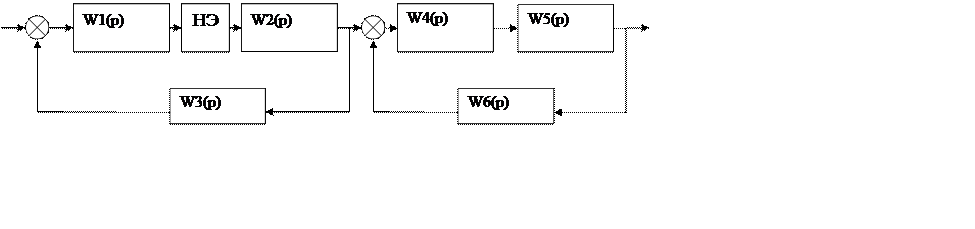
Рисунок – Структурная схема с нелинейным элементом

В данной схеме:

                                         

                                           

y

График, описывающий нелинейный элемент НЭ, приведен на рисунке

2

                                                                     

        

x

                                                                 

-2

                                      

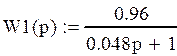
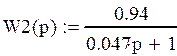
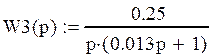
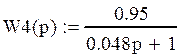
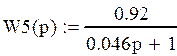
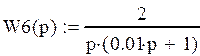
Рисунок  -  Характеристика нелинейного элемента

Упростим правую часть структурной схемы.

В этой схеме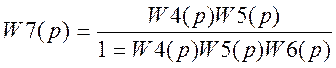           

Внесем звено W₇(p) в цепь ООС и получим :

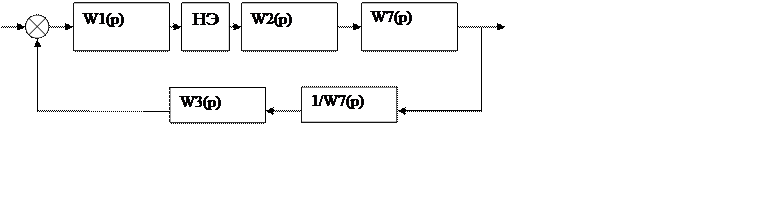
Разорвем цепь перед нелинейным элементом и получим

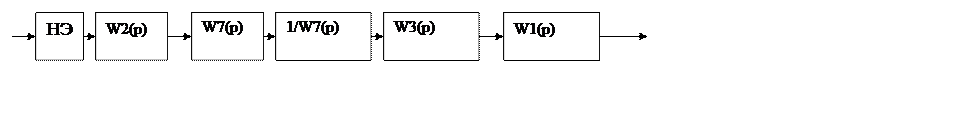
В  этой цепи можно четко выделить линейную и нелинейную части, введя замену:      .Тогда преобразованная структурная схема примет вид:

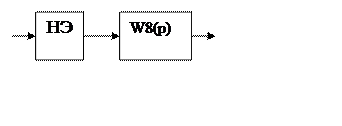
Насильственно замкнем данную цепь единичной ООС :

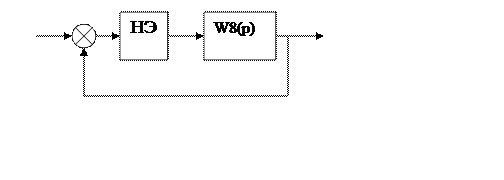
Запишем общую передаточную функцию линейной части:

Подставляя значения передаточных функций звеньев, получим:

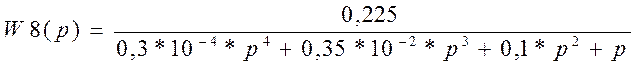
2.2  Построение фазового портрета

Передаточную функцию можно записать в виде 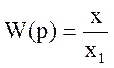 или , подставляя в эту формулу значение передаточной функции, получим:

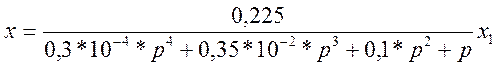
Приведенную формулу можно записать в виде:

Воспользуемся пакетом MathCad для решения этого дифференциального уравнения. Введем замену pⁱx=y_i и исключим из левой части уравнения производные выше второго полрядка. Получим систему уравнений для участков (-∞;0) и (0;+∞):

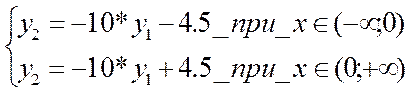
Создадим матрицу для решения дифференциального уравнения:

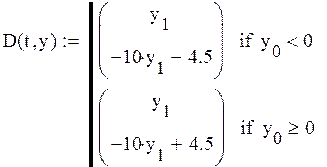
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:

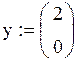
Возьмем количество точек равным 10000 и конечное время интегрирования 100, то матрица решений запишется как: .

По введенным данным получим фазовый портрет (рисунок).

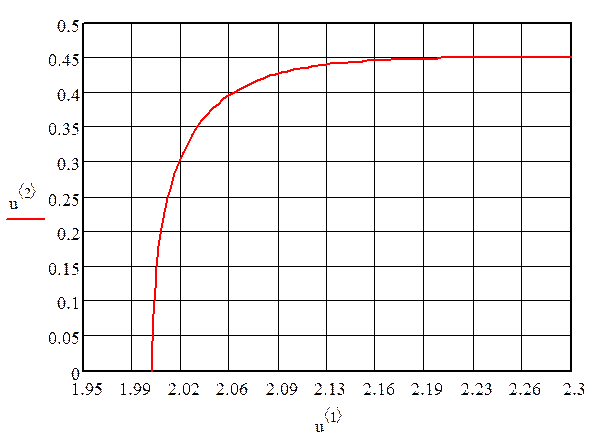
Рисунок -   

4 Анализ устойчивости

На рисунке 9 представлен фазовый портрет нелинейной системы. Это типовой вид кривой. До перехода через точку -2 работает первое уравнение системы, при переходе через эту точку начинает работать второе уравнение. Третье уравнение работает при переходе через точку 2. Характер фазовой линии такой, что она постоянно приближается к началу координат, т.е. нелинейная система с релейным элементом устойчива. При движении к состоянию устойчивости амплитуда колебаний постоянно уменьшается, а частота переключения растет. Получаем, что амплитуда колебаний в итоге примет нулевое значение, а частота колебаний станет бесконечно большой.