2.Расчет рычажного механизма.
2.1 Исходные данные для расчета рычажного механизма.
 |
Таблица 1. Исходные данные для проектирования рычажного механизма.
Параметр |
LBD |
LBC |
LOA |
LAB |
m2 |
m3 |
m4 |
m5 |
Jо1=Js3 |
Js2 |
Js4 |
Jдв |
FC1 |
|
|
Размерность |
м |
м |
м |
м |
кг |
кг |
кг |
кг |
кг м2 |
кг м2 |
кг м2 |
кг м2 |
кН |
Град |
Величина |
1,5 |
0,4 |
0,1 |
0,45 |
18 |
20 |
95 |
450 |
1 |
0,04 |
42 |
0,26 |
1,5 |
210 |
2.2 Структурный анализ рычажного механизма.
B
 |
![]() 4
4
![]()
![]() 2 3
2 3
5
 |
|||
O 1 C
![]()
![]()
![]()
![]()
![]()
![]() D 6
D 6
A
Рис. 2. Схема рычажного механизма
Таблица 2. Звенья рычажного механизма
|
Номер |
Название |
Вид движения |
Особенности движения |
|
1 2 3 4 5 6 |
Кривошип Шатун ШатунШатунПолзун Стойка |
Вращательное Плоскопараллельное Плоскопараллельное Плоскопараллельное Возвратно-поступательноеОтсутствует |
Полный оборот |
Таблица 3. Кинематические пары. Звенья рычажного механизма.
|
Обозначение |
Звенья пары |
Название |
Класс |
О |
6-1 |
Вращательная |
5 |
|
А |
1-2 |
Вращательная |
5 |
|
В |
2-3 |
Вращательная |
5 |
|
B
|
3-4 6-3 |
Вращательная Вращательная |
5 5 |
|
D |
4-5 |
Вращательная |
5 |
|
D |
5-6 |
Поступательная |
5 |
Степень подвижности механизма определяется по формуле Чебышева
W = 3*n – 2*p5 - p4, где:
W - число степеней подвижности механизма;
N=5 - число подвижных звеньев ;
р5=7 - число низших кинематических пар (пятого класса);
р4=0 - число высших кинематических пар (четвертого класса);
W=3*5-2*7=1.
Звено 1 примем за входное. Разделим кинематическую схему механизма на начальное звено (рис. 3,а) и структурные группы (рис. 3 б,в).
![]()
![]()

![]()
![]() 2 4
2 4
![]()
![]()
![]() 1 5
1 5
![]()
![]() 3
3
Рис. 3 а Механизм 1-го класса Рис. 3 б,в Гр. Ассура 2-го класса,
2-го порядка
2.3 Кинематический анализ рычажного механизма.
Рабочий ход механизма осуществляется тогда, когда ползун движется влево.
Данные, необходимые для расчета кинематических диаграмм,планов скоростей, ускорений и силового расчета: n1 = 63 об/мин .
2.3.1 Кинематические диаграммы движения ползуна.
Диаграмму перемещений строим, замеряя соответствующие перемещения ползуна и откладывая их вдоль оси перемещений:
![]() S= 4,8/103=0.047
S= 4,8/103=0.047 ![]() ;
; ![]() t=2p/w=2*3,14/6,6=0.95
t=2p/w=2*3,14/6,6=0.95
![]() .
.
Для построения
диаграммы скоростей используем метод графического дифференцирования (метод
хорд). Диаграмма скоростей выполняется в масштабе ![]() v , равном:
v , равном:
mv=ms/H*mt=0,047/22*0,95=0,0022 (м/с)/мм.
Для построения
диаграммы ускорений продифференцируем графически диаграмму перемещений.
Диаграмма ускорений выполняется в масштабе ![]() а.:
а.:
ma=mv/H*mt=0,0022/22*0,95=0,001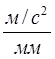 .
.
2.3.2 Планы скоростей.
План скоростей строится для определения графическим методом скоростей характерных точек звеньев механизма.
План скоростей
выполняется в масштабе ![]() v.
v.
![]() v =
v = ![]() ;
;
Рассмотрим группу Ассура 2 – 3 (АВ). Она присоединена с помощью
шарниров к точкам А и В. Величина скорости точки А определяется по формуле : V
a =![]() 1*lOA,
1*lOA,
где ![]() 1
-угловая скорость первого звена, рассчитывается по формуле :v1=
1
-угловая скорость первого звена, рассчитывается по формуле :v1=![]() *n1/30=3.14*63/30=6.6 c-1,где n1-
частота вращения первого звена.
*n1/30=3.14*63/30=6.6 c-1,где n1-
частота вращения первого звена.
Определим величину скорости точки А:
V a = 6.6*0,1 = 0.66 м/с .
![]()
![]()
![]() Построение плана скоростей
выполняем в соответствии с системой уравнений:
Построение плана скоростей
выполняем в соответствии с системой уравнений:
![]()
![]()
![]() {VB = VA + VBA
{VB = VA + VBA
![]()
![]() {VB = VC + VBC (VC=0) ;
{VB = VC + VBC (VC=0) ;
![]()
![]()
![]() {VD = VB + VDB
{VD = VB + VDB
{VD = VD6 + VDD6 .
Масштабный коэффициент плана скоростей будет:
![]()
![]() v=
v= 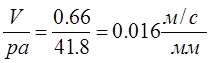 .
.
Определим угловые скорости звеньев. Угловая скорость звена 1 ![]() 1
былаопределена выше. Она направлена по часовой стрелке и равна
6.6 с-1 .Угловые скорости остальных звеньев найдем по формулам:
1
былаопределена выше. Она направлена по часовой стрелке и равна
6.6 с-1 .Угловые скорости остальных звеньев найдем по формулам:
![]() =VBA/lAB=ab*
=VBA/lAB=ab*![]() v/lAB=32*0.016/0.45=1.14 с-1;
v/lAB=32*0.016/0.45=1.14 с-1;
![]() = VB/lBC=pb*0.016/lAB=62.5*0.016/0.4=2.50
c-1;
= VB/lBC=pb*0.016/lAB=62.5*0.016/0.4=2.50
c-1;
![]() = VDB/lBD=bd*0.016/1.5=34*0.016/1.5=0.36 c-1.
= VDB/lBD=bd*0.016/1.5=34*0.016/1.5=0.36 c-1.
2.3.3 Планы ускорений.
План ускорений строится для определения
графическим методом ускорений характерных точек звеньев механизма. План
ускорений строится в масштабе![]() a.
Масштабный коэффициент находится аналогично масштабному коэффициенту плана
скоростей.
a.
Масштабный коэффициент находится аналогично масштабному коэффициенту плана
скоростей.
Полное ускорение звеньев механизма складывается из нормальной и тангенциальной составляющей и находится по формуле:
а = ![]() ;
;
aA=anA=![]() 12*lOA=6.62*0.1=4.356
м/c2.
12*lOA=6.62*0.1=4.356
м/c2.
![]()
![]()
![]()
![]() Построение плана ускорений
выполняем в соответствии с системами уравнений. Для определения ускорения точки
B напишем два векторных уравнения:
Построение плана ускорений
выполняем в соответствии с системами уравнений. Для определения ускорения точки
B напишем два векторных уравнения:
![]()
![]()
![]()
![]()
![]() {aB = aA
+ anBA + atBA
{aB = aA
+ anBA + atBA
{aB = aC + anBC + atBC (aC=0);
Определим нормальные ускорения anBA и anBC:
anBA=![]() 22*lAB=1.142*0.45=0.58 м/c2;
22*lAB=1.142*0.45=0.58 м/c2;
anBC=![]() 32*lBC=2.52*0.4=2.5 м/c2.
32*lBC=2.52*0.4=2.5 м/c2.
Рассмотрим следующие два уравнения для определения ускорения точки D:
![]()
![]()
![]()
![]() {aD = aB + anBD
+ atBD
{aD = aB + anBD
+ atBD
![]()
![]()
![]()
![]()
![]()
![]() {aD = aD6 + akDD6
+ atDD6 (aD6=0, akDD6=0)
.
{aD = aD6 + akDD6
+ atDD6 (aD6=0, akDD6=0)
.
Найдем нормальное ускорение an BD:
an BD=![]() 42*lBD=0.362*1.5=0.19 м/c2.
42*lBD=0.362*1.5=0.19 м/c2.
Масштабный коэффициент плана ускорений будет:
![]()
![]() a=aA/
a=aA/![]() a=4.356/87.12=0.05
a=4.356/87.12=0.05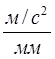 .
.
Определим длину отрезков на плане ускорений:
an1=anBA/![]() a=0.585/0.05=11.7 мм;
a=0.585/0.05=11.7 мм;
![]() n2=anBC/
n2=anBC/![]() a =2.5/0.05 =50 мм;
a =2.5/0.05 =50 мм;
bn3=anDB/![]() a =0.1944/0.05=3.88 мм .
a =0.1944/0.05=3.88 мм .
Ведущее
звено 1 вращается с постоянной скоростью, поэтому его угловое ускорение ![]() 1=0. Найдем угловые ускорения
остальных звеньев:
1=0. Найдем угловые ускорения
остальных звеньев:![]()
![]() =
= ![]() = 194*0.05/0.45=21.56
c-2;
= 194*0.05/0.45=21.56
c-2;
![]() =atBC/lBC=103.5*0.05/0.4= 12.94 с-2;
=atBC/lBC=103.5*0.05/0.4= 12.94 с-2;
![]() =atDB/lDB=8.5*0.05/1.5= 0.28 с-2.
=atDB/lDB=8.5*0.05/1.5= 0.28 с-2.
2.4 Силовой расчет механизма.
![]() Целью силового расчета
является определение реакций в кинематических парах. Силовой расчет выполнен по
принципу Даламбера, cогласно которому к звеньям механизма условно
прикладываются силы инерции звеньев, моменты сил инерции, и все внешние силы.
Считаем динамическую систему статической, т.е. неподвижной и составляем
уравнения кинетостатики используя аксиомы и теории статики в том числе условия
равновесия сил: сумма всех сил действующих на звено равна нулю. Силовой расчет
начинаем со структурной группы 4-5. Структурные группы изображаем в
соответствии с масштабным коэффициентом ml=lBD/BD =1.5/150=0.01м/мм.
Целью силового расчета
является определение реакций в кинематических парах. Силовой расчет выполнен по
принципу Даламбера, cогласно которому к звеньям механизма условно
прикладываются силы инерции звеньев, моменты сил инерции, и все внешние силы.
Считаем динамическую систему статической, т.е. неподвижной и составляем
уравнения кинетостатики используя аксиомы и теории статики в том числе условия
равновесия сил: сумма всех сил действующих на звено равна нулю. Силовой расчет
начинаем со структурной группы 4-5. Структурные группы изображаем в
соответствии с масштабным коэффициентом ml=lBD/BD =1.5/150=0.01м/мм.
Определяем силы инерции, моменты инерции по формулам:
G4=m4*g=931 H; G5=m5*g=4410 H;
![]() Fи5= m5*as5 = m5*
Fи5= m5*as5 = m5*![]() d*
d*![]() a=450*109*0.05=2452.5 H;
a=450*109*0.05=2452.5 H;
Mи5 =0 ;
![]() Fи4= m4*as4 = m4*
Fи4= m4*as4 = m4*![]() s4*
s4*![]() a=95*112.5*0.05=534.4 H;
a=95*112.5*0.05=534.4 H;
![]()
![]() Mи4 = - Js4*
Mи4 = - Js4*![]() =-42*0.28=-11.76 Н*м .
=-42*0.28=-11.76 Н*м .
Составляем векторную сумму сил и сумму моментов относительно точки D:
![]() MD
= 0;
MD
= 0;
Fи4*hFи4+
Ft3,4*LBD+ G4*hG4+
Mи4*1/![]() L=0;
L=0;
hFи4=22мм; LBD=150мм; hG4=72мм .
Выразим из уравнения Ft3,4:
Ft3,4=(-534.4*22-931*72-11.76/0.01)/150=-533 H.
Масштабный коэффициент будет равен:
![]() F=500/10=50
Н/мм. Отсюда найдем F45 и F34:
F=500/10=50
Н/мм. Отсюда найдем F45 и F34:
![]() F45=F45*
F45=F45*![]() F=125*50=6250
H;
F=125*50=6250
H;
![]()
![]() F34= F34*
F34= F34*![]() F=
35*50=1750 H
F=
35*50=1750 H
Определим моменты инерции и силы инерции второго и третьего звена:
G3 = 196 H;
G2 = 176.4 H;
![]()
![]() Mи2 = - Js2*
Mи2 = - Js2*![]() = -0.04*21.56=-0.8624 Н*м;
= -0.04*21.56=-0.8624 Н*м;
![]() Fи2 = m2*as2 = m2*
Fи2 = m2*as2 = m2*![]() s2*
s2*![]() a=18*32*0.05=28.8 H;
a=18*32*0.05=28.8 H;
![]() Mи3=-Js3*
Mи3=-Js3*![]() =-1*12.94=-12.94 H*м;
=-1*12.94=-12.94 H*м;
Fи3 = m3*as3 = m3*![]() b*
b*![]() a=20*115*0.05=115 H .
a=20*115*0.05=115 H .
Составляем векторную сумму сил и сумму моментов относительно точки В:
![]() MB(2) =
0;
MB(2) =
0;
Ft1,2*hF1,2 +
Mи2*1/![]() L + G2*hG2 - Fи2*hFи2 =
0.
L + G2*hG2 - Fи2*hFи2 =
0.
Выразим из уравнения Ft1,2:
Ft1,2*45=Fи2*12- G2*3- Mи2/0.01;
Ft1,2=(28.8*12-176*3-86.24)/45=-6 H;
![]() MB(3) = 0;
MB(3) = 0;
Ft2,3* hF2,3- G3*hG3-
Fи3*hFи3+ Mи3*1/![]() L=0.
L=0.
Выразим из уравнения Ft2,3:
Ft2,3=(196*10+115*18-1294)/40=68.4 H
Масштабный коэффициент будет равен:
![]() F=3
Н/мм , отсюда
F=3
Н/мм , отсюда
![]() F1,2=F1,2*
F1,2=F1,2*![]() F=1780.88
H;
F=1780.88
H;
![]() F2,3=F2,3*
F2,3=F2,3*![]() F=2653.6
H.
F=2653.6
H.
Составляем векторную сумму сил и сумму моментов относительно точки O:
![]() MO
= 0;
MO
= 0;
Mур-F2,1*hF2,1*![]() L=0.
L=0.
Из этого уравнения определяем уравновешивающий момент:
Mур= F2,1*hF2,1*![]() L=480*21*0.01=100.8
Н*м.
L=480*21*0.01=100.8
Н*м.
Уравновешивающий момент является тормозящей нагрузкой, т.к. он направлен в сторону, противоположную направлению угловой скорости.
Теперь определяем мощность двигателя, учитывая что частота вращения
ω1 = 6.6 c-1
Pдв = 9968.1*6.6= 65.8 кВт.
3.Расчет зубчатого механизма.
3.1 Исходные данные для расчета зубчатого механизма.
 |
![]()
![]()
![]()
![]()
![]() a
a
![]()
![]() nДВ
nДВ
 |
 |
||
![]()
![]()
![]()
![]()
![]()
![]()
![]() m
m
![]()
![]() m1
m1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() nP
nP
![]()
![]() b
b
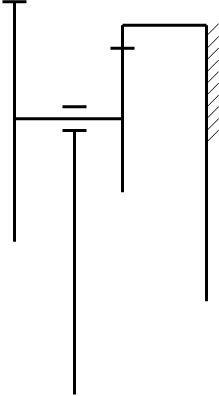
Рис.4.Схема зубчатого механизма
Таблица 4. Исходные данные для проектирования зубчатого механизма.
Параметр |
nдв |
nр |
m1 |
Za |
Zb |
m |
|
Размерность |
об/мин |
об/мин |
мм |
- |
- |
мм |
Величина |
1260 |
63 |
4 |
14 |
45 |
7 |
3.2 Расчет зубчатой передачи.
Зубчатый механизм предназначен для понижения угловой скорости вала и увеличения крутящего момента.
Вычислим окружной шаг по делительной окружности и угловой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.