Определение основных параметров эвольвентных зубчатых колёс.
4. Геометрический синтез и кинематический анализ зубчатого механизма.
5. Литература
Дата выдачи задания_________________________________________________
Срок выполнения____________________________________________________
Руководитель_______________________________________________________
ОГЛАВЛЕНИЕ
1) Цели и задачи курсового проекта
2) Исследование рычажного механизма а) Структурное исследование б) Кинематическое исследование в) Построение плана скоростей при холостом ходе г) Построение плана скоростей при рабочем ходе д) Определение угловых скоростей е) Построение плана ускорений при холостом ходе ж) Построение плана ускорений при рабочем ходе з) Определение угловых ускорений и) Построение кинематических диаграмм к) Силовой анализ л) Построение рычага Жуковского
3) Проектирование зубчатой передачи и эпициклического механизма а) Исходные данные для расчёта эпициклического механизма б) Расчёт параметров корригированных зубчатых колёс в) Геометрический синтез планетарного механизма г) Графический метод кинематического анализа механизма д) Построение эвольвенты
4) Литература
Цели и задачи курсового проекта
Курсовой проект состоит из нескольких разделов, в которых проведено исследование и проектирование машины, состоящей из двигателя, зубчатого механизма, кулачкового механизма и стержневого механизма
1. Исследование стержневого механизма включает кинематический и силовой анализ (структура механизма планы скоростей и ускорений, планы сил, рычаг Жуковского).
2. Исследование зубчатого механизма включает геометрический синтез эвольвентного зацепления и эпициклического механизма, а также кинематическое исследование зубчатого механизма.
Исследование рычажного механизма
Структурное исследование
Степень подвижности механизма определяется по формуле Чебышева W=3n-2p5-p4, где n-число подвижных звеньев; Р5 - числе низших кинематических пар (пятого класса); Р4- число высших кинематических пар (четвертого класса ) В рассматриваемом шестизвенном механизме число подвижных звеньев n=5. В числе низших кинематических пар имеем 6 вращательных (шарниров) - в точках O, A1, A2, В, С, D и одну кинематическую пару, соединяющую ползун 5 с неподвижной направляющей (стойкой). Следовательно Р5=7. Кинематических пар четвертого класса в данном механизме нет, т.е. Р4=0. Подставляя эти значения в формулу получим
W =3*5 -2*7 =1.
Исходные данные для исследования рычажного механизма
|
Параметр |
|
|
|
|
m3 |
m4 |
m5 |
Js2 |
Js4 |
Fрез |
|
|
|
Размерность |
м |
м |
м |
м |
кг |
кг |
кг |
кг м2 |
кг м2 |
кН |
Град |
|
|
Величина |
0,12 |
0,04 |
0,08 |
1,6 |
22 |
6 |
34 |
0,25 |
0,07 |
1,5 |
150 |
|
Таблица звеньев
|
№n/n |
Наименование звеньев |
|
0 |
Стойка |
|
1 |
Кривошип |
|
2 |
Камень |
|
3 |
Кулиса |
|
4 |
Шатун |
|
5 |
Ползун |
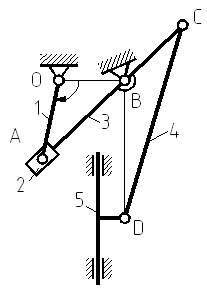
Схема рычажного механизма
Таблица кинематических пар
|
Обозначение КП |
Звенья, входящие в КП |
Наименование КП |
Класс КП |
|
0 |
0-1 |
Вращательная |
5 |
|
А1 |
1-2 |
Вращательная |
5 |
|
А2 |
2-3 |
Поступательная |
5 |
|
В |
0-3 |
Вращательная |
5 |
|
С |
3-4 |
Вращательная |
5 |
|
D1 |
4-5 |
Вращательная |
5 |
|
D2 |
5-0 |
Поступательная |
5 |
Разложение механизма на группы Ассура


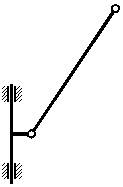
Механизм 1-гокласса. Группы Ассура 2-го класса, 2-го порядка
Формула строения механизма: (0;1)=>(2;3)=>(4;5)
Кинематический анализ рычажного механизма.
Выбираем
масштабный коэффициент длины для построения плана положений. Масштабный
коэффициент длины определяется из выражения ![]() =
=
![]() , где l -
истинная длина;
, где l -
истинная длина; ![]() - масштабная
длина звена на чертеже.
- масштабная
длина звена на чертеже.
![]()
Планы скоростей.
Холостой ход.
Согласно формуле строения механизма план скоростей (ускорений) строим в такой последовательности: механизм первого класса (0,1), группа (2,3), группа (4,5).
Для механизма первого класса определяем скорость центра шарнира A1.
![]() , где
, где ![]() , поэтому
, поэтому
![]() .
.
Выбираем на плоскости произвольную точку Р – полюс плана скоростей. Полюс Pявляется началом плана скоростей. Изобразим скорость VAотрезком
pа1, равным по величине 100 мм. Считаем величину масштаба скоростей:
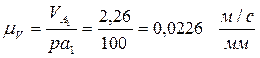
Отрезок ра1 направлен перпендикулярно к кривошипу в сторону его вращения. Скорость точки А2 совпадает со скоростью точки A1 и на плане скоростей вектор ра2 совпадает с вектором ра1.
В группе
Ассура (2,3) определяем сначала скорость V![]() точки А3 кулисы 3. Рассматривая
движение точки А3 сначала по отношению к центру шарнира А1
а затем по отношению к точке В, запишем два векторных уравнения:
точки А3 кулисы 3. Рассматривая
движение точки А3 сначала по отношению к центру шарнира А1
а затем по отношению к точке В, запишем два векторных уравнения: ![]()
![]()
Скорость
скольжения ![]() точки А3
кулисы 3 относительно центра A1 шарнира, направлена параллельно АВ.
точки А3
кулисы 3 относительно центра A1 шарнира, направлена параллельно АВ. ![]() - относительная
скорость точки А3 во вращательном движении звена 3 вокруг точки В.
Эта скорость направлена перпендикулярно к АВ. Точка В неподвижна,
следовательно
- относительная
скорость точки А3 во вращательном движении звена 3 вокруг точки В.
Эта скорость направлена перпендикулярно к АВ. Точка В неподвижна,
следовательно ![]() .
.
При графическом решении через точку а1 проводим прямую параллельно АВ, а через полюс р проводим прямую, перпендикулярно к АВ. Точка пересечения этих прямых определяет положение конца а3 вектора ра3 абсолютной скорости точки А3 кулисы.
![]()
Положение точки с3
на отрезке pa3или его продолжении определим по теореме
подобия, используя соотношение: 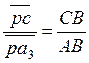 , где
, где ![]()
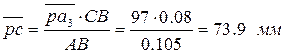
Из точки Р плана
скоростей проведем направление вектора Vcперпендикулярно
звену ВС в сторону ω3. На этом луче откладываем длину
вектора ![]() .
.
![]()
Переходим
к группе (4,5). Для определения скорости точки D
напишем два векторных уравнения: ![]()
![]() и
и ![]() , где: Do- точка неподвижной направляющей О.
Скорость точки С определена ранее; скорость точки Doизвестна она равна нулю, так как
принадлежит неподвижной направляющей. Векторы относительных скоростей не
известны по величине, но известны по направлению.
, где: Do- точка неподвижной направляющей О.
Скорость точки С определена ранее; скорость точки Doизвестна она равна нулю, так как
принадлежит неподвижной направляющей. Векторы относительных скоростей не
известны по величине, но известны по направлению.
В соответствии с
первым векторным уравнением через точку с на плане скоростей проводим
прямую, перпендикулярную звену DC.
Это будет линия
вектора![]()
![]() .
Согласно второму векторному уравнению через точку do, совпадающую
.
Согласно второму векторному уравнению через точку do, совпадающую
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.