Прямая и двойственная задачи тесно связаны: решение прямой задачи полностью определяет решение двойственной. Эта связь имеет принципиальное значение—она позволяет построить алгоритмы решения каждой задачи и дать переменным двойственной задачи важную экономическую трактовку. Так, в производственной задаче линейного программирования компоненты решения двойственной задачи можно рассматривать как оценки производственных ресурсов, объемы которых ограничены сверху, и производимых продуктов, количества которых ограничены снизу. Если в данной экономической системе установить именно такие оценки, то, с одной стороны, упрощается принятие экономически обоснованных решений, с другой—предприятия будут стимулироваться такими оценками к выполнению оптимального плана, установленного для них вышестоящим органом.
Заметим, что в некоторых частных случаях (например, одноцелевом назначении ресурсов) оценки, полученные из двойственной задачи, совпадают по структуре (а при выборе соответствующего масштаба и по величине) с описанными в 11.1. дифференциальными затратами, учитывающими обратные связи
273
в системе. В общем случае, когда ресурсы имеют много назначений, их дефицитность определяется величиной двойственных оценок в оптимальном плане. Они показывают, насколько изменится экстремум целевой функции при малом приращении соответствующего ресурса. Аналогичные трактовки могут быть даны и продуктам, рассчитанным из оптимального плана.
Обратимся к примерам некоторых типовых задач синтеза оптимального плана и определения оценок его ресурсов и продуктов.
1. Представим двумерную статическую балансовую модель оптимизации в виде следующей системы уравнений и неравенств (см. 10.4.):
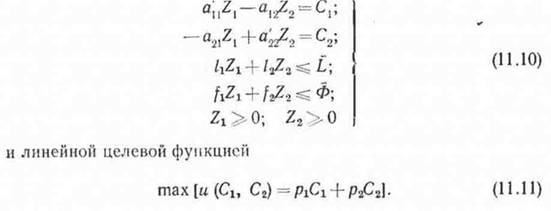
Здесь L и Ф—ограничения сверху на затраты труда и использование основных производственных фондов; р\ и рч—заданные коэффициенты компонент потребления, например цены или меры предпочтения каждого из них; а'^ -= 1—а^. Функция потребления и(С\,Сч} построена в предположении взаимозаменяемости благ Ci и Са и представляет собой их линейную комбинацию. Задача оптимизации (прямая) заключается в отыскании таких интенсивностей потребления, при которых максимизируется функция (11.11) и выполняются ограничения (11.10). Запишем ограничения (11.10) в виде;
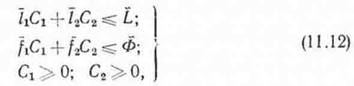
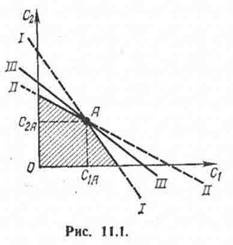
где h и ft— коэффициенты соответствующих полных затрат. Воспользуемся графической интерпретацией (11.12) для отыскания интересующих нас показателей. На рис. 11.1 заштрихованный многоугольник, образованный прямыми_1—I, II—II и осями координат, т. е. Ci=0; Сд==0; 7iCi+^2==^(I—I)i /id + ^2 = Ф (I I — II) есть область допустимых решений задачи. При выбранных нами значениях pi и рч прямая Ill—Ill, вдоль
274
которой м=тах, проходит через точку А. Координаты А соответствуют условному экстремуму целевой функции. Их можно вычислить из уравнений (11.12) как координаты точки пересечения прямых I—I и II—II:
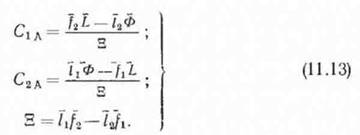
Следовательно, максимум целевой функции определяется так:
![]()
По найденным значениям c)a и Счл легко вычислить значения показателей Z^ и Zg в оптимальном балансе.
Предположим, что лимитирующие значения факторов производства изменились на малые величины AL и ЛФ. Тогда целевая
функция получит малое приращение в окрестности точки А, определяемое соотношением

Частные производные Э^ и Эф— предельные оценки эффективности факторов производства в точке оптимума — оценки оптимального плана. Они показывают, насколько изменяется значение экстремума целевой функции при малых изменениях ограничений на лимитирующие факторы производства. Очевидно, что оценки факторов, не лимитирующих производство, т. е. имеющихся в избытке сравнительно с потребностями оптимального плана, равны нулю. В нашем случае:
![]()
причем их размерность определяется размерностью параметров pi и р2 в целевой функции, каждый из которых играет роль оценю! соответствующей компоненты в потребительском наборе.
275
Оценки оптимального плана могут быть получены также из двойственной задачи линейного программирования, которая в рассматриваемом случае запишется так:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.