Проблема устойчивости нелинейных систем и методы её решения. Постановка общей задачи исследования устойчивости движений динамических систем по Ляпунову, страница 6

функция Ляпунова предлагается того же вида: .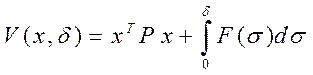

Система описывается  уравнениями:

Объект: 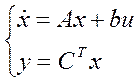.    Нелинейность   :    

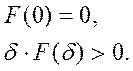
(Нелинейность находится в I и III квадрантах).       .

После выполнения аналогичных преобразований получают неравенство: , где , а матрица Р есть решение соответствующего уравнения Ляпунова . Полученное неравенство характеризует коэффициент усиления системы (глубину обратной связи), при котором система остается устойчивой.

В обоих случаях получили, что условия устойчивости не зависят от конкретного вида нелинейности и начальных условий. Устойчивость, не зависящая от начальных условий, как уже было отмечено ранее, называется устойчивостью системы в целом, а не зависящая от конкретного вида нелинейности – абсолютной устойчивостью.

Нелинейность φ(σ) по Лурье – это не есть какая-то определенная нелинейная статическая функция.

Таким образом по определению Лурье рассматриваются нелинейности j(·), принадлежащие классу "0 - К".

У функции j(·) есть одно дополнительное свойство:  j(0)=0, то есть она должна начинаться с нуля (проходить через нуль).

Введение классов нелинейных функций привело к тому, что условия "достаточности" Ляпунова "в большом" потребовали доопределения возможности раширения пространства G[V(t)] до бесконечности.

Для систем с нелинейностями, принадлежащими классу «0-k», это было проделано в 1967 году двумя советскими учеными Е.П. Барбашиным и Н.Н. Красовским.

Появилась возможность исследовать устойчивость не отдельных динамических процессов, а устойчивость самих систем, с нелинейностями, принадлежащими классу «0-k», и не "в большом", а "в целом". Такая асимптотическая устойчивость НСАУ "в целом" получила название абсолютная устойчивость НСАУ.

Теперь изменилось и понятие "пространства G[V(t)]". Параметры V(t) определяются коэффициентами положительно определеннойматрицы Р в выражении для функции Ляпунова.  Сама матрица есть модель линейной части ЭМС (однозначно определяется параметрами системы). Если изменения параметров ЭМС будут ограничены предельно допустимыми для данного технического устройства величинами *⁾ (напряжения, тока, угловой скорости и др.), то будет ограничена по величине и матрица Р. Следовательно, ограничены V(t) и пространство G[V(t)], охватывающее эти координаты. Тогда устойчивость НСАУ будет определяться "в большом". Однако, если коэффициенты матрицы Р можно увеличивать, не теряя её свойства положительной определенности, то растут V(t) и пространство G[V(t)]. Тогда устойчивость НСАУ будет определяться "в целом".

На основе прямого метода Ляпунова разработаны различные частотные критерии абсолютной устойчивости НСАУ с использованием V-функций в форме Лурье. Могут быть и другие формы, например, форма V-функции, предложенная частотной теоремой Калмана-Якубовича. Первая форма используется в критерии румынского ученого Василя Михая Пóпова, а вторая в круговом критерии устойчивости В.А. Якубовича.

Круговой  критерий абсолютной экспоненциальной устойчивости 

В. А. Якубовича

Владимир Андреевич Якубович ввел понятия необходимости наличия "локальной " или "интегральной" связей для "секторных "нелинейностей, принадлежащих классу «k₁-k₂» (1963г.).

Владимир Андреевич Якубович (род. в 1926г.) известный российский математик, профессор,  заведующий кафедрой теоретической кибернетики Санкт-Петербургского ГУ, член-корреспондент Российской Академии Наук, академик Российской Академии Естественных Наук,  работающий в области создания методов теории управления.