Проблема устойчивости нелинейных систем и методы её решения. Постановка общей задачи исследования устойчивости движений динамических систем по Ляпунову, страница 11

Поэтому логично принять, что луч  является верхней границей сектора "0 - К". Ранее мы уже проделали такую операцию с нижней границей сектора, положив .

Пример 1. Вычислим к_пр нелинейности φ(σ), если ЛЧ системы имеет такие данные: Примем:  Коэффициент линеаризации нелинейностей φ(σ)=k. Тогда, к_пр= k* k_л. Найдем ПФ замкнутой линеаризированной НСАУ: 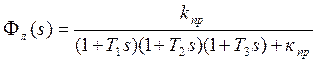. Вычислим  коэффициенты полинома знаменателя ; .a₀=0,1c³, a₁=0,8c², a₂=1,7c, a₃=(1+ к_пр).

По критерию Гурвица найдем: к_пр=12,6.  На рисунке проведен (красный) луч с коэффициентом   к_пр=12,6 (при к_л=1). Таким образом, все три нелинейности φ₁ (σ) -  φ₃ (σ) попадают в класс 0-К_пр с заданной ПФ линейной части системы К_л(s). Если же будем иметь к_л=10, то к_пр=1,26  и  попадание φ₁ (σ) в класс 0-К становится  сомнительным

Применение критерия Пòпова для оценки абсолютной устойчивости  нелинейных систем с гистерезисными характеристиками нелинейности

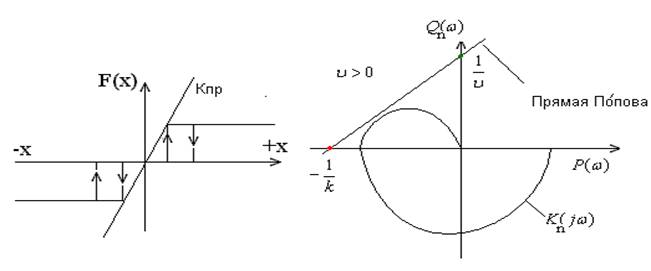
Пусть имеем в НСАУ статическую двузначную нелинейность с "опережающей" гистерезисной характеристикой, (то есть площадь петли гистерезиса будем считать положительной), ЛЧ остается та же самая.

 

Борис Николаевич Наумов (известный специалист в теории управления нелинейными системами) предлагает брать  при опережающем гистерезисе  (верхний рисунок), а при отстающем гистерезисе  (рисунок ниже).

 

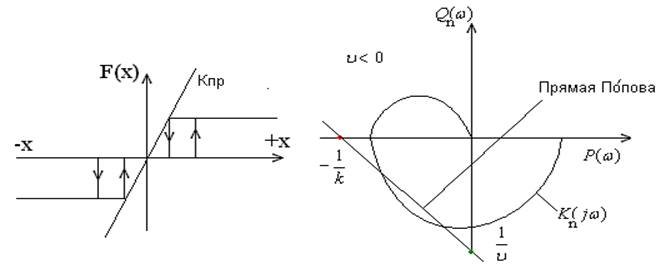Система с нелинейностью, обладающей отстающим гистерезисом, (при такой же ЛЧ) будет менее устойчива. (Смотри нижний рисунок). Это можно избежать, лишь уменьшив коэффициент передачи К_л(s).

Рассмотренные варианты применения критерия Пòпова пригодны только для оценки моделей нелинейных систем с устойчивыми статическими  ЛЧ.

При наличии астатических или неустойчивых статических линейных частей в нелинейных системах их устойчивость в классе нелинейностей "0 - К" оценивается по такой же методике, как и при "круговом " критерии.

Применение критерия Пòпова для оценки абсолютной устойчивости

 нелинейных систем с нейтральной (астатической) и неустойчивой

 линейной частью

Рассмотренные варианты применения критерия Пòпова пригодны только для оценки моделей нелинейных систем с устойчивыми статическими  ЛЧ.

При наличии астатических или неустойчивых статических линейных частей в нелинейных системах их устойчивость в классе нелинейностей "0 - К" оценивается по такой же методике, как и при "круговом " критерии Якубовича.

Сравнение критериев абсолютной устойчивости Якубовича и Пòпова

По круговому критерию Якубовича исследуются модели НСАУ с нелинейностями, принадлежащими классу "К₁-К₂". А по критерию Пòпова рассматривается класс "0-К".

1. В круговом критерии Якубовича, если к₁ = 0, то (формально) можно считать к₂ = к, где "к" граничное значение сектора в частотном критерии Пòпова. Однако, через точку, расположенную на оси абсцисс с координатой , по критерию Якубовича проводим вертикальную прямую "границы запретной зоны", а по критерию Пòпова наклонную прямую. Таким образом, для этих критериев запретные зоны для АФХ линейных частей НСАУ совпадают.

2. Вместе с тем в критерии Пòпова необходимо применять приведенную АФХ линейной части системы: , а в круговом критерии Якубовичаобычную АФХ разомкнутой ЛЧ  . Поскольку для ЛЧ системы по этим критериям абсолютной устойчивости строятся разные АФХ, то результатов могут быть получены только по завершению исследования устойчивости одной и той же конкретной НСАУ различными методами.

Резюме. По сути дела, мы закончили рассмотрение проблемы устойчивости отдельных свободных движений в НСАУ и абсолютной устойчивости систем в целом. Но скорректированный вариант текста лекции существенно больше "прочитанного" её варианта. Это связано с тем, что теперь все теоретические положения подкреплены конкретными примерами, которые потребовали значительных описаний и математических пояснений. Без этих примеров, даже поверхностно, разобраться во всех аспектах проблемы сложно.