Каб знайсці найбольшае і найменшае значэнні непарыўнай
функцыі ![]() на адрэзку
на адрэзку ![]() , трэба
вызначыць усе яе крытычныя пункты
, трэба
вызначыць усе яе крытычныя пункты ![]() і
выбраць найбольшае і найменшае значэнні сярод лікаў
і
выбраць найбольшае і найменшае значэнні сярод лікаў ![]() ,
, ![]() ,
, ![]() .
.
Прыклад 2. Знайсці найбольшае і найменшае значэнні
функцыі ![]() на адрэзку
на адрэзку![]() .
.
►Паводле гэтага правіла знойдзем ![]() і
стацыянарныя пункты
і
стацыянарныя пункты ![]() .
Сярод значэнняў
.
Сярод значэнняў ![]() ,
, ![]() ,
, ![]() ,
, ![]() знойдзем
найбольшае і найменшае. Адкуль вынікае, што
знойдзем
найбольшае і найменшае. Адкуль вынікае, што
![]() . ◄
. ◄
Даследаванне функцыі дзеля пабудовы яе графіка можна праводзіць па наступнай схеме:
1. Знайсці абсяг вызначэння функцыі. Высветліць, ці з’яўляецца яна цотнай, няцотнай, перыядычнай. Знайсці пункты перасячэння графіка функцыі з восямі каардынатаў, прамежкі, дзе значэнні функцыі дадатныя, адмоўныя.
2. Знайсці асімптоты графіка функцыі і аднабаковыя ліміты ў межавых пунктах абсягу вызначэння.
3. Вылічыць першую вытворную функцыі і вызначыць пункты экстрэ-муму, а таксама прамежкі яе нарастання і спадання.
4. Вылічыць вытворную другога парадку і вызначыць пункты перагіну графіка функцыі, прамежкі выпукласці.
Прыклад 3. Даследаваць функцыю ![]() .
.
►Правядзём даследаванне функцыі паводле пададзенай схемы.
1. Абсяг вызначэння функцыі ёсць уся рэчаісная
вось, акрамя пункта ![]() . Абцысы
пунктаў перасячэння графіка функцыі з восямі каардына-таў ёсць
. Абцысы
пунктаў перасячэння графіка функцыі з восямі каардына-таў ёсць ![]() ,
, ![]() . Функцыя
дадатная на
. Функцыя
дадатная на ![]() і адмоўная на
і адмоўная на
![]() .
.
2. Знойдзем асімптоты графіка функцыі. Дастасуем
формулу Маклёрэна для экспаненты, пасля чаго атрымаем ![]()
![]() . Адкуль
вынікае, што асімптотай графіка функцыі будзе прамая
. Адкуль
вынікае, што асімптотай графіка функцыі будзе прамая ![]() . Каб знайсці
вертыкальныя асімптоты, вылічым
. Каб знайсці
вертыкальныя асімптоты, вылічым 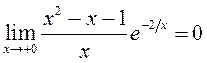 і
і
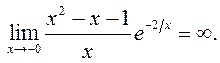 Такім чынам,
існуе вертыкальная асімптота
Такім чынам,
існуе вертыкальная асімптота ![]() ,
да якой графік функцыі набліжаецца злева.
,
да якой графік функцыі набліжаецца злева.
3. Вылічым першую вытворную 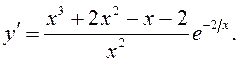 Прыраўняем
яе да нуля і знойдзем стацыянарныя пункты
Прыраўняем
яе да нуля і знойдзем стацыянарныя пункты ![]() ,
, ![]() ,
, ![]() . Даследуем
знакі вытворнай, адкуль маем, што на
. Даследуем
знакі вытворнай, адкуль маем, што на ![]() ,
і
,
і ![]() функцыя
спадае, а на
функцыя
спадае, а на ![]() ,
, ![]() ,
, ![]() – нарастае.
А гэта значыць, што
– нарастае.
А гэта значыць, што ![]() –
пункт максімуму, а
–
пункт максімуму, а ![]() ,
, ![]() – пункты
мінімуму, прычым
– пункты
мінімуму, прычым ![]()
![]()
![]()
4)Вылічым другую вытворную 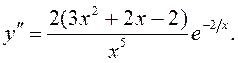 У пунктах
У пунктах ![]() ,
, ![]() другая
вытворная мае нулявое значэнне. На
другая
вытворная мае нулявое значэнне. На ![]() функцыя
выпуклая ўніз, паколькі
функцыя
выпуклая ўніз, паколькі ![]() ,
а на
,
а на ![]() і
і ![]() – выпуклая
ўверх, таму што
– выпуклая
ўверх, таму што ![]() .
Адкуль вынікае, што пункты
.
Адкуль вынікае, што пункты ![]() і
і
![]() з’яўляюцца
пунктамі перагіну. ◄
з’яўляюцца
пунктамі перагіну. ◄
3.117.
Знайдзіце прамежкі
нарастання і спадання функцый
1) ![]() 2)
2) ![]() 3)
3) ![]()
4) ![]() 5)
5)
![]() 6)
6)
![]()
7) ![]() 8)
8) ![]() 9)
9) ![]() 10)
10)![]() 11)
11)![]() 12)
12)![]()
3.118.
Пры якіх значэннях
параметра ![]() функцыя
нарастае на ўсёй восі:
1)
функцыя
нарастае на ўсёй восі:
1) ![]() 2)
2)
![]() 3)
3) ![]() 4)
4) ![]() ?
?
3.119. Знайдзіце прамежкі нарастання функцыі,
зададзенай парамет-рычна:
1) 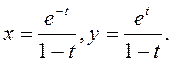 2)
2) ![]()
3.120. Дакажыце, што нарастальная дыферэнцавальная функцыя мае не-адмоўную вытворную.
3.121. Дакажыце, што дыферэнцавальная строга
нарастальная на ![]() функцыя
мае прынамсі адзін пункт, дзе
функцыя
мае прынамсі адзін пункт, дзе ![]() .
.
3.122.
Знайдзіце экстрэмумы
наступных функцый:
1) ![]() 2)
2) ![]() 3)
3) ![]()
4) ![]() 5)
5) ![]() 6)
6)![]() ;
;
7)![]() 8)
8) ![]()
9) ![]() 10)
10) ![]() 11)
11)
![]() 12)
12) ![]() 13)
13)
![]() 14)
14)
![]() 15)
15) ![]() 16)
16)
![]() 17)
17)
![]() 18)
18) ![]()
![]() 19)
19)
![]()
![]()
3.123.
Знайдзіце экстрэмумы
функцый, зададзеных няяўна.
1) ![]() 2)
2) ![]()
3.124.
Даследуйце на
экстрэмум функцыі, зададзеные параметрычна.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4)
![]()
3.125.
Дакажыце праўдзівасць
наступных няроўнасцяў.
1) ![]()
![]() 2)
2) ![]()
![]() 3)
3)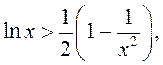
![]() 4)
4) ![]()
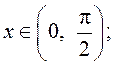 5)
5) ![]()
![]() 6)
6)![]()
![]() 7)
7) ![]()
![]() 8)
8) ![]()
3.126.
Высветліце, ці
распаўсюджваецца на рэчаісныя значэнні ![]() няроў-насць
Бэрнулі
няроў-насць
Бэрнулі ![]() , праўдзівая
для натуральных
, праўдзівая
для натуральных ![]() .
.
3.127.
Знайдзіце найбольшае і
найменшае значэнні функцый на дадзеным прамежку:
1)![]() 2)
2)![]() 3)
3)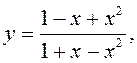
![]() 4)
4)![]()
![]() 5)
5)![]() ,
, ![]() 6)
6)![]() 7)
7)![]() 8)
8)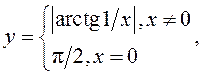
![]() 9)
9)![]()
![]() 10)
10)![]()
3.128.
Знайдзіце пункты
перфгіну і інтэрвалы выпукласці функцый:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() 5)
5) ![]() 6)
6)
![]() 7)
7) ![]() 8)
8) ![]() 9)
9) ![]() 10)
10)
![]() 11)
11)
![]() 12)
12) ![]()
3.129.
Знайдзіце пункты
перагіну графіка функцыі, зададзенай у пара-метрычнай форме:
1) ![]() 2)
2)
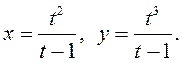
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.