3.92.
Знайдзіце:
1) 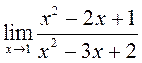 ; 2)
; 2) 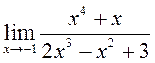 ; 3)
; 3)
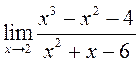 ;
4)
;
4) 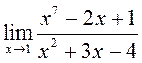 ; 5)
; 5) 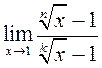 ,
, ![]() ,
,![]() ; 6)
; 6)  ,
7)
,
7) ![]() ; 8)
; 8)
![]() ; 9)
; 9) ![]() ;
10)
;
10) 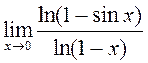 ; 11)
; 11) 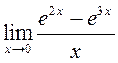 ; 12)
; 12)
![]() ;
13)
;
13) 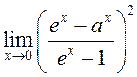 ,
,![]() ; 14)
; 14) 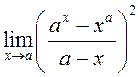 ,
,![]() ,
, ![]() ; 15)
; 15)![]() ; 16)
; 16) 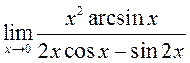 ; 17)
; 17) 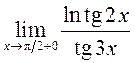 ;
18)
;
18) ![]() ; 19)
; 19) ![]() ; 20)
; 20)
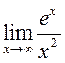 ;
21)
;
21) 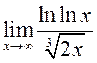 ; 22)
; 22) ![]() ; 23)
; 23) 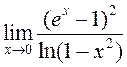 .
.
3.93.
Знайдзіце ліміты, папярэдне
пераўтвараючы выразы да патрэбнага выгляду
1)![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() .
.
3.94.
Знайдзіце
1 )![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ,
,![]() ,
, ![]() .
.
3.95.
Знайдзіце ліміты пры
дапамозе формулы ![]() :
1)
:
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4) ![]() ;
5)
;
5) ![]() ; 6)
; 6)
![]() ; 7)
; 7) ![]() ; 8)
; 8)
![]() ;
9)
;
9) ![]() ; 10)
; 10) ![]() ; 11)
; 11)
![]() ; 12)
; 12) ![]() ;
13)
;
13) ![]() ; 14)
; 14)
![]() ; 15)
; 15)
 ;
16)
;
16) ![]()
3.96.
Пакажыце, што
наступныя ліміты не могуць быць вылічаны з дапамогай правіла Лёпіталя.
Знайдзіце гэтыя ліміты
1) ![]() 2)
2) 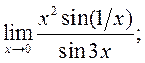 3)
3) ![]() 4)
4) 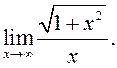
Няхай функцыя ![]() у ваколлі
пункта
у ваколлі
пункта ![]() мае вытворныя
да
мае вытворныя
да ![]() -га парадку
ўключна і няхай існуе
-га парадку
ўключна і няхай існуе ![]() .
Тады мае месца формула Тэйлара:
.
Тады мае месца формула Тэйлара:
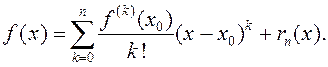 (3.22)
(3.22)
Паліном 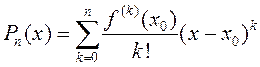 называецца
паліномам Тэйлара функцыі
называецца
паліномам Тэйлара функцыі ![]() у пункце
у пункце ![]() , функцыя
, функцыя ![]() называецца рэшткавым
складнікам
называецца рэшткавым
складнікам ![]() - га
парадку формулы Тэйлара. Пры дадзеных умовах рэшткавы складнік можна запісаць у
форме Пэана
- га
парадку формулы Тэйлара. Пры дадзеных умовах рэшткавы складнік можна запісаць у
форме Пэана ![]() .
Калі
.
Калі ![]() = 0, то
формула Тэйлара называецца формулай Маклёрэна.
= 0, то
формула Тэйлара называецца формулай Маклёрэна.
Формулы Маклёрэна для асноўных элементарных функцый:
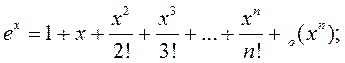
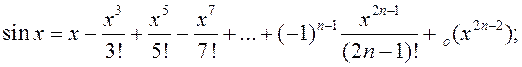
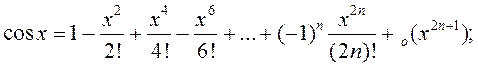
![]()
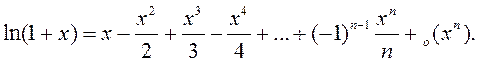
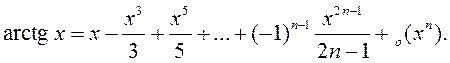
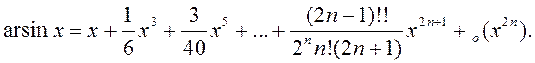
Калі функцыя ![]() у
ваколлі пункта
у
ваколлі пункта ![]() мае
вытворныя да
мае
вытворныя да ![]() - га парадку
ўключна, то для кожнага пункта
- га парадку
ўключна, то для кожнага пункта ![]() з
дадзенага ваколля знойдзецца паміж пунктамі
з
дадзенага ваколля знойдзецца паміж пунктамі ![]() і
і ![]() пункт
пункт ![]() такі, што
такі, што 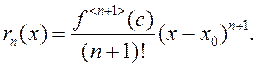 Такая форма
рэшткавага складніка носіць назву рэшткавага складніка ў форме Лягранжа.
Такая форма
рэшткавага складніка носіць назву рэшткавага складніка ў форме Лягранжа.
Прыклад 1. Раскласці паводле формулы Маклёрэна функцыю ![]() з дакладнасцю
да
з дакладнасцю
да ![]() .
.
►Для развязання задачы дастасуем формулу (3.22) пры ![]() =0. Паколькі
функцыя
=0. Паколькі
функцыя ![]() няцотная, то
дастаткова знайсці вытворныя функцыі
няцотная, то
дастаткова знайсці вытворныя функцыі ![]() да
пятага парадка уключна:
да
пятага парадка уключна:
![]()
![]()
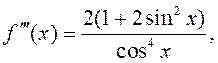
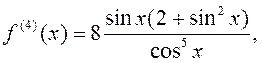
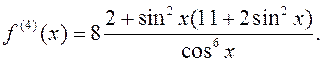
Адсюль
маем ![]()
![]()
![]()
![]()
![]()
Таму
![]()
Прыклад 2. Раскласці паводле формулы Маклёрэна функцыю ![]() з дакладнасцю
да
з дакладнасцю
да ![]() .
.
►Для развязання задачы дастасуем вядомыя расклады
функцый ![]() ,
, ![]() . Расклад
сінуса дастаткова ўзяць з дакладнасцю да
. Расклад
сінуса дастаткова ўзяць з дакладнасцю да ![]() , таму што
, таму што 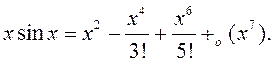
Паколькі 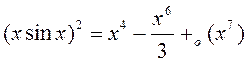 ,
, ![]() і
і ![]() для
для ![]() , то ў
раскладзе функцыі
, то ў
раскладзе функцыі ![]() ,
дзе
,
дзе ![]() , дастаткова
ўзяць чатыры першыя складнікі:
, дастаткова
ўзяць чатыры першыя складнікі:
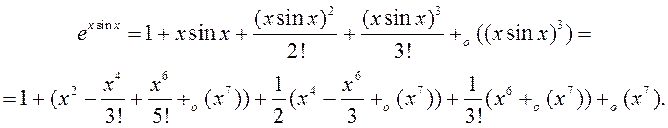
Адсюль маем 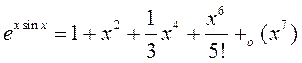 .◄
.◄
Прыклад 3. Знайсці ![]()
►Раскладзем функцыі ![]() і
і ![]() паводле
формулы Маклёрэна
паводле
формулы Маклёрэна 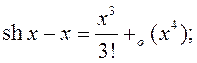
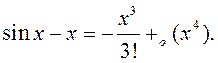 Адсюль
Адсюль
 ◄
◄
Прыклад 4. З дакладнасцю да ![]() вылічыць
вылічыць ![]() .
.
►Паводле формулы Маклёрэна для сінуса маем 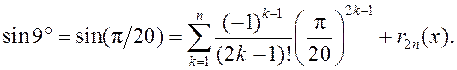 З формулы Лягранжа
для рэшткавага складніка вынікае, што
З формулы Лягранжа
для рэшткавага складніка вынікае, што 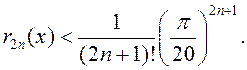 З няроўнасці
З няроўнасці ![]() маем, што
маем, што ![]() . Каб вылічыць
. Каб вылічыць
![]() з неабходнай
дакладнасцю, у формуле Маклёрэна дастаткова ўзяць першыя тры складнікі
з неабходнай
дакладнасцю, у формуле Маклёрэна дастаткова ўзяць першыя тры складнікі 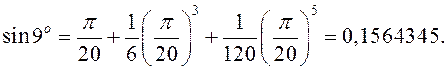 ◄
◄
3.97.
Раскладзіце паводле
формулы Маклёрэна з дакладнасцю да ![]() наступныя
функцыі:
1)
наступныя
функцыі:
1) 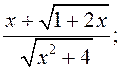 2)
2)  3)
3) ![]() 4)
4) 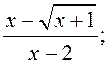 5)
5)![]() 6)
6)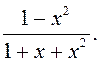
3.98.
Раскладзіце паводле
формулы Тэйлара з дакладнасцю да ![]() у
ваколлі пункта
у
ваколлі пункта ![]() наступныя
функцыі:
1)
наступныя
функцыі:
1) ![]()
![]() ; 2)
; 2) ![]()
![]() ;
3)
;
3) ![]()
![]() ;
4)
;
4) 
![]() .
.
3.99.
Знайдзіце першыя ![]() ненулявых
складнікаў раскладу паводле формулы Маклёрэна наступных функцый:
1)
ненулявых
складнікаў раскладу паводле формулы Маклёрэна наступных функцый:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() 5)
5) ![]() 6)
6) ![]()
3.100.
Знайдзіце расклад
паводле формулы Маклёрэна наступных функцый з дадзеным рэшткавым складнікам ![]() :
1)
:
1)![]()
![]() ; 2)
; 2)![]()
![]() ; 3)
; 3)![]()
![]() ; 4)
; 4)![]()
![]() ;
5)
;
5)![]()
![]() ; 6)
; 6)![]()
![]() ; 7)
; 7)![]()
![]() ; 8)
; 8)![]()
![]() .
.
3.101.
Раскладзіце паводле
формулы Тэйлара ў ваколлі пункта ![]() з
дадзеным рэшткавым складнікам
з
дадзеным рэшткавым складнікам ![]() :
1)
:
1) ![]() 2)
2) ![]() – няцотны; 3)
– няцотны; 3)
![]() 4)
4) ![]()
![]() ; 5)
; 5) ![]() 6)
6)
![]()
3.102. Раскладзіце функцыю ![]() паводле
формулы Маклёрэна. Для гэтага спачатку знайдзіце расклад функцыі
паводле
формулы Маклёрэна. Для гэтага спачатку знайдзіце расклад функцыі ![]() .
.
3.103.
Раскладзіце функцыю ![]() паводле
формулы Маклёрэна. Для гэтага спачатку знайдзіце расклад функцыі
паводле
формулы Маклёрэна. Для гэтага спачатку знайдзіце расклад функцыі ![]() .
.
3.104.
Раскладзіце функцыю ![]() паводле
формулы Маклёрэна. Для гэтага спачатку знайдзіце расклад функцыі
паводле
формулы Маклёрэна. Для гэтага спачатку знайдзіце расклад функцыі ![]() .
.
3.105.
Знайдзіце расклад
наступных функцый паводле формулы Маклё-рэна з дадзеным рэшткавым складнікам:
1) ![]()
![]() ; 2)
; 2)
![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() ; 4)
; 4) ![]() ,
, ![]() .
.
3.106.
Знайдзіце абсалютную
хібнасць набліжаных формул
1) 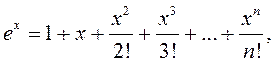
![]() ; 2)
; 2) 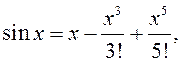
![]() ;
;
3) 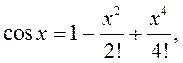
![]() ; 4)
; 4)
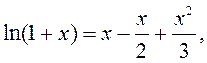
![]() ; 5)
; 5) 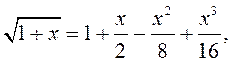
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.